【CodeTop】TOP 100 刷题 31-40

31. 二叉树中的最大路径和

题目链接：124. 二叉树中的最大路径和

题目描述

代码与解题思路

func maxPathSum(root *TreeNode) int {
    ans := math.MinInt
    var dfs func(*TreeNode) int
    dfs = func(node *TreeNode) int {
        if node == nil {
            return 0
        }
        left := dfs(node.Left)
        right := dfs(node.Right)
        ans = max(ans, left+right+node.Val)
        return max(node.Val+max(left, right), 0)
    }
    dfs(root)
    return ans
}

树形 DP，推荐学习：https://www.bilibili.com/video/BV17o4y187h1/

32. 合并区间

题目链接：56. 合并区间

题目描述

代码与解题思路

func merge(intervals [][]int) [][]int {
    sort.Slice(intervals, func(i, j int) bool {
        return intervals[i][0] < intervals[j][0]
    })
    res := [][]int{}
    pre := intervals[0]
    for i := 1; i < len(intervals); i++ {
        cur := intervals[i]
        if pre[1] < cur[0] { // 区间不重合了, 追加到 res 数组
            res = append(res, pre)
            pre = cur
        } else { // 区间重合, 扩大区间范围
            pre[1] = max(cur[1], pre[1])
        }
    }
    res = append(res, pre) // 剩下最后一个没法合并的区间, 直接追加
    return res
}

画图模拟即可，顺便学习一下如何排序二维数组：

sort.Slice(intervals, func(i, j int) bool {
    return intervals[i][0] < intervals[j][0]
})

33. 编辑距离

题目链接：72. 编辑距离

题目描述

代码与解题思路

func minDistance(word1 string, word2 string) int {
    n, m := len(word1), len(word2)
    // 创建 dp 数组
    dp := make([][]int, n+1)
    for i := 0; i < len(dp); i++ {
        dp[i] = make([]int, m+1)
    }
    // 初始化
    for i := 0; i <= n; i++ {
        dp[i][0] = i
    }
    for i := 0; i <= m; i++ {
        dp[0][i] = i
    }
    // 填表
    for i, v1 := range word1 {
        for j, v2 := range word2 {
            if v1 == v2 {
                dp[i+1][j+1] = dp[i][j]
            } else {
                dp[i+1][j+1] = min(min(dp[i+1][j], dp[i][j+1]), dp[i][j])+1
            }
        }
    }
    return dp[n][m]
}

dp 问题的核心就是状态转移方程的推导，通过分类讨论题目要求，我们能得出有这几种情况：

1. 两个字母相同，不需要修改 dp[ i+1 ][ j+1 ] = dp[ i ][ j ]
2. 两个字母不同分三种情况：
   1. word1 缺失，只需要进行一个删除操作即可 dp[ i+1 ][ j ] + 1
   2. word2 缺失，只需要进行一个删除操作即可 dp[ i ][ j+1 ] + 1
   3. word1 和 word2 字母不相同，进行替换操作即可 dp[ i+1 ][ j+1 ] + 1

最后取第二种情况的最小值即可，因为要求最少的操作次数

最后就是初始化 dp 数组，从左往右，从上往下按顺序填表

省流：熟练的默写动态规划的套路罢了，到底懂没懂不好说

34. 二叉树的中序遍历

题目链接：94. 二叉树的中序遍历

题目描述

代码与解题思路

先来个递归解法：

func inorderTraversal(root *TreeNode) (ans []int) {
    var inorder func(*TreeNode)
    inorder = func(root *TreeNode) {
        if root == nil {
            return
        }
        inorder(root.Left)
        ans = append(ans, root.Val)
        inorder(root.Right)
    }
    inorder(root)
    return ans
}

非递归：

// 记住中序遍历顺序：左根右
func inorderTraversal(root *TreeNode) (ans []int) {
    st := list.New()
    cur := root
    for cur != nil || st.Len() > 0 {
        if cur != nil { // 找最左节点
            st.PushBack(cur)
            cur = cur.Left
        } else { // 栈顶是最左节点了
            cur = st.Remove(st.Back()).(*TreeNode)
            ans = append(ans, cur.Val) // 取值
            cur = cur.Right // 找右
        }
    }
    return ans
}

我们来根据代码梳理一下他的流程

1. 将当前节点入栈，然后一直往左遍历直到走到 nil
2. 走到 nil 之后，上一个节点，也就是栈顶的元素就是最左节点，输出到 ans然后往右遍历一步，持续这个三步循环

这三步模拟的就是 “左根右” 的遍历方式，刚好也是三步，找到最左，取根，找右，循环往复，就能完成中序遍历了。

迭代算法确实不太好想，但是上手模拟一遍还是比较好理解的。

35. 最长公共子序列

题目链接：1143. 最长公共子序列

题目描述

代码与解题思路

func longestCommonSubsequence(text1 string, text2 string) int {
    n, m := len(text1), len(text2)
    dp := make([][]int, n+1)
    for i := 0; i < n+1; i++ {
        dp[i] = make([]int, m+1)
    }
    for i, v1 := range text1 {
        for j, v2 := range text2 {
            if v1 == v2 {
                dp[i+1][j+1] = dp[i][j] + 1
            } else {
                dp[i+1][j+1] = max(dp[i+1][j], dp[i][j+1])
            }
        }
    }
    return dp[n][m]
}

这道题需要注意的是，子序列和子数组，子数组必须是连续的，而子序列不一定。所以子序列相关的题目是经典的动态规划类型题目，所以我们首先分析题目然后写出状态转移方程：

1. 如果两个字母相同，dp[ i+1 ][ j+1 ] = dp[ i ][ j ] + 1
2. 如果两个字母不相同，看看之前有没有出现过相同的子序列，继承一下最长子序列的长度：dp[ i+1 ][ j+1 ] = max(dp[ i+1 ][ j ], dp[ i ][ j+1 ])

看图：

接着就是愉快的默写，初始化 dp 数组，填表，返回。

36. 二分查找

题目链接：704. 二分查找

题目描述

代码与解题思路

func search(nums []int, target int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        mid := left+(right-left)/2
        if nums[mid] < target {
            left = mid+1
        } else if nums[mid] > target {
            right = mid-1
        } else {
            return mid
        }
    }
    return -1
}

经典二分，熟练二分的思想，思考和控制好二分的边界，那二分用起来就不困难。

37. 二叉树的右视图

题目链接：199. 二叉树的右视图

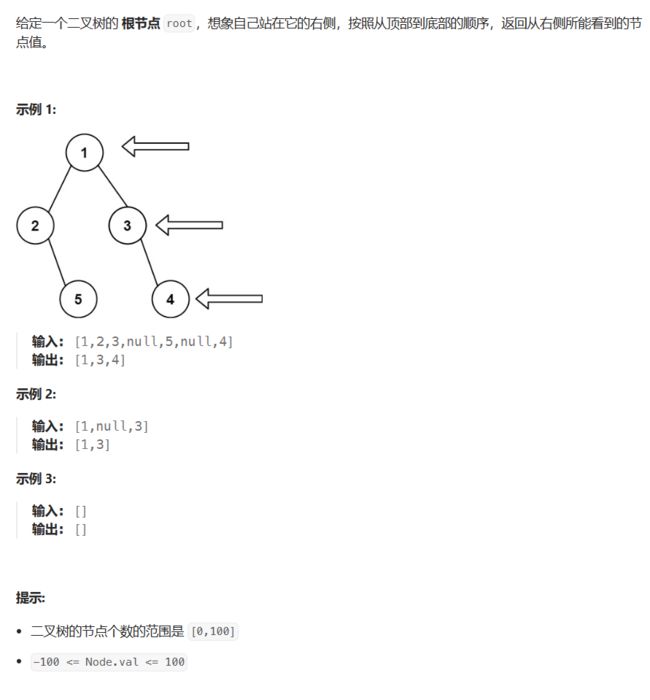
题目描述

代码与解题思路

func rightSideView(root *TreeNode) (ans []int) {
    if root == nil {
        return nil
    }
    Queue := []*TreeNode{root}
    for len(Queue) > 0 {
        n := len(Queue)
        nextQueue := []*TreeNode{}
        for n > 0 {
            cur := Queue[0]
            Queue = Queue[1:]
            if cur.Left != nil {
                nextQueue = append(nextQueue, cur.Left)
            }
            if cur.Right != nil {
                nextQueue = append(nextQueue, cur.Right)
            }
            n--
            if n == 0 {
                ans = append(ans, cur.Val)
            }
        }
        Queue = nextQueue
    }
    return ans
}

今天真是头昏了，被层序玩傻了，下次写层序遍历用土方法吧，先画图，然后对照着图的思路来写层序遍历，不要浪了，踏踏实实才是真本领，再怎么背模板总会忘记的，融会贯通才是最重要的。

38. 用栈实现队列

题目链接：232. 用栈实现队列

题目描述

代码与解题思路

type MyQueue struct {
    st1 []int
    st2 []int
}

func Constructor() MyQueue {
    return MyQueue{
        st1: []int{},
        st2: []int{},
    }
}

func (q *MyQueue) Push(x int)  {
    q.st1 = append(q.st1, x)
}

func (q *MyQueue) Pop() int {
    st1ToSt2(q)
    front := q.st2[len(q.st2)-1]
    q.st2 = q.st2[:len(q.st2)-1]
    return front
}

func (q *MyQueue) Peek() int {
    st1ToSt2(q)
    return q.st2[len(q.st2)-1]
}

func st1ToSt2(q *MyQueue) { // 抽象出数据流转操作
    if len(q.st2) == 0 {
        n := len(q.st1) // 注意, 因为后续操作会影响到 q.st1
        for i := 0; i < n; i++ {
            q.st2 = append(q.st2, q.st1[len(q.st1)-1]) 
            q.st1 = q.st1[:len(q.st1)-1]
        }
    }
}

func (q *MyQueue) Empty() bool {
    if len(q.st1) == 0 && len(q.st2) == 0 {
        return true
    }
    return false
}

这里有个需要注意的地方，就是在遍历的时候会改变 q.st1 数组的大小，所以在使用 for 循环的时候需要提前求出 n := len(q.st1) 然后使用 n，而不能直接使用 len(q.st1) 作为判断的条件

39. 删除排序链表中的重复元素 II

题目链接：82. 删除排序链表中的重复元素 II

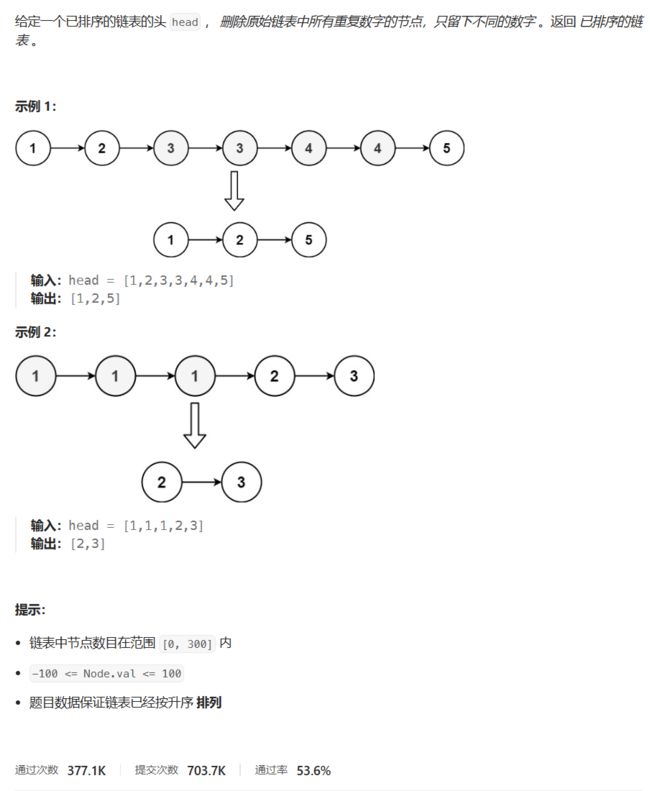
题目描述

代码与解题思路

func deleteDuplicates(head *ListNode) *ListNode {
    phead := &ListNode{Next: head}
    cur := phead // cur 一直保持在前一个节点这个相对位置
    for cur.Next != nil && cur.Next.Next != nil {
        nVal, nnVal := cur.Next.Val, cur.Next.Next.Val
        if nnVal == nVal { // 如果出现相同的情况, 就跳过重复节点
            for cur.Next != nil && cur.Next.Val == nVal {
                cur.Next = cur.Next.Next
            }
        } else {
            cur = cur.Next
        }
    }
    return phead.Next
}

这个是练习链表的基本功问题，下次遇到再重新做做，检测一下自己的链表内功。

40. 寻找两个正序数组的中位数

题目链接：4. 寻找两个正序数组的中位数

题目描述

代码与解题思路

func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
    nums1 = append(nums1, nums2...)
    sort.Ints(nums1)
    if len(nums1)%2!=0 {
        return float64(nums1[len(nums1)/2])
    }
    return float64(nums1[len(nums1)/2-1]+nums1[len(nums1)/2])/2
}

这道题比较难，所以我决定开摆，直接合并数组+排序一气呵成。