【人工智能Ⅰ】实验7：K-means聚类实验

实验7 K-means聚类实验

一、实验目的

学习K-means算法基本原理，实现Iris数据聚类。

二、实验内容

应用K-means算法对iris数据集进行聚类。

三、实验结果及分析

0：输出数据集的基本信息

参考代码在main函数中首先打印了数据、特征名字、目标值、目标值的名字，iris数据集的结果如下图所示。

【数据】

    数据共有150组，每组包含4个特征。

【特征名字】

    每组数据包含的特征为：花萼长度、花萼宽度、花瓣长度、花瓣宽度。其中sepal对应花萼，而petal对应花瓣。

【目标值】

    数据集里面共包含3种鸢尾，标签分别是0、1、2。由此可知，我们后面需要通过K-means算法聚成3类以进行分类。

【目标值的名字】

数据集里面标签分别为0、1、2的各组数据，类别分别对应setosa、versicolor、virginica。

同时，参考代码中利用show_data函数，分别画出了花萼长度和宽度的关系和花瓣长度和宽度的关系，结果如下图所示。

【Sepal花萼】

【Petal花瓣】

1：调用Kmeans进行聚类

在任务1中，需要分别对Sepal和Petal进行聚类。此处使用【sklearn】库中的KMeans封装包进行调用，选定初始的聚类数目为3，采用fit方法进行模型训练，最后得到训练标签为【kmeans_sepal.labels_】和【kmeans_petal.labels_】。整体代码如下图所示。

同时，采用head方法输出前几个数据的聚类情况，程序输出结果如下图所示。

2：绘出聚类前后的图

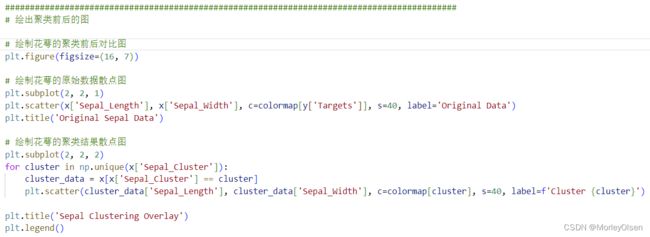
在任务2中， 我们定义了图的大小，并定义了4个子图，分别用于显示花萼聚类前、花萼聚类后、花瓣聚类前、花瓣聚类后的聚类散点图。整体代码如下图所示。

程序输出结果如下图所示。其中，Original Sepal Data对应原始花萼数据，Sepal Clustering Overlay对应聚类后的花萼数据，Original Petal Data对应原始花瓣数据，Petal Clustering Overlay对应聚类后的花瓣数据。

3：计算并输出准确率

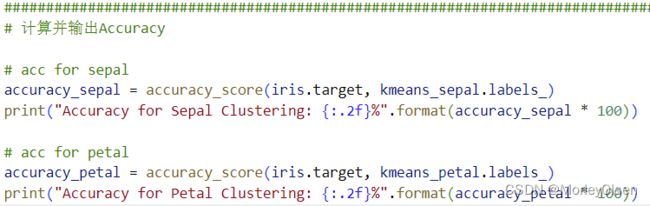
在任务3中，利用【from sklearn.metrics import accuracy_score】从评价指标中调用准确率，输入数据集本身的标签和kmeans算法聚类得到的标签，进行对比后输出准确率结果。整体代码如下图所示。

程序输出结果如下图所示。可以看到计算出来的花萼聚类的准确率为25.33%、花瓣聚类的准确率为1.33%。

通过任务2中的对比图可知，原来的标签与聚类结果的标签所对应的关系如下表所示。其中，表格中的橘色位置处均是结果标签与原始标签存在不一致的情况。因此，该准确率存在不准确的情况，只有当原始标签等于结果标签时，才能得到正确的Accuracy。同时，应该采用适合非监督学习的评价指标进行结果优劣的判断。

聚类对象	原始标签	结果标签
花萼	红	黑
	绿	绿
	黑	红
花瓣	红	黑
	绿	红
	黑	绿

4：计算并输出轮廓系数（自增）

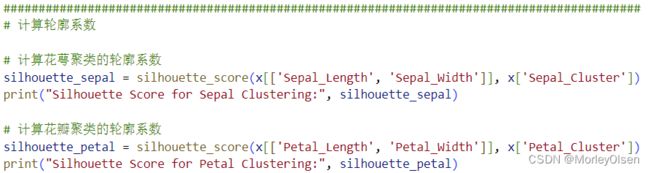
在任务4中，利用【from sklearn.metrics import silhouette_score】从评价指标中调用轮廓系数，输入数据集本身的特征值和kmeans算法聚类得到的标签，进行对比后输出轮廓系数结果。整体代码如下图所示。

程序输出结果如下图所示。可以看到计算出来的花萼聚类的轮廓系数为0.45左右、花瓣聚类的轮廓系数为0.66左右。

5：计算并输出Adjusted Rand Index（自增）

在任务5中，利用【from sklearn.metrics import adjusted_rand_score】从评价指标中调用ARI，输入数据集本身的标签和kmeans算法聚类得到的标签，进行对比后输出ARI结果。整体代码如下图所示。

 程序输出结果如下图所示。可以看到计算出来的花萼聚类的ARI为0.60左右、花瓣聚类的ARI为0.89左右。

四、遇到的问题和解决方案

问题1：每次执行时，K-means聚类算法计算出来的Accuracy均不同。

解决1：经过对比打印出的数据标签和聚类标签可知，K-means聚类算法在每次执行后给每一类分配的标签不同，只具备一定的映射关系（例如dataset中的0标签与kmeans-label中的1标签相映射，而不是与kmeans-label中的0标签对应）。但是不能保证每次代码运行后的映射关系相同，因此需要采用ARI评价指标来评估聚类的好坏。

五、实验总结和心得

1：KMeans包中可修改以下参数：n_clusters（指定要分成的簇的数量）、init（用于初始化簇中心的方法，可以选择随机初始值random，或从数据中选择初始值k-means++）、n_init（执行K均值算法的次数）、max_iter（每次迭代的最大次数）、tol（收敛的阈值）、random_state（用于确定随机种子的整数，以确保结果的可重复性）、algorithm（用于计算距离的算法，可以选择full、elkan、auto等）、precompute_distances（指定是否预先计算距离，可以加速算法的收敛）。一般来说，最重要的是确定簇的数量 n_clusters，因为它会直接影响到聚类的结果。

2：ARI用于评估聚类结果与真实标签之间的一致性，其取值范围在[-1, 1]之间，越接近1表示聚类效果越好。

3：轮廓系数用于衡量数据点与其所属簇内部的相似度和与其他簇之间的差异度，其取值范围在[-1, 1]之间。轮廓系数接近1表示数据点与其所属簇内的其他数据点非常相似，同时与其他簇的数据点差异很大，通常表示数据点被正确地分配到了合适的簇中。轮廓系数接近0表示数据点与其所属簇内部的数据点相似度与其他簇的数据点相似度差不多，通常表示数据点可能位于两个或多个簇的边界上。轮廓系数接近-1表示数据点与其所属簇内的其他数据点差异很大，但与其他簇的数据点相似度高，通常表示数据点被错误地分配到了不合适的簇中。轮廓系数可以用于选择最佳的K值，比较不同聚类算法的性能，或者评估聚类结果的质量。

4：K均值聚类的主要思想是通过迭代寻找簇中心，将数据点分配到距离最近的簇中心。在应用聚类算法之前，可以进行实验并评估聚类性能。通过可视化和指标评估，可以更好地理解数据的结构和选择合适的K值。

六、附录

（1）完整程序源代码（含注释）

各部分的任务操作在多行代码注释下构造。各段代码含有概念注释模块。

import matplotlib.pyplot as plt from sklearn import datasets from sklearn.cluster import KMeans import sklearn.metrics as sm import pandas as pd import numpy as np from sklearn.metrics import accuracy_score from sklearn.metrics import adjusted_rand_score from sklearn.metrics import silhouette_score def print_data(want_print, print_iris):     """     展示iris的数据     :return: None     """     print("iris{0}为:\n{1}".format(want_print, print_iris))     print("=" * 85)   def show_data(length, width, title):     """     画图     :param length: 长度     :param width: 宽度     :param title: 标题     :return: None     """     # 建立一个画布     plt.figure(figsize=(14, 7))     plt.scatter(length, width, c=colormap[y.Targets], s=40)     plt.title(title)     plt.show() if __name__ == '__main__':     # 导入iris数据     iris = datasets.load_iris()     # 展示iris真实数据     print_data(want_print="数据", print_iris=iris.data)     # 展示iris特征名字     print_data(want_print="特征名字", print_iris=iris.feature_names)     # 展示目标值     print_data(want_print="目标值", print_iris=iris.target)     # 展示目标值的名字     print_data(want_print="目标值的名字", print_iris=iris.target_names)     # 为了便于使用，将iris数据转换为pandas库数据结构，并设立列的名字     # 将iris数据转为pandas数据结构     x = pd.DataFrame(iris.data)     # 将iris数据的名字设为‘Sepal_Length’，‘Sepal_Width’，‘Sepal_Width’，‘Petal_Width’     x.columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width']     # 将iris目标值也转为pandas数据结构     y = pd.DataFrame(iris.target)     # 将iris目标值得名字设为‘Targets’     y.columns = ['Targets']     # 创建色板图     colormap = np.array(['red', 'lime', 'black'])     # 开始画Sepal长度和宽度的关系     show_data(length=x.Sepal_Length, width=x.Sepal_Width, title='Sepal')     # 开始画Petal长度和宽度的关系     show_data(length=x.Petal_Length, width=x.Petal_Width, title='Petal')         ###########################################################################################     # 调用Kmeans进行聚类         # for sepal     kmeans_sepal = KMeans(n_clusters=3)     kmeans_sepal.fit(x[['Sepal_Length', 'Sepal_Width']])     x['Sepal_Cluster'] = kmeans_sepal.labels_     # for petal     kmeans_petal = KMeans(n_clusters=3)     kmeans_petal.fit(x[['Petal_Length', 'Petal_Width']])     x['Petal_Cluster'] = kmeans_petal.labels_     # 打印前几行数据(including聚类结果)     print(x.head())     # print(y.Targets)         ###########################################################################################     # 计算轮廓系数         # 计算花萼聚类的轮廓系数     silhouette_sepal = silhouette_score(x[['Sepal_Length', 'Sepal_Width']], x['Sepal_Cluster'])     print("Silhouette Score for Sepal Clustering:", silhouette_sepal)     # 计算花瓣聚类的轮廓系数     silhouette_petal = silhouette_score(x[['Petal_Length', 'Petal_Width']], x['Petal_Cluster'])     print("Silhouette Score for Petal Clustering:", silhouette_petal)         ###########################################################################################     # 绘出聚类前后的图         # 绘制花萼的聚类前后对比图     plt.figure(figsize=(16, 7))     # 绘制花萼的原始数据散点图     plt.subplot(2, 2, 1)     plt.scatter(x['Sepal_Length'], x['Sepal_Width'], c=colormap[y['Targets']], s=40, label='Original Data')     plt.title('Original Sepal Data')     # 绘制花萼的聚类结果散点图     plt.subplot(2, 2, 2)     for cluster in np.unique(x['Sepal_Cluster']):         cluster_data = x[x['Sepal_Cluster'] == cluster]         plt.scatter(cluster_data['Sepal_Length'], cluster_data['Sepal_Width'], c=colormap[cluster], s=40, label=f'Cluster {cluster}')     plt.title('Sepal Clustering Overlay')     plt.legend()     # 绘制花瓣的聚类前后对比图     # 绘制花瓣的原始数据散点图     plt.subplot(2, 2, 3)     plt.scatter(x['Petal_Length'], x['Petal_Width'], c=colormap[y['Targets']], s=40, label='Original Data')     plt.title('Original Petal Data')     # 绘制花瓣的聚类结果散点图     plt.subplot(2, 2, 4)     for cluster in np.unique(x['Petal_Cluster']):         cluster_data = x[x['Petal_Cluster'] == cluster]         plt.scatter(cluster_data['Petal_Length'], cluster_data['Petal_Width'], c=colormap[cluster], s=40, label=f'Cluster {cluster}')     plt.title('Petal Clustering Overlay')     plt.legend()     plt.tight_layout()     plt.show()         ###########################################################################################     # 计算并输出Accuracy         # acc for sepal     accuracy_sepal = accuracy_score(iris.target, kmeans_sepal.labels_)     print("Accuracy for Sepal Clustering: {:.2f}%".format(accuracy_sepal * 100))         # acc for petal     accuracy_petal = accuracy_score(iris.target, kmeans_petal.labels_)     print("Accuracy for Petal Clustering: {:.2f}%".format(accuracy_petal * 100))         ###########################################################################################     # 计算并输出ARI(adjusted_rand_score)     """         ARI（Adjusted Rand Index）：         用于评估聚类结果与真实标签之间的一致性。取值范围在[-1, 1]之间，越接近1表示聚类效果越好。     """         # ARI for sepal     ari_score_sepal = adjusted_rand_score(iris.target, x['Sepal_Cluster'])     print("ARI for Sepal Clustering:", ari_score_sepal)         # ARI for petal     ari_score_petal = adjusted_rand_score(iris.target, x['Petal_Cluster'])     print("ARI for Petal Clustering:", ari_score_petal)

（2）数据集文本文件

"Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species" "1" 5.1 3.5 1.4 0.2 "setosa" "2" 4.9 3 1.4 0.2 "setosa" "3" 4.7 3.2 1.3 0.2 "setosa" "4" 4.6 3.1 1.5 0.2 "setosa" "5" 5 3.6 1.4 0.2 "setosa" "6" 5.4 3.9 1.7 0.4 "setosa" "7" 4.6 3.4 1.4 0.3 "setosa" "8" 5 3.4 1.5 0.2 "setosa" "9" 4.4 2.9 1.4 0.2 "setosa" "10" 4.9 3.1 1.5 0.1 "setosa" "11" 5.4 3.7 1.5 0.2 "setosa" "12" 4.8 3.4 1.6 0.2 "setosa" "13" 4.8 3 1.4 0.1 "setosa" "14" 4.3 3 1.1 0.1 "setosa" "15" 5.8 4 1.2 0.2 "setosa" "16" 5.7 4.4 1.5 0.4 "setosa" "17" 5.4 3.9 1.3 0.4 "setosa" "18" 5.1 3.5 1.4 0.3 "setosa" "19" 5.7 3.8 1.7 0.3 "setosa" "20" 5.1 3.8 1.5 0.3 "setosa" "21" 5.4 3.4 1.7 0.2 "setosa" "22" 5.1 3.7 1.5 0.4 "setosa" "23" 4.6 3.6 1 0.2 "setosa" "24" 5.1 3.3 1.7 0.5 "setosa" "25" 4.8 3.4 1.9 0.2 "setosa" "26" 5 3 1.6 0.2 "setosa" "27" 5 3.4 1.6 0.4 "setosa" "28" 5.2 3.5 1.5 0.2 "setosa" "29" 5.2 3.4 1.4 0.2 "setosa" "30" 4.7 3.2 1.6 0.2 "setosa" "31" 4.8 3.1 1.6 0.2 "setosa" "32" 5.4 3.4 1.5 0.4 "setosa" "33" 5.2 4.1 1.5 0.1 "setosa" "34" 5.5 4.2 1.4 0.2 "setosa" "35" 4.9 3.1 1.5 0.2 "setosa" "36" 5 3.2 1.2 0.2 "setosa" "37" 5.5 3.5 1.3 0.2 "setosa" "38" 4.9 3.6 1.4 0.1 "setosa" "39" 4.4 3 1.3 0.2 "setosa" "40" 5.1 3.4 1.5 0.2 "setosa" "41" 5 3.5 1.3 0.3 "setosa" "42" 4.5 2.3 1.3 0.3 "setosa" "43" 4.4 3.2 1.3 0.2 "setosa" "44" 5 3.5 1.6 0.6 "setosa" "45" 5.1 3.8 1.9 0.4 "setosa" "46" 4.8 3 1.4 0.3 "setosa" "47" 5.1 3.8 1.6 0.2 "setosa" "48" 4.6 3.2 1.4 0.2 "setosa" "49" 5.3 3.7 1.5 0.2 "setosa" "50" 5 3.3 1.4 0.2 "setosa" "51" 7 3.2 4.7 1.4 "versicolor" "52" 6.4 3.2 4.5 1.5 "versicolor" "53" 6.9 3.1 4.9 1.5 "versicolor" "54" 5.5 2.3 4 1.3 "versicolor" "55" 6.5 2.8 4.6 1.5 "versicolor" "56" 5.7 2.8 4.5 1.3 "versicolor" "57" 6.3 3.3 4.7 1.6 "versicolor" "58" 4.9 2.4 3.3 1 "versicolor" "59" 6.6 2.9 4.6 1.3 "versicolor" "60" 5.2 2.7 3.9 1.4 "versicolor" "61" 5 2 3.5 1 "versicolor" "62" 5.9 3 4.2 1.5 "versicolor" "63" 6 2.2 4 1 "versicolor" "64" 6.1 2.9 4.7 1.4 "versicolor" "65" 5.6 2.9 3.6 1.3 "versicolor" "66" 6.7 3.1 4.4 1.4 "versicolor" "67" 5.6 3 4.5 1.5 "versicolor" "68" 5.8 2.7 4.1 1 "versicolor" "69" 6.2 2.2 4.5 1.5 "versicolor" "70" 5.6 2.5 3.9 1.1 "versicolor" "71" 5.9 3.2 4.8 1.8 "versicolor" "72" 6.1 2.8 4 1.3 "versicolor" "73" 6.3 2.5 4.9 1.5 "versicolor" "74" 6.1 2.8 4.7 1.2 "versicolor" "75" 6.4 2.9 4.3 1.3 "versicolor" "76" 6.6 3 4.4 1.4 "versicolor" "77" 6.8 2.8 4.8 1.4 "versicolor" "78" 6.7 3 5 1.7 "versicolor" "79" 6 2.9 4.5 1.5 "versicolor" "80" 5.7 2.6 3.5 1 "versicolor" "81" 5.5 2.4 3.8 1.1 "versicolor" "82" 5.5 2.4 3.7 1 "versicolor" "83" 5.8 2.7 3.9 1.2 "versicolor" "84" 6 2.7 5.1 1.6 "versicolor" "85" 5.4 3 4.5 1.5 "versicolor" "86" 6 3.4 4.5 1.6 "versicolor" "87" 6.7 3.1 4.7 1.5 "versicolor" "88" 6.3 2.3 4.4 1.3 "versicolor" "89" 5.6 3 4.1 1.3 "versicolor" "90" 5.5 2.5 4 1.3 "versicolor" "91" 5.5 2.6 4.4 1.2 "versicolor" "92" 6.1 3 4.6 1.4 "versicolor" "93" 5.8 2.6 4 1.2 "versicolor" "94" 5 2.3 3.3 1 "versicolor" "95" 5.6 2.7 4.2 1.3 "versicolor" "96" 5.7 3 4.2 1.2 "versicolor" "97" 5.7 2.9 4.2 1.3 "versicolor" "98" 6.2 2.9 4.3 1.3 "versicolor" "99" 5.1 2.5 3 1.1 "versicolor" "100" 5.7 2.8 4.1 1.3 "versicolor" "101" 6.3 3.3 6 2.5 "virginica" "102" 5.8 2.7 5.1 1.9 "virginica" "103" 7.1 3 5.9 2.1 "virginica" "104" 6.3 2.9 5.6 1.8 "virginica" "105" 6.5 3 5.8 2.2 "virginica" "106" 7.6 3 6.6 2.1 "virginica" "107" 4.9 2.5 4.5 1.7 "virginica" "108" 7.3 2.9 6.3 1.8 "virginica" "109" 6.7 2.5 5.8 1.8 "virginica" "110" 7.2 3.6 6.1 2.5 "virginica" "111" 6.5 3.2 5.1 2 "virginica" "112" 6.4 2.7 5.3 1.9 "virginica" "113" 6.8 3 5.5 2.1 "virginica" "114" 5.7 2.5 5 2 "virginica" "115" 5.8 2.8 5.1 2.4 "virginica" "116" 6.4 3.2 5.3 2.3 "virginica" "117" 6.5 3 5.5 1.8 "virginica" "118" 7.7 3.8 6.7 2.2 "virginica" "119" 7.7 2.6 6.9 2.3 "virginica" "120" 6 2.2 5 1.5 "virginica" "121" 6.9 3.2 5.7 2.3 "virginica" "122" 5.6 2.8 4.9 2 "virginica" "123" 7.7 2.8 6.7 2 "virginica" "124" 6.3 2.7 4.9 1.8 "virginica" "125" 6.7 3.3 5.7 2.1 "virginica" "126" 7.2 3.2 6 1.8 "virginica" "127" 6.2 2.8 4.8 1.8 "virginica" "128" 6.1 3 4.9 1.8 "virginica" "129" 6.4 2.8 5.6 2.1 "virginica" "130" 7.2 3 5.8 1.6 "virginica" "131" 7.4 2.8 6.1 1.9 "virginica" "132" 7.9 3.8 6.4 2 "virginica" "133" 6.4 2.8 5.6 2.2 "virginica" "134" 6.3 2.8 5.1 1.5 "virginica" "135" 6.1 2.6 5.6 1.4 "virginica" "136" 7.7 3 6.1 2.3 "virginica" "137" 6.3 3.4 5.6 2.4 "virginica" "138" 6.4 3.1 5.5 1.8 "virginica" "139" 6 3 4.8 1.8 "virginica" "140" 6.9 3.1 5.4 2.1 "virginica" "141" 6.7 3.1 5.6 2.4 "virginica" "142" 6.9 3.1 5.1 2.3 "virginica" "143" 5.8 2.7 5.1 1.9 "virginica" "144" 6.8 3.2 5.9 2.3 "virginica" "145" 6.7 3.3 5.7 2.5 "virginica" "146" 6.7 3 5.2 2.3 "virginica" "147" 6.3 2.5 5 1.9 "virginica" "148" 6.5 3 5.2 2 "virginica" "149" 6.2 3.4 5.4 2.3 "virginica" "150" 5.9 3 5.1 1.8 "virginica"