C++递归算法理解及典型问题举例
C++递归算法理解
- 递归与循环的关系
- 递归的内涵
- 递归与循环
- 经典递归问题实战
本文剖析了递归的思想内涵,分析了递归与循环的联系与区别,给出了递归的应用场景和一些典型应用,并利用递归和非递归的方式解决了包括阶乘、斐波那契数列、汉诺塔、杨辉三角的存取、字符串回文判断、字符串全排列、二分查找、树的深度求解在内的八个经典问题。
递归与循环的关系
比喻
递归:你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,你继续打开它。若干次之后,你打开面前的门后,发现只有一间屋子,没有门了。然后,你开始原路返回,每走回一间屋子,你数一次,走到入口的时候,你可以回答出你到底用这你把钥匙打开了几扇门。
循环:你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门(若前面两扇门都一样,那么这扇门和前两扇门也一样;如果第二扇门比第一扇门小,那么这扇门也比第二扇门小,你继续打开这扇门,一直这样继续下去直到打开所有的门。但是,入口处的人始终等不到你回去告诉他答案。
递归的内涵
1、定义
在数学与计算机科学中,递归(Recursion)是指在函数的定义中使用函数自身的方法。实际上,递归,顾名思义,其包含了两个意思:递和归,这正是递归思想的精华所在。
2、递归思想的内涵(递归的精髓是什么?)
递归就是有去(递去)有回(归来),如下图所示。“有去”是指:递归问题必须可以分解为若干个规模较小,与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决,就像上面例子中的钥匙可以打开后面所有门上的锁一样;“有回”是指 : 这些问题的演化过程是一个从大到小,由近及远的过程,并且会有一个明确的终点(临界点),一旦到达了这个临界点,就不用再往更小、更远的地方走下去。最后,从这个临界点开始,原路返回到原点,原问题解决。
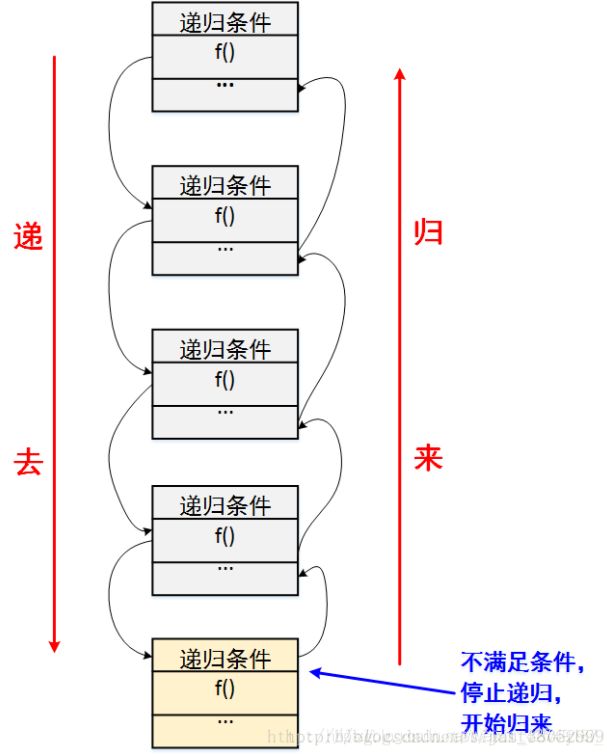
递归的基本思想就是把规模大的问题转化为规模小的相似的子问题来解决。特别地,在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况,这也正是递归的定义所在。格外重要的是,这个解决问题的函数必须有明确的结束条件,否则就会导致无限递归的情况。
3、递归的三要素
在我们了解了递归的基本思想及其数学模型之后,我们如何才能写出一个漂亮的递归程序呢?主要是把握好如下三个方面:
1、明确递归终止条件;
递归就是有去有回,必然应该有一个明确的临界点,程序一旦到达了这个临界点,就不用继续往下递去而是开始实实在在的归来。换句话说,该临界点就是一种简单情境,可以防止无限递归。
2、给出递归终止时的处理办法;
递归的临界点存在一种简单情境,在这种简单情境下,我们应该直接给出问题的解决方案。一般地,在这种情境下,问题的解决方案是直观的、容易的。
3、提取重复的逻辑,缩小问题规模。
递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决。从程序实现的角度而言,我们需要抽象出一个干净利落的重复的逻辑,以便使用相同的方式解决子问题。
4、递归算法的编程模型 明确递归算法设计三要素后,接下来就需要着手开始编写具体的算法了。这里给出两种典型的递归算法设计模型,如下所示:
模型一: 在递去的过程中解决问题
function recursion(大规模){
if (end_condition){ // 明确的递归终止条件
end; // 简单情景
}else{ // 在将问题转换为子问题的每一步,解决该步中剩余部分的问题
solve; // 递去
recursion(小规模); // 递到最深处后,不断地归来
}
}
模型二: 在归来的过程中解决问题
function recursion(大规模){
if (end_condition){ // 明确的递归终止条件
end; // 简单情景
}else{ // 先将问题全部描述展开,再由尽头“返回”依次解决每步中剩余部分的问题
recursion(小规模); // 递去
solve; // 归来
}
}
5、递归的应用场景
递归算法一般用于解决三类问题:
(1). 问题的定义是按递归定义的(Fibonacci函数,阶乘,…);
(2). 问题的解法是递归的(有些问题只能使用递归方法来解决,例如,汉诺塔问题,…);
(3). 数据结构是递归的(链表、树等的操作,包括树的遍历,树的深度,…)。
在下文我们将给出递归算法的一些经典应用案例,这些案例基本都属于这三种类型问题的范畴。
递归与循环
递归与循环是两种不同的解决问题的典型思路。递归通常很直白地描述了一个问题的求解过程,因此也是最容易被想到解决方式。循环其实和递归具有相同的特性,即做重复任务,但有时使用循环的算法并不会那么清晰地描述解决问题步骤。单从算法设计上看,递归和循环并无优劣之别。然而,在实际开发中,因为函数调用的开销,递归常常会带来性能问题,特别是在求解规模不确定的情况下;而循环因为没有函数调用开销,所以效率会比递归高。递归求解方式和循环求解方式往往可以互换,也就是说,如果用到递归的地方可以很方便使用循环替换,而不影响程序的阅读,那么替换成循环往往是好的。问题的递归实现转换成非递归实现一般需要两步工作:
(1). 自己建立“堆栈(一些局部变量)”来保存这些内容以便代替系统栈,比如树的三种非递归遍历方式;
(2). 把对递归的调用转变为对循环处理。
特别地,在下文中我们将给出递归算法的一些经典应用案例,对于这些案例的实现,我们一般会给出递归和非递归两种解决方案,以便读者体会。
经典递归问题实战
第一类问题:问题的定义是按递归定义的
(1). 阶乘
class Factorial {
public:
/**
* @description 阶乘的递归实现
* @param n
* @return
*/
static long f(int n) {
if (n == 1) { // 递归终止条件
return 1; // 简单情景
}
return n*f(n - 1); // 相同重复逻辑,缩小问题的规模
}
//--------------------------------我是分割线-------------------------------------
/**
* @description 阶乘的非递归实现
* @param n
* @return
*/
static long f_loop(int n) {
long result = n;
while (n > 1) {
n--;
result = result * n;
}
return result;
}
};
(2). 斐波纳契数列
- Title: 斐波纳契数列
- Description: 斐波纳契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……
- 在数学上,斐波纳契数列以如下被以递归的方法定义:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*)。
- 两种递归解法:经典解法和优化解法
- 两种非递归解法:递推法和数组法
class FibonacciSequence {
public:
/**
* @description 经典递归法求解
* 斐波那契数列如下:
* 1,1,2,3,5,8,13,21,34,...
* *那么,计算fib(5)时,需要计算1次fib(4),2次fib(3),3次fib(2),调用了2次fib(1)*,即:
* fib(5) = fib(4) + fib(3)
* fib(4) = fib(3) + fib(2) ;fib(3) = fib(2) + fib(1)
* fib(3) = fib(2) + fib(1)
* 这里面包含了许多重复计算,而实际上我们只需计算fib(4)、fib(3)、fib(2)和fib(1)各一次即可,
* 后面的optimizeFibonacci函数进行了优化,使时间复杂度降到了O(n).
* @param n 目标项
* @return
*/
static int fibonacci(int n) {
if (n == 1 || n == 2) { // 递归终止条件
return 1; // 简单情景
}
return fibonacci(n - 1) + fibonacci(n - 2); // 相同重复逻辑,缩小问题的规模
}
//--------------------------------我是分割线-------------------------------------
/**
* @description 对经典递归法的优化
* 斐波那契数列如下:
* 1,1,2,3,5,8,13,21,34,...
* 那么,我们可以这样看:fib(1,1,5) = fib(1,2,4) = fib(2,3,3) = 5
* 也就是说,以1,1开头的斐波那契数列的第五项正是以1,2开头的斐波那契数列的第四项,
* 而以1,2开头的斐波那契数列的第四项也正是以2,3开头的斐波那契数列的第三项,
* 更直接地,我们就可以一步到位:fib(2,3,3) = 2 + 3 = 5,计算结束。
* 注意,前两个参数是数列的开头两项,第三个参数是我们想求的以前两个参数开头的数列的第几项。
* 时间复杂度:O(n)
* @param first 数列的第一项
* @param second 数列的第二项
* @param n 目标项
* @return
*/
static int optimizeFibonacci(int first, int second, int n) {
if (n > 0) {
if (n == 1) { // 递归终止条件
return first; // 简单情景
}
else if (n == 2) { // 递归终止条件
return second; // 简单情景
}
else if (n == 3) { // 递归终止条件
return first + second; // 简单情景
}
return optimizeFibonacci(second, first + second, n - 1); // 相同重复逻辑,缩小问题规模
}
return -1;
}
//--------------------------------我是分割线-------------------------------------
/**
* @description 非递归解法:有去无回
* @param n
* @return
*/
static int fibonacci_loop(int n) {
if (n == 1 || n == 2) {
return 1;
}
int result = -1;
int first = 1, second = 1; // 自己维护的"栈",以便状态回溯
for (int i = 3; i <= n; i++) { // 循环
result = first + second;
first = second;
second = result;
}
return result;
}
//--------------------------------我是分割线-------------------------------------
/**
* @description 使用数组存储斐波那契数列
* @param n
* @return
*/
static int fibonacci_array(int n) {
if (n > 0) {
int arr[100]; // 使用临时数组存储斐波纳契数列
arr[0] = arr[1] = 1;
for (int i = 2; i < n; i++) { // 为临时数组赋值
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n - 1];
}
return -1;
}
};
(3). 杨辉三角的取值
/**
* Title: 杨辉三角形又称Pascal三角形,它的第i+1行是(a+b)i的展开式的系数。
* 它的一个重要性质是:三角形中的每个数字等于它两肩上的数字相加。
* 例如,下面给出了杨辉三角形的前4行:
* 1
* 1 1
* 1 2 1
* 1 3 3 1
* @description 递归获取杨辉三角指定行、列(从0开始)的值
* 注意:与是否创建杨辉三角无关
*/
class Pascal {
public:
/**
* @description 递归获取杨辉三角指定行、列(从0开始)的值
* 注意:与是否创建杨辉三角无关
* @x 指定行
* @y 指定列
*/
static int getValue(int x, int y) {
if (y <= x && y >= 0) {
if (y == 0 || x == y) { // 递归终止条件
return 1;
}
else {
// 递归调用,缩小问题的规模
return getValue(x - 1, y - 1) + getValue(x - 1, y);
}
}
return -1;
}
};
(3). 回文字符串的判断
/**
* Title: 回文字符串的判断
* Description: 回文字符串就是正读倒读都一样的字符串。如”98789”, “abccba”都是回文字符串
* 两种解法:
* 递归判断;
* 循环判断;
*/
class PalindromeString {
/**
* @description 递归判断一个字符串是否是回文字符串
* @param s
* @return
*/
public:
static bool isPalindromeString_recursive(string s) {
int start = 0;
int end = s.length()-1;
if (end > start) { // 递归终止条件:两个指针相向移动,当start超过end时,完成判断
if (s[start] != s[end]) {
return false;
}
else {
// 递归调用,缩小问题的规模
return isPalindromeString_recursive(s.substr(start+1, end-1));
//return isPalindromeString_recursive(s.substring(start + 1).substring(0, end - 1));
}
}
return true;
}
//--------------------------------我是分割线-------------------------------------
/**
* @description 循环判断回文字符串
* @param s
* @return
*/
static bool isPalindromeString_loop(string s) {
int start = 0;
int end = s.length() - 1;
while (end > start) { // 循环终止条件:两个指针相向移动,当start超过end时,完成判断
if (s[end] != s[start]) {
return false;
}
else {
end--;
start++;
}
}
return true;
}
};
(5). 字符串全排列
class Permutation {
public:
/**
* 递归解法
* @description 从字符串数组中每次选取一个元素,作为结果中的第一个元素;然后,对剩余的元素全排列
* @param s 字符数组
* @param from 起始下标
* @param to 终止下标
*/
static void getStringPermutations3(vector<char> &s, int from, int to) {
if (s.empty() || to < from || to >= s.size() || from < 0) { // 边界条件检查
return;
}
if (from == to) { // 递归终止条件
for (int i = 0; i <= to; i++) { // 打印结果
cout << s[i] << " ";
}
cout << endl;
}
else {
for (int i = from; i <= to; i++) {
swap(s, i, from); // 交换前缀,作为结果中的第一个元素,然后对剩余的元素全排列
getStringPermutations3(s, from + 1, to); // 递归调用,缩小问题的规模
swap(s, from, i); // 换回前缀,复原字符数组
}
}
}
/**
* @description 对字符数组中的制定字符进行交换
* @param s 字符数组
* @param from 起始下标
* @param to 终止下标
*/
static void swap(vector<char> &s, int from, int to) {
char temp = s[from];
s[from] = s[to];
s[to] = temp;
}
};
/**
* 非递归解法(字典序全排列)
* Title: 字符串全排列非递归算法(字典序全排列)
* Description: 字典序全排列,其基本思想是:
* 先对需要求排列的字符串进行字典排序,即得到全排列中最小的排列.
* 然后,找到一个比它大的最小的全排列,一直重复这一步直到找到最大值,即字典排序的逆序列.
* 不需要关心字符串长度
*/
class StringPermutationsLoop {
public:
/**
* @description 获取序列的极值
* @param s 序列
* @param from 起始下标
* @param to 终止下标
* @return
*/
static int getExtremum(vector<char> &s, int from, int to) {
int index = 0;
for (int i = to; i > from; i--) {
if (s[i] > s[i - 1]) {
index = i;
break;
}
}
return index;
}
/**
* @description 从top处查找比s[top-1]大的最小值所在的位置
* @param s
* @param top 极大值所在位置
* @param to
* @return
*/
static int getMinMax(vector<char> &s, int top, int to) {
int index = top;
char base = s[top - 1];
char temp = s[top];
for (int i = top + 1; i <= to; i++) {
if (s[i] > base && s[i] < temp) {
temp = s[i];
index = i;
}
continue;
}
return index;
}
/**
* @description 对字符数组中的制定字符进行交换
* @param s 字符数组
* @param from 起始下标
* @param to 终止下标
*/
static void swap(vector<char> &s, int from, int to) {
char temp = s[from];
s[from] = s[to];
s[to] = temp;
}
/**
* @description 翻转top(包括top)后的序列
* @param s
* @param from
* @param to
* @return
*/
static vector<char> reverse(vector<char> &s, int top, int to) {
char temp;
while (top < to) {
temp = s[top];
s[top++] = s[to];
s[to--] = temp;
}
return s;
}
/**
* @description 字典序全排列
* 设一个字符串(字符数组)的全排列有n个,分别是A1,A2,A3,...,An
* 1. 找到最小的排列 Ai
* 2. 找到一个比Ai大的最小的后继排列Ai+1
* 3. 重复上一步直到没有这样的后继
* 重点就是如何找到一个排列的直接后继:
* 对于字符串(字符数组)a0a1a2……an,
* 1. 从an到a0寻找第一次出现的升序排列的两个字符(即ai < ai+1),那么ai+1是一个极值,因为ai+1之后的字符为降序排列,记 top=i+1;
* 2. 从top处(包括top)开始查找比ai大的最小的值aj,记 minMax = j;
* 3. 交换minMax处和top-1处的字符;
* 4. 翻转top之后的字符(包括top),即得到一个排列的直接后继排列
* @param s 字符数组
* @param from 起始下标
* @param to 终止下标
*/
static void getStringPermutations4(vector<char> &s, int from, int to) {
if (s.empty() || to < from || to >= s.size() || from < 0) { // 边界条件检查
return;
}
sort(s.begin(), s.end()); // 对字符数组的所有元素进行升序排列,即得到最小排列
for (char it : s) {
cout << it << " ";
}
cout << endl;
vector<char> descendArr(s);
sort(descendArr.rbegin(), descendArr.rend()); // 对字符数组的所有元素进行降序排列,即得到最大排列
while (s != descendArr) { // 循环终止条件:迭代至最大排列
int top = getExtremum(s, from, to); // 从尾部开始找到序列的极值
int minMax = getMinMax(s, top, to); // 从top处(包括top)查找比s[top-1]大的最小值所在的位置
swap(s, top - 1, minMax); // 交换minMax处和top-1处的字符
s = reverse(s, top, to); // 翻转top之后的字符
for (char it : s) {
cout << it << " ";
}
cout << endl;
}
}
};
链接: link.
(6). 二分查找
class BinarySearch {
public:
/** @description 二分查找的递归实现
* @param array 目标数组
* @param low 左边界
* @param high 右边界
* @param target 目标值
* @return 目标值所在位置
*/
static int binarySearch(int array[], int low, int high, int target) {
// 递归终止条件
if (low <= high) {
int mid = low + (high - low >> 1);
if (array[mid] == target) {
return mid + 1; // 返回目标值的位置,从1开始
}
else if (array[mid] > target) {
return binarySearch(array, low, mid - 1, target); // 由于array[mid]不是目标值,因此再次递归搜索时,可以将其排除
}
else {
return binarySearch(array, mid + 1, high, target); // 由于array[mid]不是目标值,因此再次递归搜索时,可以将其排除
}
}
return -1; //表示没有搜索到
}
//--------------------------------我是分割线-------------------------------------
/** @description 二分查找的非递归实现
* @param array 目标数组
* @param low 左边界
* @param high 右边界
* @param target 目标值
* @return 目标值所在位置
*/
static int binarySearchNoRecursive(int array[], int low, int high, int target) {
// 循环
while (low <= high) {
int mid = (low + high) >> 1;
if (array[mid] == target) {
return mid + 1; // 返回目标值的位置,从1开始
}
else if (array[mid] > target) {
high = mid - 1; // 由于array[mid]不是目标值,因此再次递归搜索时,可以将其排除
}
else {
low = mid + 1; // 由于array[mid]不是目标值,因此再次递归搜索时,可以将其排除
}
}
return -1; // 表示没有搜索到
}
};
第二类问题:问题解法按递归算法实现
(1). 汉诺塔问题
/**
* Title: 汉诺塔问题
* Description:古代有一个梵塔,塔内有三个座A、B、C,A座上有64个盘子,盘子大小不等,大的在下,小的在上。
* 有一个和尚想把这64个盘子从A座移到C座,但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘子始终保持大盘在下,
* 小盘在上。在移动过程中可以利用B座。要求输入层数,运算后输出每步是如何移动的。
*/
class HanoiTower {
public:
/**
* @description 在程序中,我们把最上面的盘子称为第一个盘子,把最下面的盘子称为第N个盘子
* @param level:盘子的个数
* @param from 盘子的初始地址
* @param inter 转移盘子时用于中转
* @param to 盘子的目的地址
*/
static void moveDish(int level, char from, char inter, char to) {
if (level == 1) { // 递归终止条件
cout << "从 " << from << " 移动盘子 " << level << " 号到" << to << endl;
}
else {
// 递归调用:将level-1个盘子从from移到inter(不是一次性移动,每次只能移动一个盘子,其中to用于周转)
moveDish(level - 1, from, to, inter); // 递归调用,缩小问题的规模,将第level个盘子从A座移到C座
cout << "从 " << from << " 移动盘子 " << level << " 号到" << to << endl;
// 递归调用:将level-1个盘子从inter移到to,from 用于周转
moveDish(level - 1, inter, from, to); // 递归调用,缩小问题的规模
}
}
};
第三类问题:数据的结构是按递归定义的
二叉树深度
/**
* Title: 递归求解二叉树的深度
* Description:
*/
class BinaryTreeDepth {
public:
/**
* @description 返回二叉数的深度
* @param t
* @return
*/
static int getTreeDepth(TreeNode *t) {
// 树为空
if (t == nullptr) { // 递归终止条件
return 0;
}
int left = getTreeDepth(t->left); // 递归求左子树深度,缩小问题的规模
int right = getTreeDepth(t->right); // 递归求右子树深度,缩小问题的规模
return left > right ? left + 1 : right + 1;
}
};
二叉树前序遍历
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {
}
};
class BinaryTreePreorderTraversal {
public:
/**
* @description 前序遍历(递归)
* @param root
* @return
*/
static void preOrder(TreeNode *root) {
if (root == nullptr) { // 递归终止条件
return;
}
else { // 递归
cout << root->val << endl; // 前序遍历当前结点
preOrder(root->left); // 前序遍历左子树
preOrder(root->right); // 前序遍历右子树
return;
}
}
};