机器学习基本概念2
资料来源:
https://www.youtube.com/watch?v=Ye018rCVvOo&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=1
https://www.youtube.com/watch?v=bHcJCp2Fyxs&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=2
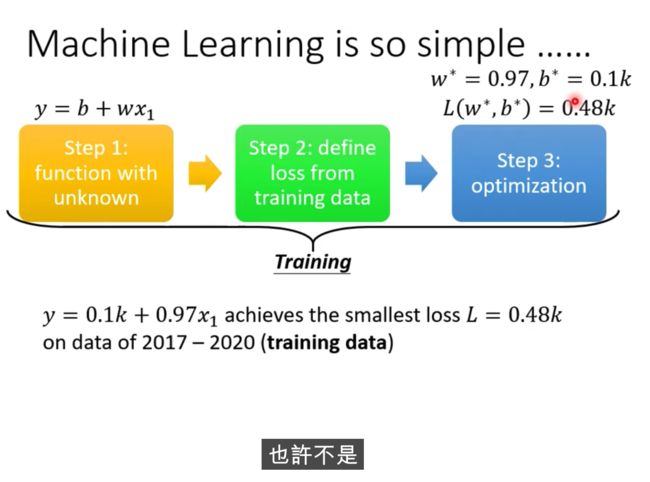
分三步
1、 定义function
b和w是需要透过知识去获取的,是未知的
做机器学习,需要Domain Knowledge,这些知识就是用来解b和w
这里的函式,就叫做Model
我们知道2月25号的人数是多少,就叫feauture
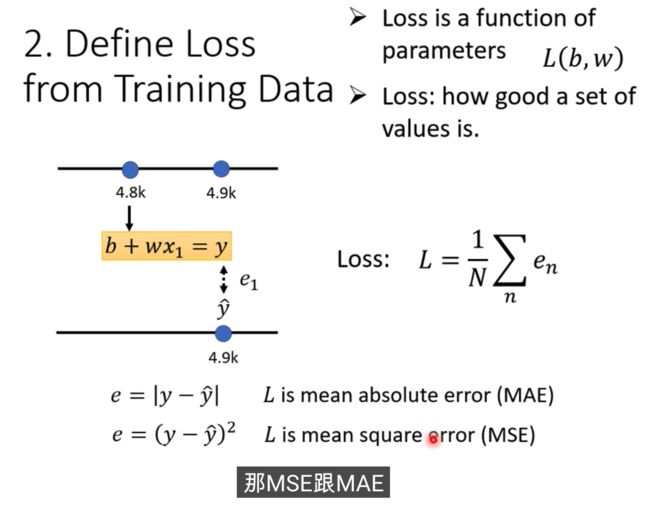
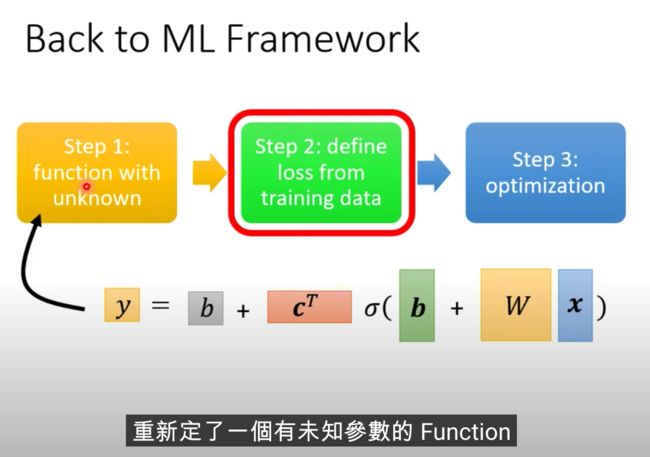
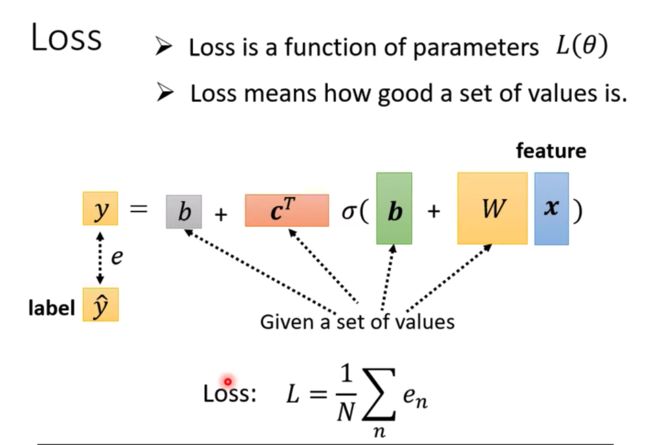
2、 定义Loss
Loss is a function of parameters
真实的值叫Label(正确的数值)
可以算出来最近3年的误差,把所有的误差加起来,算出来一个L,这就是我们的Loss,值越大,说明越不好
MAE和MSE的区别和选择具体而定,还有Cross-entropy
真实的后台统计数据例子
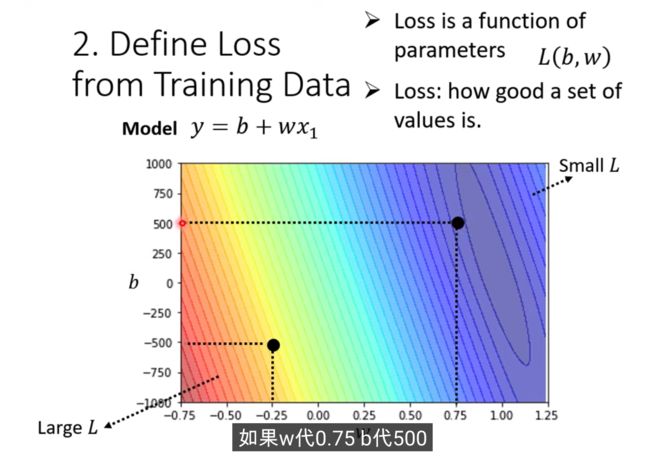
越偏红色,代表Loss越大,偏蓝色,Loss越小,那在预测的时候,w为0.75 b代500,可能预测会更准
3、最佳化算法
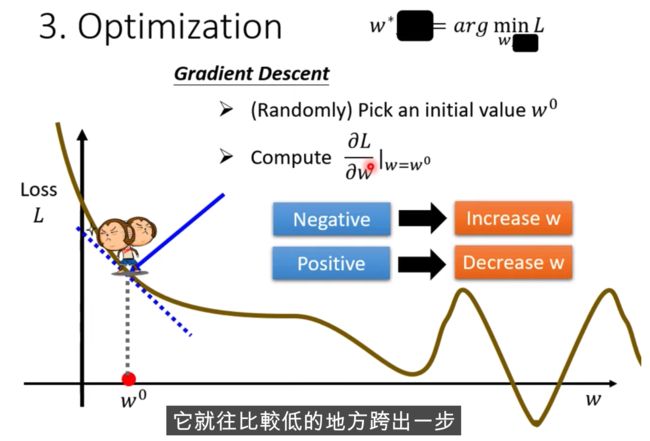
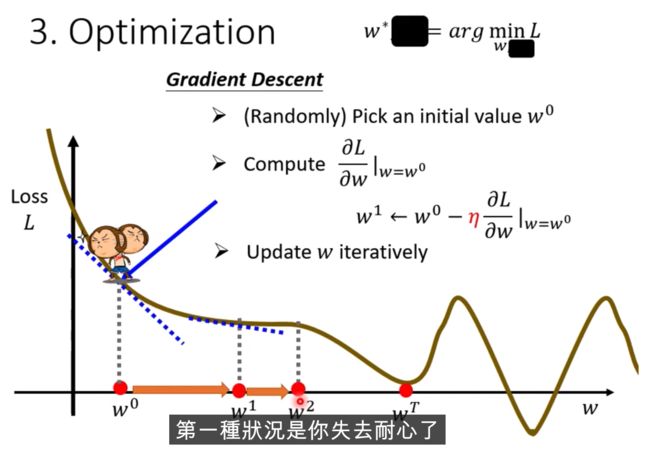
做法: Gradient Descent
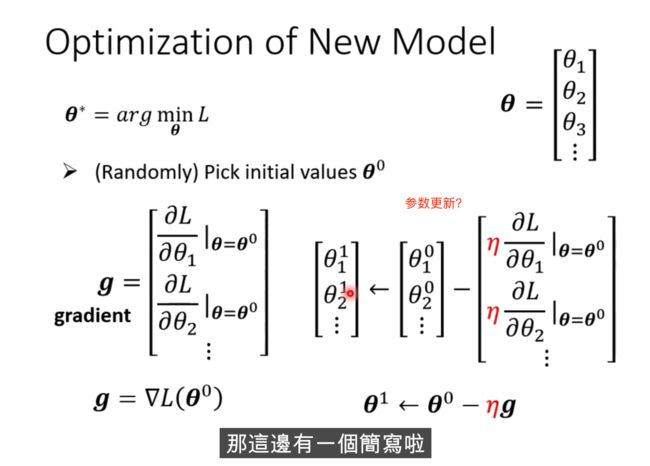
如何做: 当w不同的值时,会得到不同的Loss,
怎么找到w,让Loss最小,随机选取初始化的点 w0(有一些方法可以更科学的找到这个值)
计算w对l的微积分,计算error surface的斜率,如果这个斜率的值为负数,
把w的值变大,Loss就会小
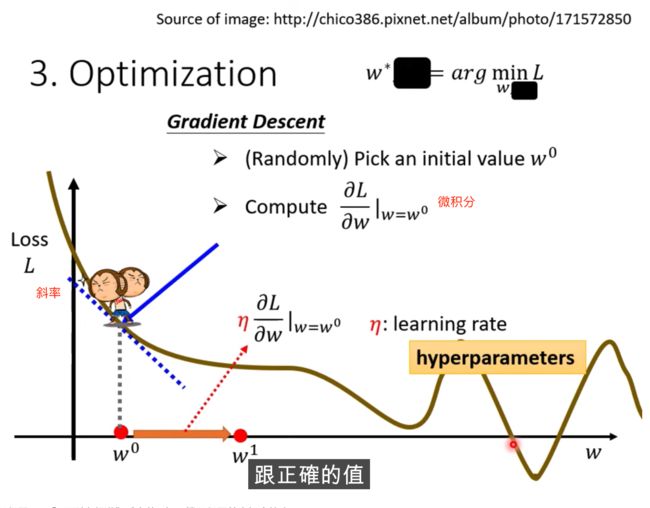
跨步要多大呢?
斜率大,就跨大
学习速率是自己设定的
Loss的值为什么会是负数?
因为这个函数是自己定义的,Loss的定义的估算的值和实际的值的绝对值,如果根据刚刚的定义,不可能为负数
但上面的这个例子不是真实的案例,error surface 可能是任何形状
hyperparameter,自己设定的
什么时候会停止下来?一般两种情况
a、 前期设定了这个参数,例如次数
b、 达到了理想的状态
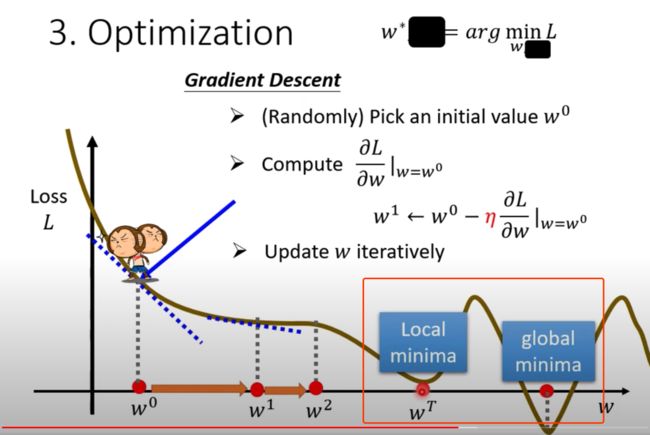
Gradient Descent上面找不到最佳的loss值,因为随机的位置不一样
Local minima是个假的问题,具体为什么,后面会讲
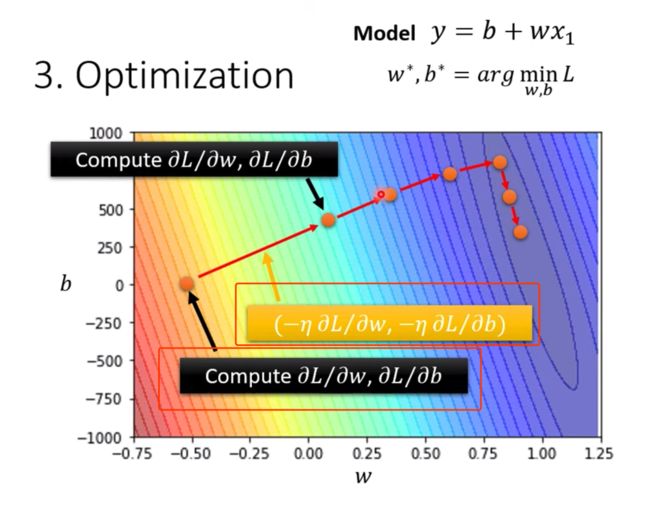
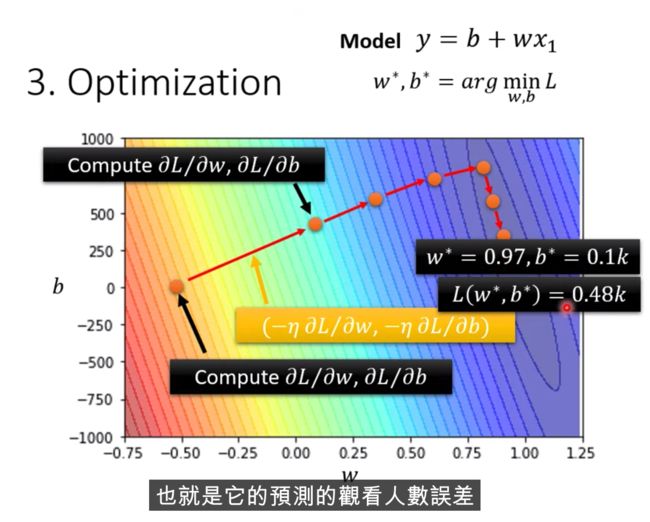
两个参数,如何做上面的Graddient Descent?
例子
课程总结:
这三个步骤合并起来,叫做训练
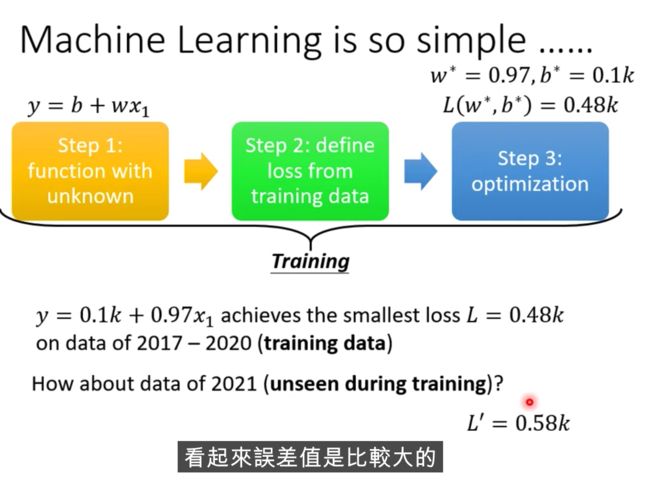
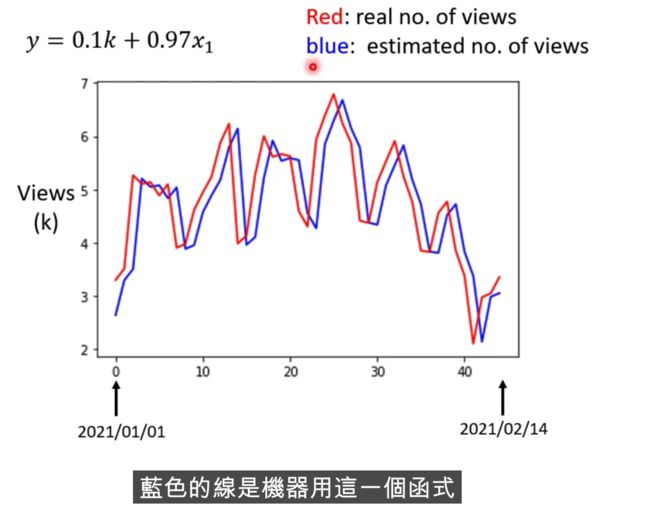
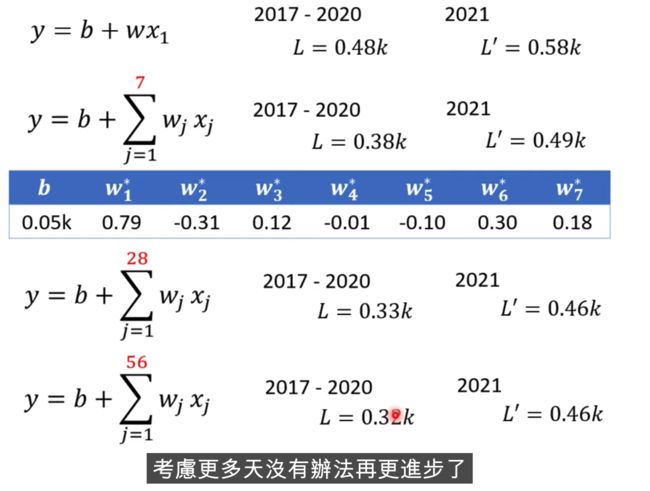
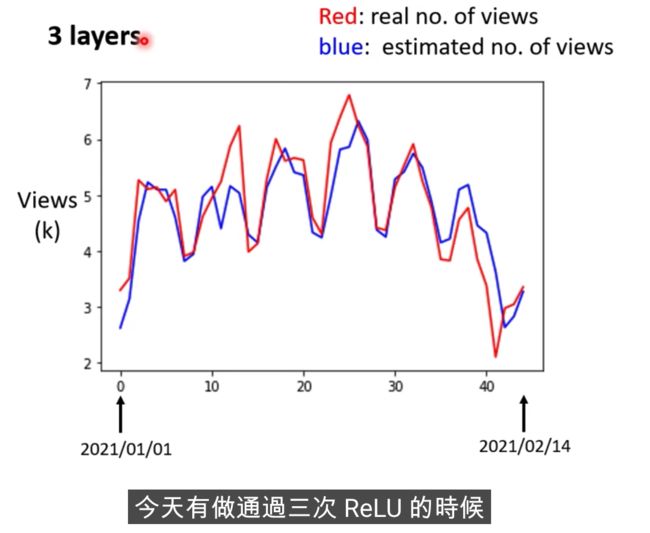
2021年的误差还是比较大的,怎么做的更好? 分析下数据
蓝色线相当于把红色右移了一天而已,每隔7天就是一个循环
这个model是一个比较坏的,我们可以拿7天的周期来进行修改
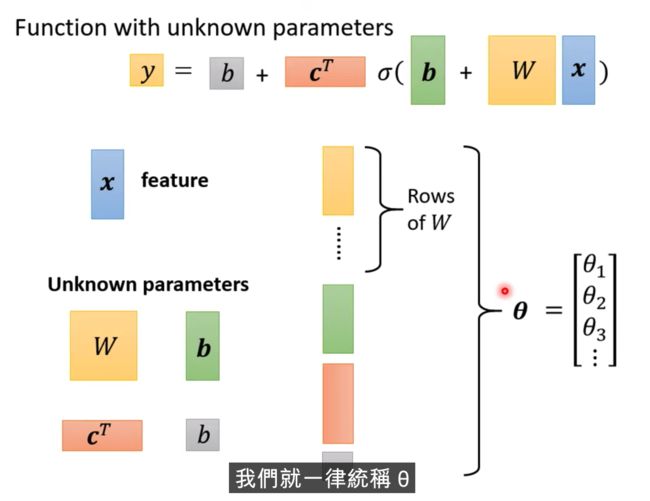
x叫做feature
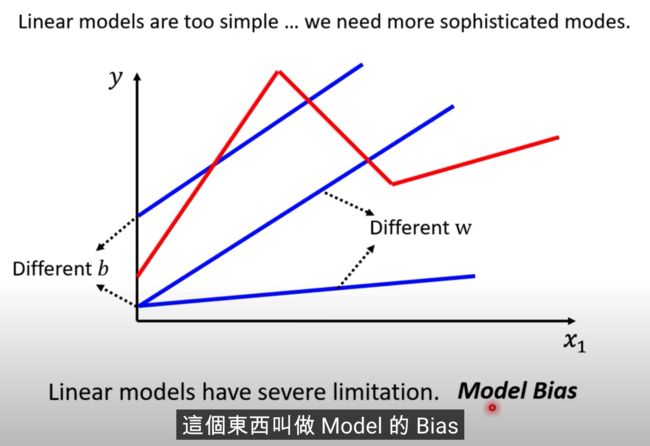
上面的叫做Linear Model,我们后面看下怎么把Linear Model做的更好
Linear Model 太过简单了
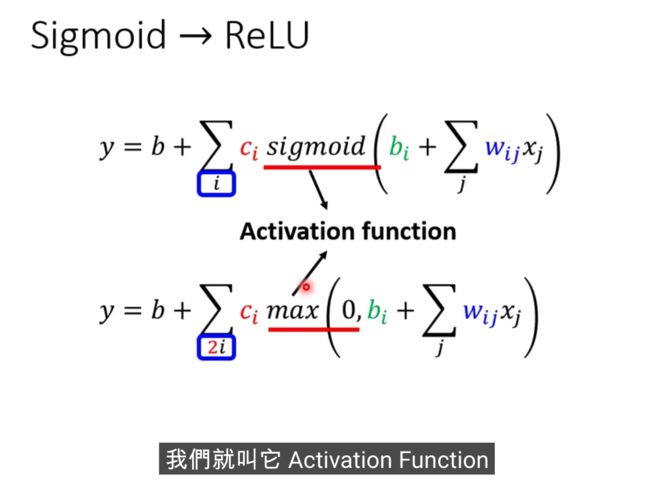
我们需要写出更复杂,更多未知参数的function
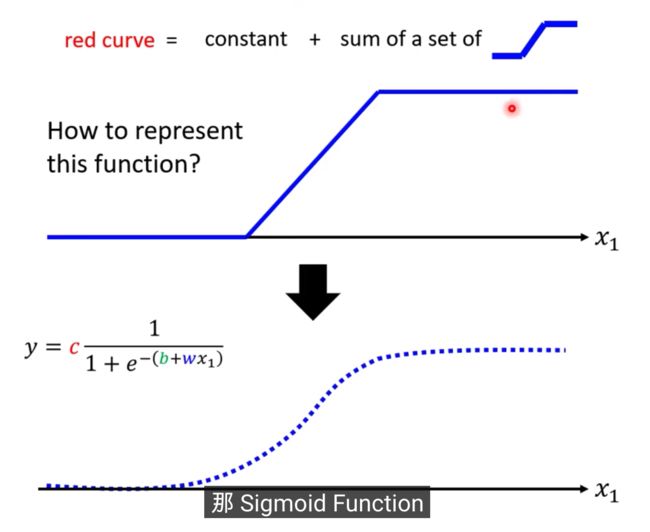
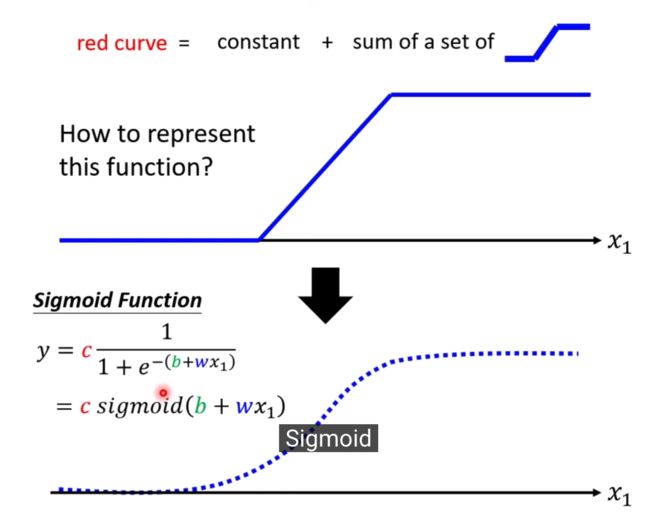
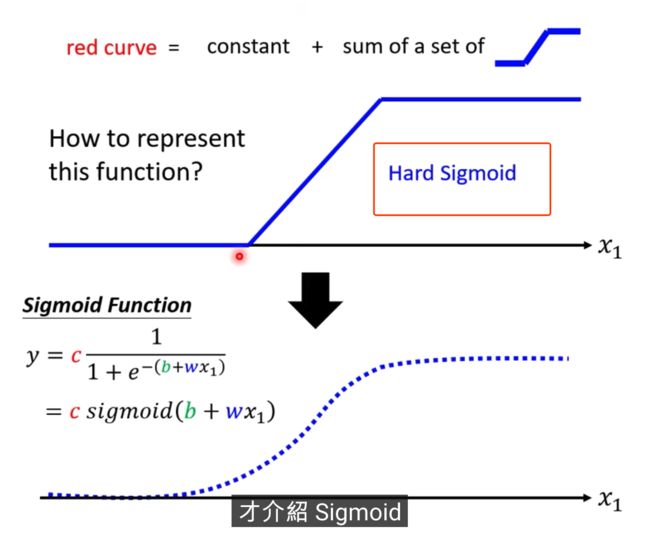
1除以1+Exponential-b+wx1,再乘以constant常数
当b+wx1趋向于无穷大的时候,会发生什么事呢,Exponential会消失,当X1非常大的时候,这一条线会收敛在高度是C的地方
当b+wx1趋向于负的无穷大,分母会非常大,Y的值会趋近于0
S型的function,叫做sigmoid
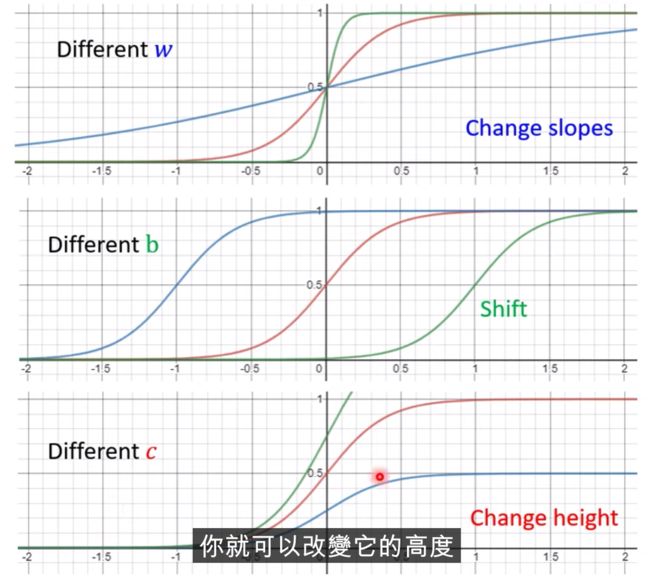
我们需要各式各样合适蓝色的function,那这个蓝色function怎么出来呢,需要调整b和w
改w,会改变斜率,斜坡的坡度
修改b呢,会左右移动
修改c,会改变高度
可以制造出不同
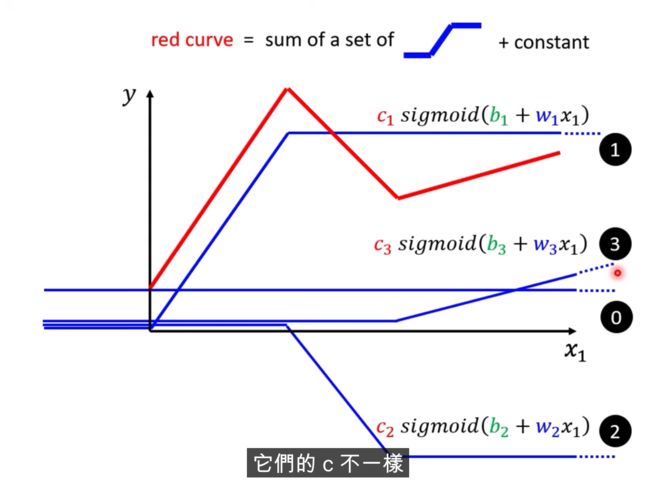
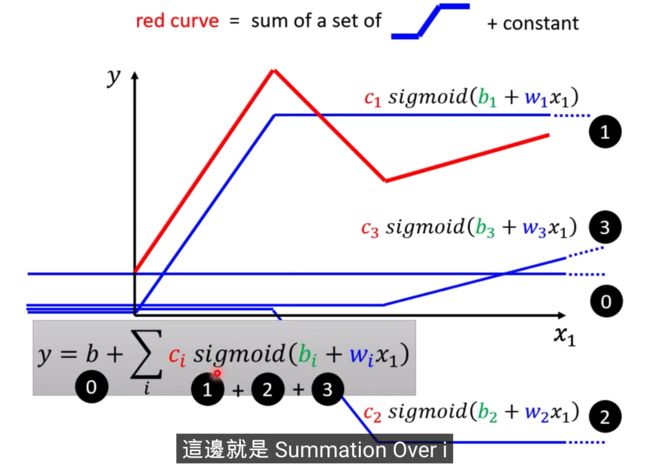
把0和1和2和3都加起来
summation,b是constant
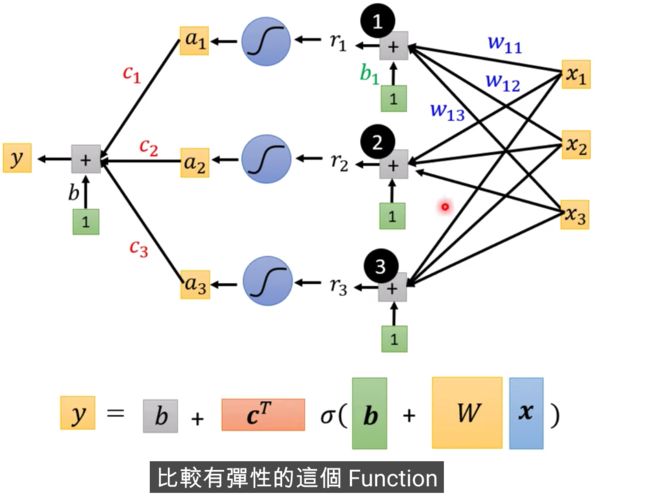
假设b,c,w是未知参数,有弹性,有未知参数的函式
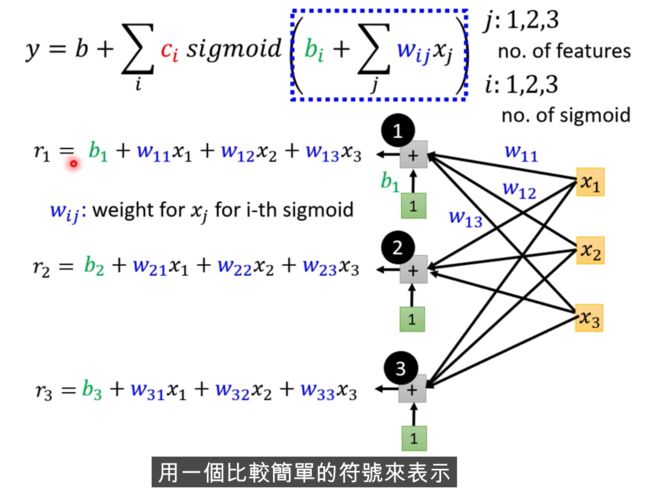
Transpose
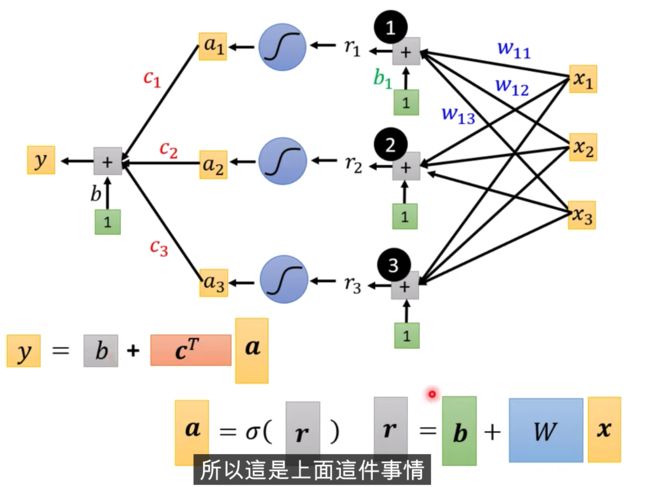
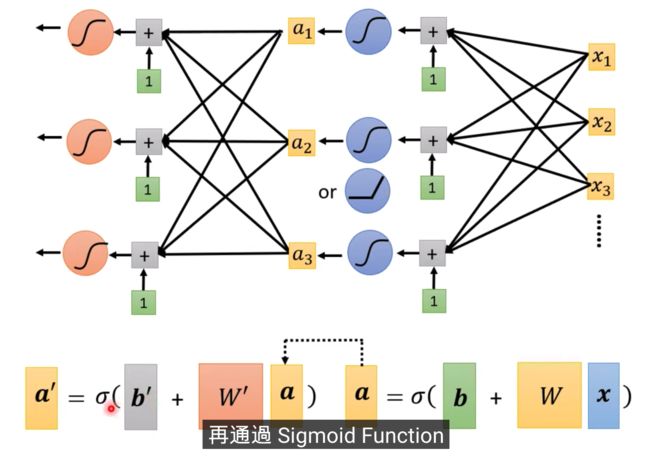
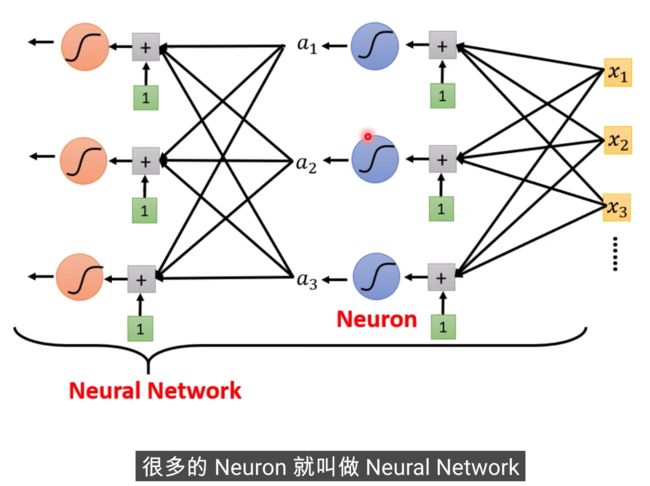
X输入,我们的Feature是X这个向量,X乘上矩阵W加上向量b,得到向量r,再把向量r,通过Sigmooid Function得到向量a,
再把向量a跟乘上c的Transpose加上b,就得到了y
不同的表示方式,上面是图示化的方式,下面是线性代数的表示方式
在参数小的情况下,穷举所有的可能就行,不需要使用Gradient Descent
Sigmoid 可以有多个,会产生越多线段的 Piecewise Linear的function,你就可以逼近越复杂的function
至于需要几个Sigmoid,这是另外的Hyper Parameter,这个自己决定
Loss function
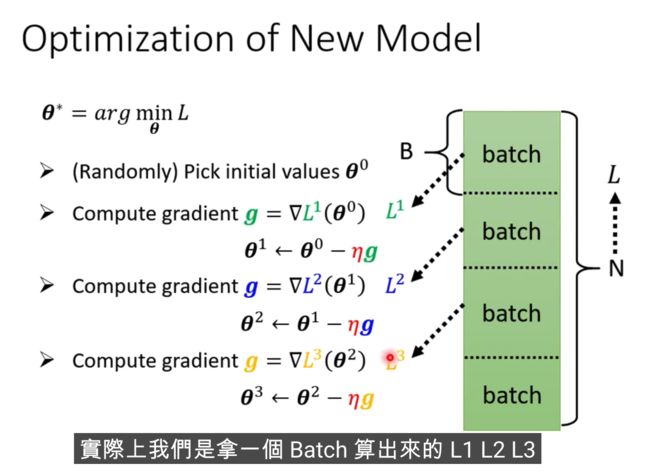
Update和Epoch是不一样的东西
每次更新一次参数叫做一次update,把所有的Batch都看过一遍,叫做一个Epoch
为什么要分成一个一个的batch?
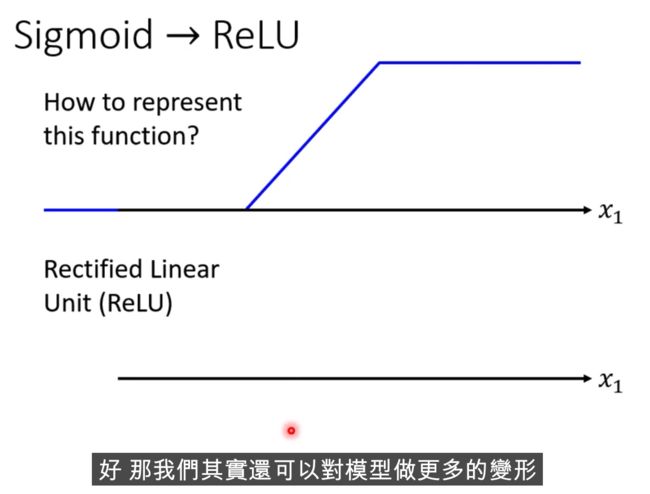
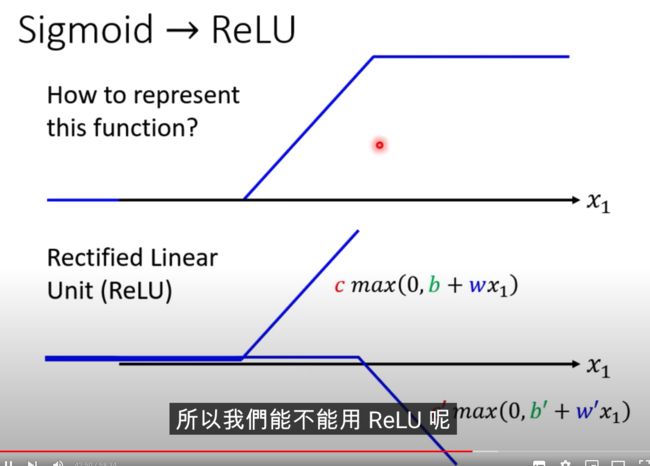
激活函数
哪种比较好?? Relu好一些
我们还可以继续改我们的模型
我们可以把重复的事情,反复的再多做几次,这里的几次,又是另外一个超参数
模型也需要一个好的名字
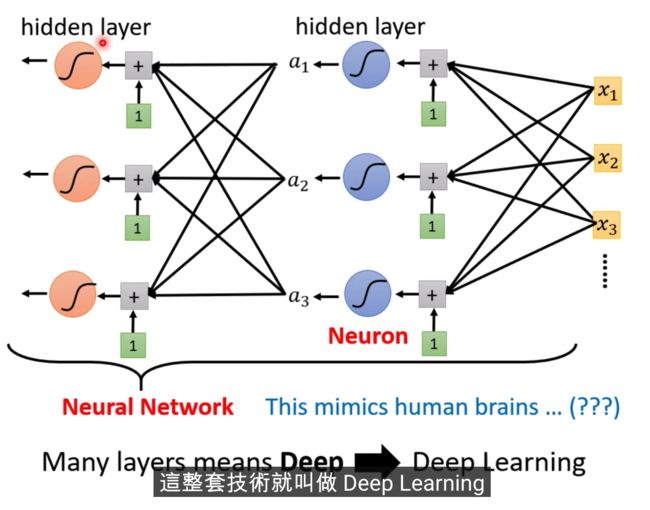
这个是在模拟人脑
Deep Learning的由来。。。。
只要有足够多的ReLU或者Sigmoid,就能够逼近任何连续的Function
反复用的意义在哪里?
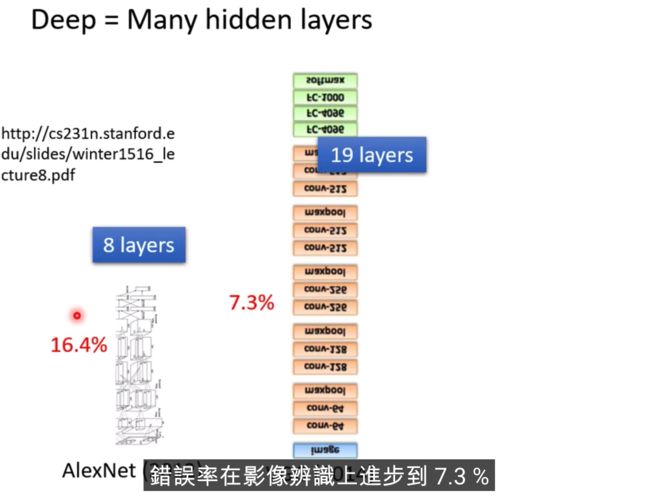
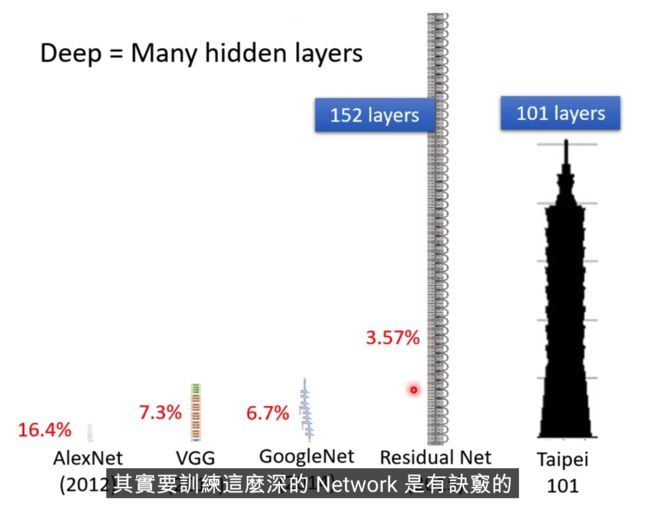
过多的层数效果不一定好
神经网络结构那部分讲的太精彩了。从简单的线性回归开始,到用几个简单线性函数去逼近一个分段线性函数,然后提出用sigmooid和线性逼近曲线,然后自然而然引出神经网络的基本结构。输入特征,参数,激活函数..等等概念自然而然都出来了