【机器学习】线性判别分析

一、原理

对于LDA 如何找到最佳投影线性变换矩阵

LDA（Linear Discriminant Analysis）和PCA（Principal Component Analysis）区别

二、示例代码

2.1 自定义实现lda算法对iris数据集进行降维

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt




def lda(X, y, dims):
    """
    线性判别分析算法 (LDA) 的实现


    参数:
        X: 数据矩阵, 形状为 (n_samples, n_features)
        y: 标签向量, 形状为 (n_samples,)
        dims: 降维后的维度数量


    返回:
        X_new: 降维后的数据矩阵, 形状为 (n_samples, dims)
    """
    # 获取所有类别标签
    target_nums = np.unique(y)
    # 初始化类内散布矩阵 Sw 和 类间散布矩阵 Sb 的列表
    Sw_list, Sb_list = [], []
    # 计算总体均值向量
    X_mean = X.mean(axis=0)
    # 遍历每个类别
    for target in target_nums:
        # 获取该类别的数据子集
        Xi = X[y == target]
        # 计算该类别的数据个数
        Xi_nums = Xi.shape[0]
        # 计算该类别数据的均值向量
        Xi_mean = Xi.mean(axis=0)
        # 计算类内散布矩阵
        Sw_list.append((Xi - Xi_mean).T.dot(Xi - Xi_mean))
        # 计算类间散布矩阵
        Sb_list.append(Xi_nums * (Xi - X_mean).T.dot(Xi - X_mean))
    # 将列表转换为 NumPy 数组
    Sw_list, Sb_list = np.array(Sw_list), np.array(Sb_list)
    # 计算总的类内散布矩阵和类间散布矩阵
    Sw, Sb = Sw_list.sum(axis=0), Sb_list.sum(axis=0)
    # 计算用于降维的矩阵 W  
    S = np.linalg.inv(Sw).dot(Sb)
    eig_vals, eig_vecs = np.linalg.eig(S)#特征值分解，得到特征值和特征向量
    # 对特征值进行排序并取前 dims 个
    eig_vals_idx = np.argsort(eig_vals) #将 eig_vals 中的索引按照特征值的升序排列
    eig_vals_idx = eig_vals_idx[::-1] #将排序后的索引数组进行反转，得到一个降序排列的索引数组。这样，特征值较大的索引将位于数组的前面。
    eig_vals_idx = eig_vals_idx[:dims] #保留最大的 dims 个特征值对应的索引
    W = eig_vecs[:, eig_vals_idx] #使用最终选择的索引构建降维的线性变换矩阵 W
    # 将数据进行降维
    X_new = X.dot(W)
    # 返回降维后的数据
    return X_new


if __name__ == '__main__':
    # 加载鸢尾花数据集
    iris_data = load_iris()
    # 获取数据和标签
    iris_X = iris_data.data  # 数据矩阵, 形状为 (150, 4)
    iris_y = iris_data.target  # 标签向量, 形状为 (150,)
    # 进行 LDA 降维, 保留 2 个维度
    res_data = lda(iris_X, iris_y, 2)
    # 可视化降维后的数据
    plt.figure()
    plt.scatter(res_data[:, 0], res_data[:, 1], c=iris_y)
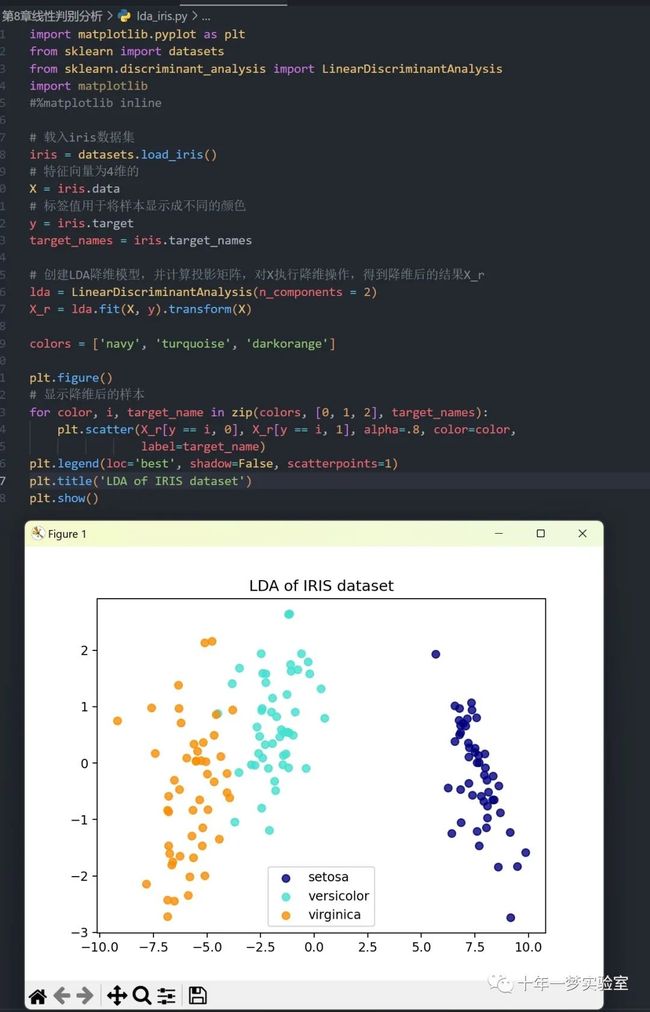
    plt.show()

2.2 调用sklearn的lda算法对iris数据集进行降维

2.3 使用sklearn的lda算法对手写数字数据集进行降维，并通过散点图进行可视化

# 导入库
import os
import matplotlib.pyplot as plt
import numpy as np
import sklearn.datasets
import sklearn.discriminant_analysis
import matplotlib
#%matplotlib inline


# 加载手写数字数据集，并限制类别数为 6
digits = sklearn.datasets.load_digits(n_class=6)


# 获取数据特征和目标标签
x = digits.data
y = digits.target


# 定义绘图函数
def plot_embedding(x, title):
    # 获取数据最大最小值
    x_min, x_max = np.min(x, 0), np.max(x, 0)
    # 对数据进行归一化
    x = (x - x_min) / (x_max - x_min)
    # 创建绘图对象
    plt.figure()
    # 定义颜色列表
    c = ['red', 'blue', 'lime', 'black', 'yellow', 'purple']
    # 遍历每个类别 
    for l in range(6): 
        # 获取该类别的样本
        p = x[y == l]
        # 绘制散点图
        plt.scatter(p[:, 0], p[:, 1], s=25, c=c[l], alpha=0.5, label=str(l))


    # 添加图例
    plt.legend(loc='lower right')
    # 隐藏坐标轴
    plt.xticks([])
    plt.yticks([])
    # 添加标题
    plt.title(title)
    # 显示图形
    plt.show()




# 复制一份数据
x2 = x.copy()
#  对数据进行微调，使其可逆，这是为了解决线性判别分析对奇异矩阵的敏感性
x2.flat[::x.shape[1] + 1] += 0.01
# 使用线性判别分析进行降维
x_lda = sklearn.discriminant_analysis.LinearDiscriminantAnalysis(n_components=2).fit_transform(x2, y)


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 绘制降维后的数据
plot_embedding(x_lda, '线性判别分析降维')

三、LDA应用概述

The End