TensorFlow拟合曲线问题及易错坑点

一、代码实现

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x_data_arr = np.linspace(-0.5, 0.5, 200)
x_data = x_data_arr[np.newaxis, : ]
noise = np.random.normal(0, 0.02, x_data.shape) 
y_data = x_data**2 + noise 

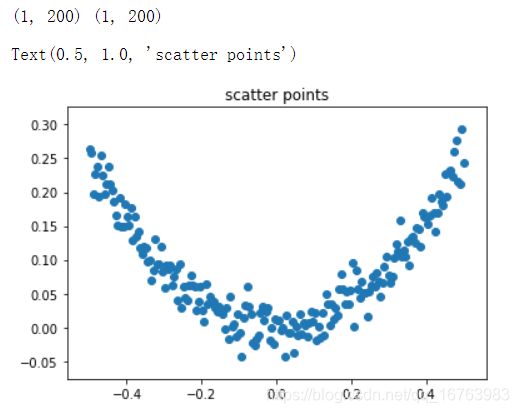
print(x_data.shape, y_data.shape)
plt.scatter(x_data, y_data)
plt.title("scatter points")

x = tf.placeholder(tf.float32, name = "x")  # 定义占位符
y = tf.placeholder(tf.float32, name = "y")

w1 = tf.Variable(tf.random_normal([10, 1]))  
b1 = tf.Variable(tf.zeros([10, 1])) 
z1 = tf.matmul(w1, x) + b1  
a1 = tf.nn.tanh(z1)  

w2 = tf.Variable(tf.random_normal([1, 10])) 
b2 = tf.Variable(tf.zeros([1, 1]))
z2 = tf.matmul(w2, a1) + b2
prediction = tf.nn.tanh(z2)

loss = tf.reduce_mean(tf.square(y - prediction))  
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) 

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer()) 
    for i in range(6000):
        sess.run(train_step, feed_dict={x: x_data, y: y_data}) 
        if i%1000 == 0:
            print(sess.run(loss, feed_dict={x: x_data, y:y_data}))
 
    prediction_y = sess.run(prediction, feed_dict={x: x_data}) 
    # 把矩阵squeeze为秩为1的数组，才能plt.plot
    prediction_y_squeeze = np.squeeze(prediction_y)
    x_data_squeeze = np.squeeze(x_data)
    # 画图
    plt.figure()
    plt.scatter(x_data, y_data) 
    plt.plot(x_data_squeeze, prediction_y_squeeze, c='r', lw=3)
    plt.title("curve")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.show()

二、plt中的矩阵转数组

在使用matplotlib.pyplot画图的时候，要注意plt.plot只能画一维数组，而不能画矩阵。
矩阵转秩为1的数组用如下代码：

x_squeeze = np.squeeze(x)

如果x和y是(1, 200)的矩阵，只能画散点图：

plt.scatter(x, y, c='r', s=1) 

如果要用plot画连续图像，需要先转化矩阵：

x_squeeze = np.squeeze(x)
y_squeeze = np.squeeze(y)
plt.plot(x_squeeze, y_squeeze, c='r', lw=5)

三、数组转矩阵

# np.linspace是生成一维数组，而神经网络需要的是矩阵
x_data_arr = np.linspace(-0.5, 0.5, 200)
# 在数组后加上[np.newaxis, :]表示转行向量，[: ,np.newaxis]表示转列向量
x_data = x_data_arr[np.newaxis, : ]

四、神经网络的维度问题

前向传播公式：
$$z^{[l]}=w^{[l]}{a}^{[l-1]}+b^{[l]}$$

$$a^{[l]}=g^{[l]}(z^{[l]})$$

反向传播：
tensorflow能一步实现，那就放心交给tf去求导优化吧！

用深度学习中的维度规律总结一下：
$$w^{[l]}:(n^{[l-1]},n^{[l]})$$

$$b^{[l]}:(n^{[l]},1)$$

$$z^{[l]}:(n^{[l]},1)$$

$$a^{[l]}:(n^{[l]},1)$$

好了，上面是关键，但是仅仅是维度基础，我想提的关键点在下面：
我看了很多篇关于曲线拟合的博文，都没有讲清楚初始化权重w和阈值b时的维度怎么得来的，有什么需要注意的地方。下面是我总结的一些编程注意点⚠

• 曲线拟合问题中有$x\to y$的映射，m个x对应m个y，用标准的深度学习思路来想这个问题：输入的x和输出的y都是(200, 1)矩阵，样本数量就是200，每个样本的维度是1，每个样本的那一列对应输出结果y矩阵的一个元素。
• 虽然说有m个样本时，$b^{[l]}:(n^{[l]},1)\to b^{[l]}:(n^{[l]},m)$，但是在代码中并没有把1换成200哟！这里是针对单样本而言的，当placeholder被真实数据替换后！才是向量化的开始。学习了深度学习的同学们不要把理论在实践中混淆使用咯！
• 初始化参数的维度代码：

w1 = tf.Variable(tf.random_normal([ n_x, n^[1] ]))
b1 = tf.Variable(tf.zeros([ n^[1], 1 ]))

z1 = tf.matmul(w1, x) + b
a1 = tf.nn.tanh(z1)