NR基础篇上——均值滤波、高斯滤波、双边滤波、NLM

人类的世界就是一个信号传输的世界，所以噪声无处不在，图像作为一种信号传输的方式当然也无法幸免。为了尽量减少噪声对图像质量的影响，还原物体的本来状态就提出了一系列降噪的方法，本文就简单介绍几种常见的降噪滤波算法。

图像噪声产生的原因

矫正方法

我将图像去噪的算法大致分位这么几类，包括硬件去噪，从源头降低噪声，常见的方式有CDS(cor related double sampling)，但是这种硬件的方式不是ISP涉及的范围所以不做过多介绍。然后就大致分位空域滤波、变换域滤波和时域滤波，当然还有一些其他方式比如空域和变换域相结合的方式，但是个人觉得大致这么分也可以。然后后面的算法会逐步更新，这篇主要几种讲解的是空域中的均值滤波相关的算法。

均值滤波

算法原理

如图是一个信号和噪声的分布图像，黑色曲线是真实信号，彩色的是多次采集的信号，会发现采集的信号是在真实信号上下波动，这个波动就是噪声对信号带来的影响。最早为了消除这种噪声有人就提出采用多张同一场景的图片求和取平均来消除，因为噪声是随机的，每张图中的噪声使得信号的偏移是不固定的，多次求平均后就能使得信号接近真实信号。就像上图中，对彩色的信号求平均相当于黑色曲线上下的值求平均，结果自然就接近黑色曲线从而达到去噪的效果。从多张叠加求平均的想法中有人就提出了从一张图里求平均来到达降噪的效果，也就是这里提到的均值滤波。其实整个算法的思想很简单，就是假设图像在一个很小的邻域范围内像素的变化不会太大，那么就可以在一个很小的邻域范围内求一个平均值来取代当前的像素值从而达到降噪的效果。典型的应用就是在图像中取一个3X3的邻域，然后每个像素给权重1，最后求和取平均。然后让这个邻域遍历整个图像。

用数学公式表示就是$f(i,j)=\frac{1}{9}\ast [f(i-1,j-1)+f(i-1,j)+f(i-1,j+1)+f(i,j-1)+f(i,j)+f(i,j+1)+f(i+1,j-1)+f(i+1,j)+f(i+1,j+1))]$

算法实现

%% --------------------------------
%% author:wtzhu
%% email:[email protected]
%% date: 
%% fuction: 均值滤波
%% --------------------------------
clear;
clc;
close all;
img = imread('./images/test_pattern_blurring_orig.tif');
[m, n] = size(img);
figure;subplot(221);imshow(img);title('original image');

%% 运算的时候需要对边缘进行扩展
% 需要特殊处理四周最外圈的行和列，本算法中将其向外扩展一圈，用最外圈的值填充
headRowMat = img(1,:);%取f的第1行
tailRowMat = img(m,:);%取f的第m行
% 行扩展后，列扩展时需要注意四个角需要单独扩展进去，不然就成了十字架形的
headColumnMat = [img(1,1), img(:,1)', img(m,1)];
tailColumnMat = [img(1,n), img(:,n)', img(m,n)];
expandImage = [headRowMat; img; tailRowMat];
expandImage = [headColumnMat; expandImage'; tailColumnMat];
expandImage = uint8(expandImage');
subplot(222);imshow(expandImage);title('expand image');

% 创建新的图像
newImg = zeros(m, n);
% 定义模板
meanKernal = uint8([1 1 1;
                    1 1 1
                    1 1 1]);
% 遍历图像进行均值滤波
% 1.首先提取图像中待操作的ROI
% 2.利用模板对提取的ROI进行运算并赋值给新的图像
for i =2: m+1
    for j =2: n+1
       imgRoi = [expandImage(i-1, j-1) expandImage(i-1, j) expandImage(i-1, j+1);
                 expandImage(i  , j-1) expandImage(i  , j) expandImage(i  , j+1);
                 expandImage(i+1, j-1) expandImage(i+1, j) expandImage(i+1, j+1)];
       newImg(i-1, j-1) = uint8(sum(sum(imgRoi.*meanKernal))/9);
    end
end
newImg = uint8(newImg);
subplot(223);imshow(newImg);title('new image');
subplot(224);imshow(img-newImg);title('newImg-img');

如图所示，第三幅图就是经过均值滤波处理后的效果，和第一幅图比起来变得更模糊。通过原始图像和新图像最差就能得到最后的图像，新清晰的看到边缘和部分噪点是被滤除掉了。所以这种降噪的方法有个致命的缺点就是会损失图像的边缘细节。

高斯滤波

算法原理

为了更好的保留边缘信息，就提出了加权平均的方法，就是平均之前每每个数的权重不一样。其实在图形中更好理解，某一个点的值肯定和本身的像素值关系最大，所以对应的本身哪个点的权重就会更大些，我么通过以下公式计算
$$\begin{array}{rl}f(i,j)& =\frac{1}{16}\ast [f(i-1,j-1)\ast 1+f(i-1,j)\ast 2+f(i-1,j+1)\ast 1+\\ & f(i,j-1)\ast 2+f(i,j)\ast 4+f(i,j+1)\ast 2+f(i+1,j-1)\ast 1+f(i+1,j)\ast 2+f(i+1,j+1)\ast 1)]\end{array}$$

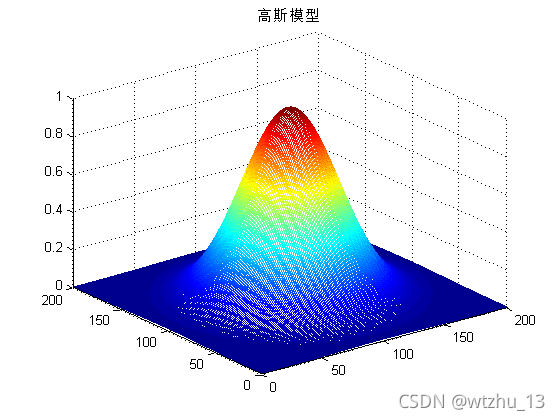
上面这幅图就是典型的高斯分布的图像，自然中很多分布都是满足高斯分布的，那么如果噪声也是高斯分布我们就可以通过高斯分布来进行加权。高斯滤波的具体思路如下：

• 使用与中心像素的距离，通过高斯函数来计算该点的权重；
• 将所有点的权重求出来后对权重进行归一化处理；
• 利用加权平均的方式计算滤波后的像素值；
• 邻域窗口遍历图像，重复上述操作。

整体思路和均值滤波没有太大区别，这里代码实现就不做过多叙述。

双边滤波

算法原理

虽然高斯滤波相对于普通均值滤波而言性能有所提升，但是依然对边缘随时严重，为了进一步保留边缘信息，就需要对边缘做进一步处理。于是就有人提出在高斯分布的基础上再加一个权重，这个权重和像素值的差别挂上联系，这个算法就是双边滤波算法。

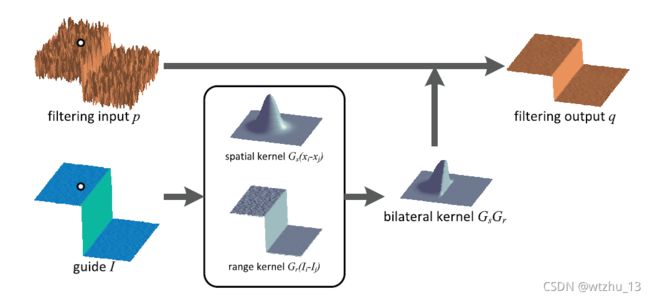
如图是原始论文中的公式，从中可以看出双边滤波有两个高斯权重叠加而来。前面||p-q||就是高斯滤波中使用的距离权重，后面的|Ip-Iq|就是像素值的高斯分布的权重。其实也很好理解，去噪的时候肯定需要相似的区域有更大的贡献，不相同的给小的权重，而对于边缘而言，那么两侧的像素值的差距肯定很大，也就会导致离边缘另一侧不同的会分配一个小权重，而同侧相差小就会有一个很大的权重，这样就不会由于取平均的时候将边缘两侧的大差异变小导致边缘变弱了，从而起到保留边缘的目的。

如图是双边滤波的示意图，当对白点位置进行滤波操作的时候，同侧像素差别较小会有一个大权重，而另一侧差别很大权重也就很小，二者结合后就相当于高斯滤波取一侧，然后利用这个核进行滤波操作。

算法实现

如图有很明显的边缘，我需要对红点处进行滤波

%% --------------------------------
%% author:wtzhu
%% email:[email protected]
%% date: 20211011
%% fuction: 双边滤波
%% --------------------------------
clc;clear;close all;

% gaussian filter
% the weight is only related to distance
x = 1:200;
y = 1:200;
[X, Y] = meshgrid(x, y);
D = (X-100).^2+(Y-100).^2;
z1 = exp(-D/2000);
figure();
mesh(x, y, z1)
title('高斯模型')

% add pixel value weight;
a = ones(200)*220;
a(:,1:100) = 20;
a(1:100,:) = 20;
figure();
imshow(uint8(a));
title('图像')
z2 = zeros(200);
for i=1:200
    for j=1:200
        z2(i, j) = exp(-(a(i, j)-220)^2/1800);
    end
end
figure();
mesh(x, y, z2);
title('像素权重');
z = z1.*z2;
figure();
mesh(x, y, z)
title('双边模型')

那么很容易就能得到一个高斯滤波的图形

然后根据像素差异通过高斯分布也很容易得到一个分布图像

因为我的图像中同侧像素是一样的，那么相当于权重都是1，另一侧相差接近最大位数控制，所以权重就很小接近0，所以才边缘的时候权重就会有一个阶跃的效果，然后把这两个权重相结合就可以得到一完整的滤波器

相当于我只对同一侧的像素进行一个高斯滤波，而另一侧则保留为原来的值，这样就能起到很好的保边效果。

NLM(non-local mean)

算法原理

前面的几种都是在邻域范围内对局部图像进行平均滤波，NLM则是利用整个图像的信息来进行降噪滤波处理。

如图是论文中的实例，对于p点而言，q1和q2点所在的邻域和p所在的邻域更相似，那么就给q1和a2较大的权重，而q3邻域和p邻域差别较大，就赋予一个较小的权重。具体权重的赋予方式其实也是高斯的一种方式，只不过e的对数是通过邻域简单欧拉距离来计算。

相当于求了几邻域中对应位置像素差的平方和来当作分配权重的依据。当邻域相似时，这个方差就小，权重也就大，而差异很大时方差就很大，权重也就很小，满足了算法的需求。理论上每一个点进行去噪的时候会利用整个图像的信息来计算，但是为了降低运算量，一般不会用整个图像的信息来计算，而是在整个图像中先选择一个大的范围，然后用这个范围内的点的信息进行降噪处理。

具体算法思路如下：

1. 遍历整幅图像；
2. 针对每一个点定义一个滑动窗口，降噪的时候利用该窗口中的所有点的信息计算；
3. 定义一个邻域范围，用来计算像素块的差异；
4. 遍历滑动窗口中的点，求每个点的邻域范围和当前点的邻域范围的像素差值的平方和，并利用该值计算一个权重；
5. 遍历完滑动窗口中的所有点后，滑动窗口中的每个点都有一个权重，对权重进行归一化处理；
6. 得到归一化处理后的权重通过加权平均的方式计算出当前点的新的像素值；
   

简化为图形就是如图的方式，最中间的黑色框的范围就是实际图像大小，外面蓝色范围时昨晚扩充的图像（为了处理边缘领域不够的问题）。计算黑色点的时候，就是定义一个红色框，然后黄色点在黄色框中遍历，每次都计算出两个小黑色框对应位置像素的差值的平方从而求出一个权重，当红色框遍历完了之后对权重机型归一化，然后加权平均就能求出黑色点的值。接着黑色点在图像中遍历，同事红色框随着黑点移动，然后黄色点又在红色框中移动，以此循环即可完成整幅图像的去噪操作。

算法实现

%% --------------------------------
%% author:wtzhu
%% email:[email protected]
%% date: 20211012
%% fuction: Non-Local Means
%% --------------------------------
close all;
clear all;
clc
img = imread('./images/lena.bmp');
I = double(img);
% I = double(imresize(img, [64, 64]));
figure();
imshow(uint8(I));
I_noise = I + 10 * randn(size(I));
figure();
imshow(uint8(I_noise));

% -----------------------------------
ds = 2;
Ds = 5;
h = 10;
% -----------------------------------

[m,n] = size(I_noise);
DenoisedImg = zeros(m,n);
PaddedImg = padarray(I,[ds+Ds,ds+Ds],'symmetric','both');

kernel = ones(2*ds+1,2*ds+1);
kernel = kernel./((2*ds+1)*(2*ds+1));
h2=h*h;

tic
for i=1:m
    for j=1:n
        num = 0;
        i1=i+ds+Ds;
        j1=j+ds+Ds;
        W1=PaddedImg(i1-ds:i1+ds,j1-ds:j1+ds);  % current window
        fprintf('=======current point: (%d, %d)\n', i, j);
        wmax=0;
        average=0;
        sweight=0;
        
        % search window
        % This window is not a fixed size, 
        % it shrinks when it's in the corner or border
        swmin = i1 - Ds;
        swmax = i1 + Ds;
        shmin = j1 - Ds;
        shmax = j1 + Ds;
        
        for r = swmin: swmax
            for s = shmin: shmax
                if(r==i1 && s==j1)
                    continue;
                end
                W2 = PaddedImg(r-ds:r+ds,s-ds:s+ds); % the window is to be compared with current window
                num = num + 1;
                % Use the mean directly in order to simplify the calculate
                Dist2 = sum(sum(kernel.*(W1-W2).*(W1-W2)));	
                w = exp(-Dist2/h2);   % the weight of the compared window
                if(w > wmax)
                    wmax = w;
                end
                sweight = sweight + w;  % sum the weight to normalize
                average = average + w*PaddedImg(r,s);
            end
        end
        fprintf('num of win: %d\n', num);
        average = average + wmax*PaddedImg(i1,j1);
        sweight = sweight+wmax;
        DenoisedImg(i,j) = average/sweight;
    end
end
figure();
imshow(uint8(DenoisedImg));
toc

我这里的带啊实现和算法原理和原始论文的代码有些许出入，主要时为了方便理解。原始代码中没有对图像进行扩充操作，而是在边界的时候，会做一个判断，通过改变滑动窗口的大小和邻域的半径来处理，初次看代码的时候可能不太好理解，所以我这里就没加这个，直接扩充后每个点的窗口和邻域大小都时一样的。

相关链接

• zhihu： ISP图像处理 - 知乎 (zhihu.com)
• CSDN：ISP图像处理_wtzhu_13的博客-CSDN博客
• Bilibili：食鱼者的个人空间_哔哩哔哩_Bilibili
• Gitee：ISPAlgorithmStudy: ISP算法学习汇总，主要是论文总结 (gitee.com)