王树森深度强化学习 笔记
本笔记基于王树森的深度强化学习课程
文章目录
- 王树森深度强化学习 笔记
-
- 一、基础
-
- 1. 概率论
- 2. 名词
- 3. Return U t U_t Ut
- 4. Action-Value Function Q π ( s , a ) Q_\pi(s, a) Qπ(s,a)
- 5. State-Value Function V π ( s ) V_\pi(s) Vπ(s)
- 二、Value-Based Reinforcement Learning
-
- TD 算法 Temporal Difference Learning
- Multi-Step TD Target
- Deep Q Network (DQN)
- q-learning
- sarsa
- Double DQN
- dueling network
- 经验回放
- 三、Policy-Based Reinforcement Learning
-
- 策略梯度基本流程
- 带baseline的策略梯度
- Deterministic Policy Gradient (DPG)
- Stochastic Policy Gradient
- 四、Actor-Critic Methods
-
- 基本的actor-critic AC
- advantage actor-critic A2C
- 五、离散空间与连续空间
-
- 离散化
- 六、多智能体强化学习
-
- 基本概念
- 三种架构
王树森深度强化学习 笔记
一、基础
1. 概率论
我们通常用大写字母 X X X表示一个随机变量,用小写字母 x x x表示随机变量的某个观测值
概率密度函数PDF(Probability Density Function),表示连续型随机变量的概率分布, ∫ X p ( x ) d x = 1 \int_Xp(x)dx = 1 ∫Xp(x)dx=1
概率分布函数PMF(Probability Mass Function),表示离散型随机变量的概率分布, ∑ x ∈ X p ( x ) = 1 \sum_{x\in X}p(x) = 1 ∑x∈Xp(x)=1
如果x是一个随机变量,x的函数值是f(x),那么f(x)的期望是: E [ f ( x ) ] = ∫ X p ( x ) ⋅ f ( x ) d x E[f(x)] = \int_Xp(x) \cdot f(x) dx E[f(x)]=∫Xp(x)⋅f(x)dx 或 E [ f ( x ) ] = ∑ x ⊂ X p ( x ) ⋅ f ( x ) E[f(x)] = \sum_{x\subset X}p(x) \cdot f(x) E[f(x)]=∑x⊂Xp(x)⋅f(x)
2. 名词
强化学习的主角叫做agent,它采取的动作和所处的状态分别为action和state
策略函数 Policy function 是指在某种state下,agent采取某种action的概率 π ( s , a ) \pi (s, a) π(s,a),函数值范围为 [ 0 , 1 ] [0, 1] [0,1], π ( a ∣ s ) = P ( A = a ∣ S = s ) \pi(a|s) = P(A=a |S=s) π(a∣s)=P(A=a∣S=s)
奖励 Reward 是指采取动作后,环境给agent的奖励,它可能为正、可能为负、可能为0
状态转移 state transition 是指agent在某个状态采取某个动作后,可能发生的状态变化。它是随机的, p ( s ′ ∣ s , a ) = P ( S ′ = s ′ ∣ s = s , A = a ) p(s'|s,a) = P(S' = s'|s = s,A = a) p(s′∣s,a)=P(S′=s′∣s=s,A=a)
强化学习中的随机性来源有两个方面:策略函数随机选择action、采取动作后随机的状态转移。
3. Return U t U_t Ut
强化学习是agent和environment互动的过程。我们观测到状态 s t s_t st,然后根据策略 π ( a ∣ s ) \pi(a|s) π(a∣s)选择一个动作 a t a_t at并执行它,环境会给出一个新的状态 s t + 1 s_{t+1} st+1和奖励 r r r,agent的轨迹是一系列(state, action, reward):

定义 t 时刻的 t时刻的 t时刻的Reurn 等于未来所有奖励之和: U t = R t + R t + 1 + R t + 2 + R t + 3 + … + R n U_t = R_t +R_{t+1}+R_{t+2}+R_{t+3} +…+R_{n} Ut=Rt+Rt+1+Rt+2+Rt+3+…+Rn
由于现在的奖励可能比未来的奖励更重要,比如里面给我一百块显然比一年后再给我一百块更好,所以定义Discounted Return : U t = R t + γ R t + 1 + γ 2 R t + 2 + γ 3 R t + 3 + … + γ n R n U_t = R_t +\gamma R_{t+1}+\gamma^2R_{t+2}+\gamma^3R_{t+3} +…+\gamma^nR_{n} Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3+…+γnRn, γ \gamma γ是折扣因子,是我们设置的超参数/
很显然,Return 是随机的。
4. Action-Value Function Q π ( s , a ) Q_\pi(s, a) Qπ(s,a)
Q π ( s t , a t ) = E [ U t ∣ S t = s t , A t = a t ] Q_\pi(s_t, a_t) = E[U_t|S_t = s_t, A_t = a_t] Qπ(st,at)=E[Ut∣St=st,At=at]
5. State-Value Function V π ( s ) V_\pi(s) Vπ(s)
V π ( s t ) = E A [ Q π ( s t , A ) ] V_\pi(s_t) = E_A[Q_\pi(s_t, A)] Vπ(st)=EA[Qπ(st,A)], A A A是动作空间
V π ( s t ) = ∑ a π ( a ∣ s t ) ⋅ Q π ( s t , a ) V_\pi(s_t) = \sum_a \pi (a|s_t)\cdot Q_\pi(s_t, a) Vπ(st)=∑aπ(a∣st)⋅Qπ(st,a) 离散动作的计算公式
V π ( s t ) = ∫ π ( a ∣ s t ) ⋅ Q π ( s t , a ) d a V_\pi(s_t) = \int\pi (a|s_t)\cdot Q_\pi(s_t, a) da Vπ(st)=∫π(a∣st)⋅Qπ(st,a)da 连续动作的计算公式
二、Value-Based Reinforcement Learning
定义Optimal action-value function Q ⋆ ( s t , a t ) = m a x π Q π ( s t , a t ) Q^\star(s_t, a_t) = \mathop{max}\limits_{\pi}Q_\pi(s_t, a_t) Q⋆(st,at)=πmaxQπ(st,at)
Q ⋆ ( s t , a t ) Q^\star(s_t, a_t) Q⋆(st,at)是最优情况下的 U t U_t Ut,不管我们在当前或后面采取怎样的策略 π \pi π,最终的结果都不可能超过 Q ⋆ ( s t , a t ) Q^\star(s_t, a_t) Q⋆(st,at)
在价值学习中我们要训练的函数就是 action-value function Q ( s , a ) Q(s, a) Q(s,a),训练的目标是 Q ⋆ ( s , a ) Q^\star(s, a) Q⋆(s,a),采取的最佳动作就是 a ⋆ = a r g m a x a Q ⋆ ( s , a ) a^\star = \mathop{arg max}\limits_{a}Q^\star(s, a) a⋆=aargmaxQ⋆(s,a)
TD 算法 Temporal Difference Learning
TD-learning思想很简单,有局部基于真实观测的数据,它的可信度大于完全基于预测的数据。
比如现在有三个地点A、B、C,C是A和B路径上的一个点。我们预测从A到B需要Q(A, B) = 100 mins,从C到B需要Q(C, B) = 50 mins。
经过我们的实验,发现从A到C实际需要30mins,那么30+ Q(C, B) = 80相比于Q(A, B) = 100来说是一个更准确的估计,我们可以得到一个Loss L = 0.5 ( 100 − 80 ) 2 L = 0.5(100 - 80)^2 L=0.5(100−80)2,我们称80为TD target,我们称100 - 80 = 20这个结果为TD error
Multi-Step TD Target
Deep Q Network (DQN)
DQN是使用一个神经网络 Q ( s , a ; w ) Q(s,a;\bold{w}) Q(s,a;w)来估计 action-value function Q ( s , a ) Q(s, a) Q(s,a),我们基于TD算法来训练这个神经网络,从而得到Optimal action-value function Q ⋆ ( s t , a t ) Q^\star(s_t, a_t) Q⋆(st,at)的估计
下图是agent的动作过程

下图是 U t U_t Ut的公式
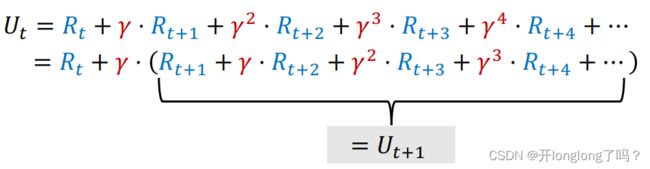
Q ( s , a ; w ) Q(s,a;\bold{w}) Q(s,a;w)函数其实就是 U t U_t Ut的估计, w \bold{w} w是神经网络的参数

我们做一下蒙特卡洛近似,把 A t + 1 , S t + 1 A_{t+1},S_{t+1} At+1,St+1替换为具体动作和观测到的状态,把 R t R_t Rt替换为具体观测到的奖励。
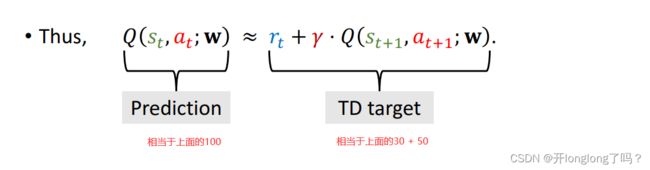
所以就得出了loss函数,然后对 w \bold{w} w做梯度下降即可,这样就完成了一次学习

总结一下,一次DQN的TD-learning迭代是这样的:

q-learning
q-learning学习的是最优动作价值函数,上面的DQN就属于q-learning的一种,所以这里只简要地总结一下q-learning

sarsa
sarsa与q-learning很像,唯一不同的是,sarsa所学习的是动作价值函数,它也可以用神经网络去估计动作价值函数。学习流程和DQN几乎一样,这里只简要总结一下:

Double DQN
我们定义一个target network,它与deep q network结构相同,但参数不同

Double dqn是指用target network做评估,用DQN做选择,可以有效防止过高的拟合

dueling network
我们定义optimal advantage function 优势函数 A ⋆ ( s , a ) = Q ⋆ ( s , a ) − V ⋆ ( s ) A^\star(s, a) = Q^\star(s,a) - V^\star(s) A⋆(s,a)=Q⋆(s,a)−V⋆(s)

可以得出下面这个公式,根据上面定义等式,两边同时对action a取max,可以很容易得到下面公式右边的最后一项等于0

之所以保留这个等于0的项,是因为后面做蒙特卡洛近似时会有用,可以防止出现训练出的网络不唯一的问题(这里我还没看懂)
依据上面的等式我们搭建三个神经网络来估计Q、V、A,Q神经网络参数是 w V w^V wV和 w A w^A wA,V的神经网络参数是 w V w^V wV,A的神经网络参数是 w A w^A wA

和DQN目的一样,我们训练过程是不断更新Q网络的参数,只不过DQN中Q网络的参数只有一个,而dueling network中Q网络的参数有两个也就是 w V w^V wV和 w A w^A wA。其余部分是完全相同的,我们怎么训练DQN,就怎么训练dueling netword。
经验回放
所谓的经验回放,就是我们把过去的经验存起来去多次利用。如下图所示,一次经验就是一次transition

TD error越大的经验,对我们来说是越重要的,我们应该更多地重复学习这些经验。所以在从经验池buffer里选择经验的时候,按照下面的策略:

三、Policy-Based Reinforcement Learning
策略梯度基本流程
用一个神经网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ)来估计策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s),其中 θ \theta θ是网络的参数。用 V ( s ; θ ) V(s;\theta) V(s;θ)来估计 V π ( s ) V_{\pi}(s) Vπ(s)。

把 V ( s ; θ ) V(s;\theta) V(s;θ) 对 θ \theta θ 求导,得到一个策略梯度,我们的目的是使 V ( s ; θ ) V(s;\theta) V(s;θ)越大越好,所以沿着这个梯度上升的方向去更新 θ \theta θ
经过一系列数学计算,策略梯度的计算结果是这样的:

这里就存在了一个问题,我们如何求 Q π ( s , A ) Q_\pi(s,A) Qπ(s,A)?,有两种方法。
第一种方法是执行普通的强化学习过程,,每当游戏结束的时候,用观测到的 U t U_t Ut来估计 Q π ( s , A ) Q_\pi(s,A) Qπ(s,A)的值

第二种方法是用一个神经网络来估计 Q π ( s , A ) Q_\pi(s,A) Qπ(s,A),然后执行强化学习过程来学习这个网络,这是后面会讲到的actor-critic methods
带baseline的策略梯度
定义一个baseline b b b,它是不依赖动作 A A A的,经过一系列数学推导可以得出下面的式子:

因为我们最后在实际计算的是无偏估计 g ( a t ) g(a_t) g(at),所以如何选择baseline是一件很重要的事情

我们对上面的策略梯队做蒙特卡洛近似,也就是用一个随机动作样本 a t a_t at来替换掉动作空间 A t A_t At,得到策略梯度的无偏估计 g ( a t ) g(a_t) g(at)
- 第一种选择,令 b = 0 b = 0 b=0,相当于不使用baseline,这就和上面策略梯度基本流程里的做法一样
- 第二种选择,让b等于状态价值, b = V π ( s t ) b = V_\pi(s_t) b=Vπ(st),为什么这样做呢?因为 V π ( s t ) V_\pi(s_t) Vπ(st)与动作空间 A A A无关,并且比较接近 Q π ( s , A ) Q_\pi(s, A) Qπ(s,A),也即 Q π ( s , A ) − b Q_\pi(s, A) - b Qπ(s,A)−b会更小,算法收敛会更快。
Deterministic Policy Gradient (DPG)
DPG是一种actor-critic方法,同样是训练策略网络 a = π ( s ; θ ) a = \pi(s;\theta) a=π(s;θ)和价值网络 Q = q ( s , a ; w ) Q = q(s, a;w) Q=q(s,a;w),但与前面不同的是,这里的动作网络输出不具有随机性,当输入一个状态 s s s,将输出一个确定的状态 a a a
Stochastic Policy Gradient
四、Actor-Critic Methods
基本的actor-critic AC
Actor-Critic Methods属于策略学习和价值学习的交集,因为既要学习策略网络 π \pi π,还要学习价值网络

基本的actor-critic methods是学习动作价值网络 Q Q Q,我们还是用TD算法去更新动作价值函数的参数 w w w,然后去更新策略函数的参数 θ \theta θ
算法流程如下图所示:

在训练过程中,我们用策略网络来指导agent的行为,用价值网络给策略打分、帮助策略网络做梯度上升。
训练结束后,我们用策略网络来选择策略,价值网络就用不到了。
advantage actor-critic A2C
A2C其实就是带baseline的AC方法,它的baseline b = V π ( s ) b = V_\pi(s) b=Vπ(s),于是我们学习的价值网络变成了 Q ( s , a ) − V π ( s ) Q(s, a) - V_\pi(s) Q(s,a)−Vπ(s),而这恰好是优势函数的定义式 A ( s , a ) = Q ( s , a ) − V π ( s ) A(s, a) = Q(s, a) - V_\pi(s) A(s,a)=Q(s,a)−Vπ(s),所以算法的名字叫advantage actor-critic。
五、离散空间与连续空间
离散化
和字面意思相同,把连续的动作空间离散化,得到离散动作空间。
比如我们可以把下面这个机械臂的动作空间离散化到一个二维网格中。

六、多智能体强化学习
基本概念
多智能体强化学习有四种常见的设定:
- Fully cooperative 各个agent的利益一致,获得的奖励相同,比如同一条生产流水线上的各个机器。
- Fully competitive 各个agent相互竞争,一方的收获是另一方的损失
- Mixed Cooperative & competitive 各个agent之间即存在合作也存在竞争,比如moba游戏中多人一队,队伍之间相互对抗,队伍内部相互合作。
- Self-interested 利己主义,是指每个agent只想最大化自己收益,至于别人收益的高低它不在乎
第 i i i个智能体的Discounted return U t i = R t i + γ R t + 1 i + γ 2 R t + 2 i + γ 3 R t + 3 i + … + γ n R n i U_t^i = R_t^i +\gamma R_{t+1}^i+\gamma^2R_{t+2}^i+\gamma^3R_{t+3}^i +…+\gamma^nR_{n}^i Uti=Rti+γRt+1i+γ2Rt+2i+γ3Rt+3i+…+γnRni
每个agent都有自己的policy network π ( a i ∣ s ; θ i ) \pi(a^i|s; \theta^i) π(ai∣s;θi)
第i个agent的state-value function V i ( s t ; θ 1 , . . . , θ n ) = E [ U t i ∣ S t = s t ] V^i(s_t;\theta^1,...,\theta^n) = E[U_t^i|S_t=s_t] Vi(st;θ1,...,θn)=E[Uti∣St=st]。注意,状态函数依赖所有玩家的策略网络参数 θ \theta θ,一个玩家改变策略会造成所有玩家收益变化
单智能体强化学习的目标是使 J ( θ ) = E S ( V ( S , θ ) ) J(\theta) = E_S(V(S,\theta)) J(θ)=ES(V(S,θ))
多智能体强化学习判断收敛的标准是纳什均衡,每个玩家都有自己的 J i ( θ 1 , θ 2 , . . . θ n ) = E S ( V i ( S , θ 1 , θ 2 , . . . θ n ) ) J^i(\theta^1,\theta^2,...\theta^n) = E_S(V^i(S,\theta^1,\theta^2,...\theta^n)) Ji(θ1,θ2,...θn)=ES(Vi(S,θ1,θ2,...θn)),如果对于任意一个玩家来说,如果其他玩家选择的策略不变,那么不能通过改变当前策略来提高 j i j^i ji值的话,就说明达到了nash均衡。
三种架构
三种架构分别为:
- Fully decentralized 完全去中心化: Every agent uses its own observations and rewards to learn its policy. Agents do not communicate.
- Fully centralized 完全中心化: The agents send everything to the central controller. The controller makes decisions for all the agents.
- Centralized training with decentralized execution: A central controller is used during training. The controller is disabled after training.
Fully decentralized 中每个agent单独训练自己的网络,它基于自己的策略网络采取动作,并观测动作发生后自己的状态和奖励,跟前面的单智能体强化学习一样

Fully centralized 由中心决定该做什么,中心有n个策略网络和价值网络,对应n个agents,它接收观测值来更新网络并决定动作。这样做的好处是中心知道所有的状态和价值,可以更好的训练网络和决定动作,坏处是速度会变慢。

Centralized training with decentralized execution,每个agent独立持有自己的策略函数,中心持有n个价值函数,对应n个agent。训练过程是中心化的,中心知道所有的观测状态、动作、奖励;训练结果是去中心化的,每个agent已经训练好了自己的策略函数,中心的价值函数就没必要存在了。
如下图所示,每个agent基于自己的策略函数采取动作,然后相关信息传给中心。

如图所示,中心接收到信息后,训练并调用q函数,计算q值返回给各个agent




