Machine learning

1# 本文所有内容都是有关Andrew老师视频资料知识总结，其中各模型案例均由python实现。
什么是机器学习？
——Arthur Samuel(1959)提出：“Field of study that gives computers the ability to learn without being explicitly programmed”

Unit1 Supervised Learning

meaning: Learns from being given “right answers”（学习输入、输出或X到Y的映射关系）

Regression（回归）: Predict a number; infinitely many possible outputs（无限多种可能）
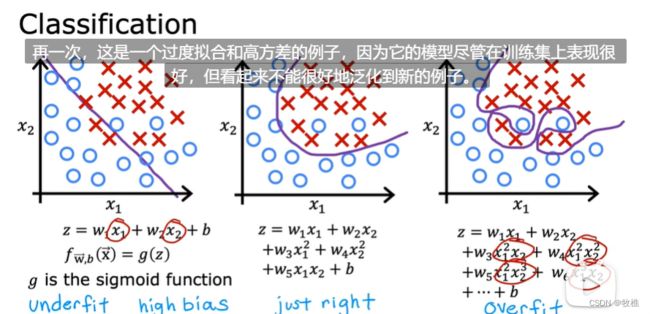
Classification（分类）： Predict categories; small number of possible outputs（只有几种可能）

Unit2 Unsupervised Learning

meaning: Find something interesting in unlabeled data.（Data only comes with inputs x, but not output labels y. Algorithm has to find structure in the data）

Clustering（聚类）: Group similar data points together;一种非监督算法，获取没有标签的数据并尝试自动将它们分组到集群中
Anomaly detection（异常检测）: Find unusual data points.
Dimensionality reduction（降维）: Compress data using fewer number

Uint3 Linear Regression Model（线性回归模型）

Training set: 表示输入的标准符号是小写的x，也成为输入变量，或特征/输入特征；表示尝试预测的输出变量（目标变量）的标准符号是小写的y；使用小写m表示训练示例的总数；为了表示单个训练示例，使用—（x,y）;可以在括号中给x,y加上标i,表示第i个训练示例。
training set----learning algorithm----f(hypothesis/function)[model]-----input “x”[feature]—output “y-hat”[prediction]

成本函数（Cost function）： J(w,b) 也称平方误差成本函数，取所有训练示例的误差平方和/2m。

上例是一个简化版的线性回归模型及其代价函数：b=0；此时代价函数J只与w有关，二维图形即可反应。

这是一个常规的线性回归模型，w和b同时变化，此时其代价函数用三维曲面表示，z轴表示J，J越小表示模型越准确，直观感受就是曲面的最底部，此时对应的w和b是最理想的模型参数。由上图表示对于同一个代价函数J值，可能对应多种不同的w、b值，相当于在代价函数图像中同一个水平面上所有点的J值相同，但w、b各不相同，相当于一个山顶的等高线。“等高线最中心处，即海拔最低处”代表了最理想的模型参数。但对于线性回归模型来说，只存在一个最低点，即全局最小值。

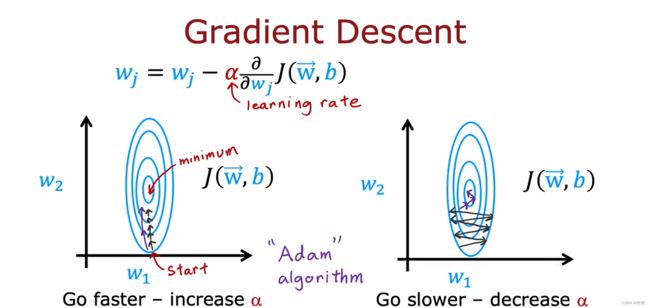
梯度下降（gradient descent）: 一种常见的找到最小成本函数参数的算法

通过为参数w和b选择起始值（一般从0，0开始）；然后判断从哪个方向“下坡”（即降低J值，让模型更精确），等到下一处地点（进行一次梯度下降过程后）再次判断，直到到达最低处（此时J值最小，即模型参数最理想）。因为起始点选择不同，梯度下降算法的结果也不相同，称为局部极小值。

梯度算法是根据上述公式不断更新w、b值实现的，即原始w值 - α*代价函数关于w的偏导数；b值同理；其中α为学习率，是一个0到1之间的数，表示w、b值改变的幅度，为常数。在之前描述的梯度算法实现中，每一次“下坡”就是改变一次w、b值，不管更新，直到代价函数J值最小。

注意： 每一次更新值时，需先计算出新的w、b值，在同时更新，不能先更新w值，再利用更新后的w值去计算新的b值，如上图所示。

继续以简化版的线性回归模型为例，此时b=0；当关于w的偏导数＞0，表示代价函数斜率＞0，根据梯度算法公式，更新后的w将会变得更小，根据图像反映，即越靠近最低点，实际意义表示为代价函数J值越小，模型更准确。如果w的偏导数<0,同理，更新后的w值会变大，也是更靠近最低点，模型更准确。

学习率（α）： 其值越小，则每次模型参数更新的幅度就缺小，达到最小J值需要更多步；其值越大，模型参数更新的幅度更大，就会造成一种情况，其更新的幅度越过了最小值，然后每次更新值都在最小值两边来回摇摆，逐渐远离理想值，不能收敛甚至可能发散。

exe1习题精讲

1.读取数据，为了方便将原始数据拷贝至同目录下

path = 'ex1data1.txt'
data = pd.read_csv(path,header=None, names=['Population','Profit'])

read_csv用于读取csv/txt等文本文件，path参数是路径；header与names是表格列名，配合使用：如果没有name参数，则将文件的某一行数据当作列名， 若header=0，则第一行数据变为列名，正文表格数据从第二行开始，（文本文件中的第二行数据变成表格第一行数据）若header=1，则第二行数据变为列名，正文表格数据从第三行开始（文本文件中的第三行数据变成表格第一行数据） 此时设置names，自定义列名，因此header=None即可，若=0/1/…则理论列名变化，但因为自定义了列名name， 所以等于先是数据变列名，然后再自定义列名覆盖前者，最终结果是自定义列名name，正文表格数据根据header参数值变化

data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8), color='r')
plt.show()

2.成本函数计算

def computeCost(X, y, theta):
    inner = np.power(((X*theta.T)-y), 2)
    return np.sum(inner)/(2*len(X))

3. 实现
   新增一列ones，用来记录theta变化情况

data.insert(0,'Ones',1) 

数据集增加一列x用来更新theta，‘Ones’表示新增列名；第一个参数是新增列位置，0表示第0列，因此新数据集第一列为Ones，第三个参数是数值。
结果: 新增了一列数值都为1，在第一列，列名为‘Ones’

4.初始化变量

'''初始化变量'''
cols = data.shape[1] #
'''
data.shape返回一个元组（x,y）:x为行数，为列数
data.shape[0]返回行数
data.shape[1]返回列数
下文需将训练集和目标变量分开，因此需要按列切片，所以shape[1]
'''

# iloc按索引检索；loc按名称检索
X = data.iloc[:,:cols-1]  # 保留所有行，列保留到最后一列（最后一列不要）
y = data.iloc[:,cols-1:cols]  # 保留所有行，列从2-3切片，也就是只要索引为2的列，也就是最后一列的目标变量

# 传入代价函数参数是矩阵，因此类型转换一下，表格变矩阵
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))

5. 梯度下降

def gradientDescent(X, y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X * theta.T) - y
        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            temp[0,j] = theta[0,j]-((alpha/len(X)) * np.sum(term))
        theta = temp
        cost[i] = computeCost(X, y ,theta)
    return theta,cost

初始化alpha，迭代次数为1500

alpha = 0.01
iters = 1500
g,cost = gradientDescent(X,y,theta,alpha,iters)
print(g) # 查看结果

6. 进行预测

# 预测35000和70000城市规模的小吃摊利润
predict1 = [1,3.5]*g.T
print("predict1: ", predict1)
predict2 = [1,7]*g.T
print("predict2: ", predict2)

7.拟合直线与cost变换可视化

x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0,0] + (g[0,1] * x)

# 原始数据与拟合直线
plt.subplot(1,2,1)
plt.plot(x, f,'r',label='Prediction')
plt.scatter(data.Population, data.Profit, label='Traning Data', s=10)
plt.legend(loc=2)
plt.xlabel('Population')
plt.ylabel('Profit')
plt.title('Predicted Profit vs. Population Size')


# 迭代次数与cost变换关系
plt.subplot(1,2,2)
plt.plot(np.arange(1500), cost, 'r')
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.title('Error vs. Training Epoch')
plt.show()

多元同理：

'''多参数'''
path2 = 'ex1data2.txt'
data2 = pd.read_csv(path2, header=None, names=["size", "bedrooms", "price"])
# print(data2)
# 特征值归一化
data2 = (data2- data2.mean()) / data2.std()
data2.insert(0,'Ones', 1)
cols2 = data2.shape[1]
traning_data_2 = data2.iloc[:,0:cols2-1]
targe_2 = data2.iloc[:,cols2-1:cols2]
# print(traning_data_2)
# print(targe_2)
X2 = np.matrix(traning_data_2.values)
y2 = np.matrix(targe_2)
theta2 = np.matrix(np.array([0,0,0]))
g2,cost2 = gradientDescent(X2, y2,theta2,alpha,iters)
print(g2)

Unit4 Multiple Linear Regression

with multiple features

4.1 vectorization

linear algebra: count from 1
code: count from 0

4.2 GradientDescent with multiple regression

Unit 4 Feature scaling

数据特征大小差距过大，导致成本函数图是一个个椭圆，在梯度下降过程中会来回波动，最后到达最低点，效率太低，

方法：
1.除以最大值；
2.均值归一化：原始数据可能都>0，均值均一化后可能是负
3.z-score归一化：

Unit5 Feature Engineering

根据问题情景，通过转换或者合并原始特征来设计一个新的验证

Unit6 Polynomial Regression

采用多元线性回归和特征工程的思想提出一种多项式回归新算法，可以将曲线、非线性函数拟合到数据中

6.1 Logistic Regression

6.2 Decision boundary

6.3 Cost function of LR

成本函数是整个训练集的函数，是单个训练示例的损失函数的平均值

6.4 GD Implementation

6.5 OverFitting

欠拟合=高偏差
过拟合=高方差

6.6 addressing overfitting

1. 获取更多的训练示例：通过更大的训练集，学习算法将会适应波动较小的函数。
2. 选择更少的特征：有很多特征，但训练集不足，会导致过拟合，进行特征选择
3. 正则化：估计算法缩小参数值，而没必要将参数值设置为0；即保留所有特征值

6.7 cost function with regularization

为了最小化原始成本，修改后的成本函数：均方误差函数+正则化项
两个作用：
1.尝试最小化第一项（均方误差）----更好的拟合训练数据
2.最小化第二项（正则化）—防止过度拟合

两个极端：
lamda=0：曲线过于复杂，此时过拟合
lamda=max：正则化权重较大，为了达到最小化，参数w都近乎为0，成本函数拟合为直线，此时欠拟合。

6.8 regularized linear regression

6.9 Regularized Logistic Regression

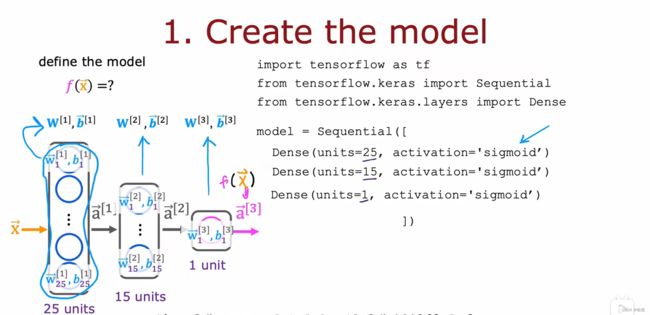
Unit7 Deep Learning

7.1 Neural network layer

前向传播：

Unit8 Tensorflow实现

8.1 Training Details

8.2 Activation Functions

8.3 Choose AF

8.4 Softmax

8.5 Adam

8.6 CNN

8.7 Computation Graph

Unit9 Diagnosis

9.1 Evaluation

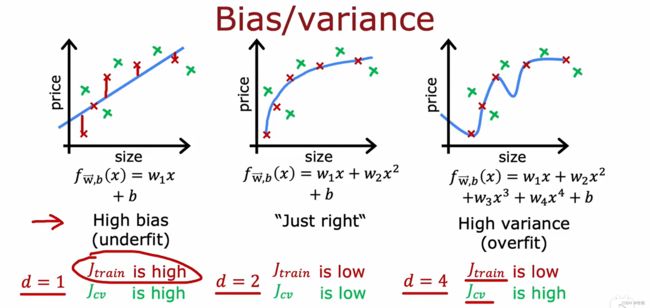
9.2 Bias and Variance

9.3 Learning Curves

对于一个二次成本函数，当训练样本很少的时候，很容易得到较小的训练误差，但训练样本很多的时候，二次函数很难拟合，因此训练误差会偏大。

对于具有高偏差的学习算法，随着训练样本的增多，训练误差会逐渐增大，然后趋于平滑，而交叉验证误差会逐渐下降，然后趋于平滑，但交叉验证误差始终大于训练误差，如果存在一个 人类水平表现，则一定在平滑训练误差的下方，两者间有一定的距离，这是“高偏差”的体现；因此对于具有高偏差的算法来说，越来越多的训练样本并不是更好拟合的方法；

对于具有高方差的学习算法来说，越来越多的训练样本是有效的，可以减小交叉验证误差

准确率： 所有预测为1的示例中实际分类为1的占比
召回率：在所有真实分类为1的示例中，我们正确预测的占比

高精准度意味着如果算法预测该患者患有某种疾病，则该患者极大可能真实患有该疾病；
高召回率意味着如果一个患者真患有某种疾病，该算法很大可能准确预测出患有该疾病

增大阈值，即将0.5提升为0.7，预测概率大于0.7时结果为1，小于0.7结果为0，不再是0.5。此时会提高精确度，但会降低召回率。表示为，我们只有在有很大可能确定该患者患有疾病时才会做出判断，因此精确度会提高，但有的确实患有疾病，而我们没有十足的把握确定，此时归类到不患有疾病中，因此召回率会降低。
减小阈值，将0.5降低到0.3，预测概率大于0.3的都为1，此时精确度降低，但召回率增大。实际含义为：为了确保每一位患者病情都被查出来，有点“宁可错杀100也不放过一个”的意思，只要有概率患病，哪怕只有0.3，我们都归类于患病，确保将所有病患都确诊，伴随的许多误诊，因此精确度会降低，但更多患者被确诊，因此召回率增大。

Unit 10 Decision Tree Model

10.1 measure pure

信息增益： 衡量由于分裂而导致树中熵的减少

10.2 Decision Tree Learning

1.从树的根节点处的所有训练示例开始，计算所有可能特征的信息增益，并选择要拆分的特征，从而提供最高的信息增益
2.根据选择的特征划分数据集，创造左右分支树
3.在左右子树重复该过程马，直到满足条件（某个节点100%，熵为0，树深度超过限制）

10.3 One hot encoding

回归树：

10.4 Sampling with replacement

构建一个新的训练集，放回随机抽样。

10.5 Random forest

假如有三个特征，在每个特征的子集中选择一个构成新的数据集，在生成决策树

Unit11 Cluster

一种无监督算法，没有标签，根据输入的数据特征自动分成几簇
常见的有k-meaning算法

11.1 K-meaning

1. 随即找两个点（自定义点数，以两个点做示例）作为簇中心，计算每个样本点到两个中心点的距离
2. 根据距离将所有点划分为两个区域，在计算每个区域中所有点的平均值
3. 将中心点移至平均点位处
4. 不断重复该过程
5. 直到将中心点移到新的平均位置后，再次划分的区域变化不大时完成分类
   

11.2 Optimization objective

11.3 Anomaly detection

另一种无监督算法，异常检测：给一定的训练集，判断新的测试集是否跟训练集特征不相同，也就是有异常。
常见的进行异常检测得是密度估计算法：在给定训练集（假定两种特征）时，先构建一种算法，找出训练集中最大概率出现的特征值，再找出出现概率最小的特征值

11.4 Gaussian Distribution

对于单个特征构建高斯模型；

对于多特征的训练集，对应特征概率相乘