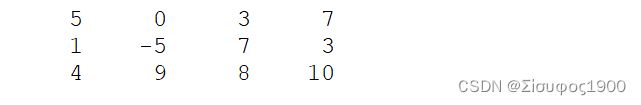协方差矩阵
协方差矩阵有什么意义? - 知乎
一、概述
最近一直在搞点云ICP 配准,里面用到了一个很重要的数学上东西就是协方差,由于面临的是两个点云之间的关系,那我们就需要研究一下协方差矩阵,后来慢慢的想了一些,之前我在做2D使用Halcon 的时候那个轮廓匹配、形状匹配、以及简单的那个灰度匹配的核心也是这个东西。其他领域的我们暂且不谈,就从点云匹配和2D匹配上就可以看出这个东西的重要性。
二、协方差矩阵
数学期望
数学期望(mathematic expectation)简而言之就是平均值。
协方差:
协方差表示两个变量的观测值对均值的偏离构成的向量的内积
概率密度是与观测值的出现次数成正比的,所以其实就是两个向量的内积。两个向量的夹角越小,说明两个变量越是正相关,两个向量夹角越大,说明两个变量越是负相关。其实两个向量的夹角的余弦值就是相关系数
协方差矩阵:
https://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5
特征:
1、协方差矩阵是一个方阵
2、协方差矩阵是一个对称矩阵
3、协方差矩阵的维度有列数来决定
协方差矩阵性质
协方差矩阵的意义:
因为协方差短阵表示向量两两之间的相似度,可以理解为向量之间的关系信息。协方差知阵保存的信息越多,误差越小。怎么保存更多信息呢?需要说明的是特征值代表特征向量的权重,所以挑最大的几个特征向量就能保存更多的信息,所以 协方差矩阵的最大特征向量能使得误差变小
Principal Component Analysis,PCA 的计算,然后排列特征值,从小到大的排列,可以计算数据的主要影响因素。
三、求解协方差矩阵
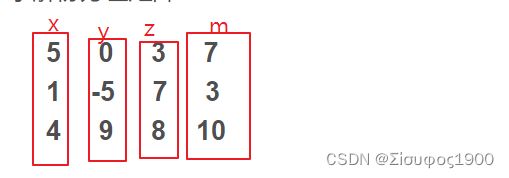
计算每一列的期望
x1=(5+4+1)/3= 3.3333
x2=(0+(-5)+9)/3=1.333
x3=(3+7+8)/3=6
x4=(7+3+10)/3=6.33333
计算每个的协方差
那么我可以计算
cov(x,x) =(pow(5-3.3333)+pow(1-3.3333)+pow(4-3.3333))/(3-1)=(2.7779+5.4443+0.4445)=4.3333
cov(x,y)=((5-3.3333)*(0-1.3333)+(1-3.3333)*(-5-1.3333)+(4-3.3333)*(9-1.3333))/2= 8.8333
cov(x,y)=((5-3.3333)*(3-6)+(1-3.3333)*(7-6)+(4-3.3333)*(8-6))/2=-3.0000
cov(x,m)=((5-3.3333)*(7-6.33333)+(1-3.3333)*(3-6.33333)+(4-3.3333)*(10-6.33333))/2=5.6667
第二行:
cov(x,y)=((5-3.3333)*(0-1.3333)+(1-3.3333)*(-5-1.3333)+(4-3.3333)*(9-1.3333))/2= 8.8333
cov(y,y)=((0-1.333)*(0-1.3333)+(-5-1.333)*(-5-1.3333)+(9-1.333)*(9-1.3333))/2= 50.3333
cov(y,z)=((0-1.333)*(3-6)+(-5-1.333)*(7-6)+(9-1.333)*(8-6))/2= 6.5000
cov(y,m)=((0-1.33333)*(7-6.333)+(-5-1.33333)*(3-6.33333)+(9-1.333)*(10-6.33333))/2= 24.1671
第三行:
cov(z,z)=((3-6)*(3-6)+(7-6)*(7-6)+(8-6)*(8-6))/2=7
cov(z,m)=((3-6)*(7-6.3333)+(7-6)*(3-6.3333)+(8-6)*(10-6.3333))/2=1
第四行:
cov(z,m)=((7-6.3333)*(7-6.3333)+(3-6.3333)*(3-6.3333)+(10-6.3333)*(10-6.3333))/2=12.333
所以组装一下:
matlab 代码
>> A = [5 0 3 7; 1 -5 7 3; 4 9 8 10];
>> C = cov(A)
C =
4.3333 8.8333 -3.0000 5.6667
8.8333 50.3333 6.5000 24.1667
-3.0000 6.5000 7.0000 1.0000
5.6667 24.1667 1.0000 12.3333
>> 到这里我就理解了点云哪里计算协方差的意义