双指针算法

介绍

双指针指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，一般分为两种，快慢指针，对撞指针。

快慢指针：两个指针开始在同一位置，一个移动快，一个移动慢。

对撞指针：两个指针分别在开头和结尾，向中间靠拢。

力扣 283.移动零（快慢指针）

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

提示:

• 1 <= nums.length <= 104
• -231 <= nums[i] <= 231 - 1

分析：这题一般最先想到的思路是遍历一遍数组，遇到0用后面的元素覆盖前面的元素，但这显然要两重循环，但这题使用双指针一重循环就可以了。

解题思路

首先要知道快指针和慢指针作用是什么，快指针是为了寻找新数组里面所需要的元素，慢指针对应的是新数组的下标，将快指针找到的值赋给新数组慢指针对应下表的空间里面，操作完后，再把零补齐。

代码如下：

#include
int main()
{
    int i, j = 0, numsSize, nums[100];
    scanf("%d", &numsSize);
    for (i = 0; i < numsSize; i++)
        scanf("%d", &nums[i]);
    for (i = 0; i < numsSize; i++)//i为快指针，j为慢指针
    {
        if (nums[i] != 0)
        {
            nums[j] = nums[i];
            j++;
        }
    }
    for (i = j; i < numsSize; i++)//补齐后面的0
        nums[i] = 0;
	return 0;
}

AC代码（力扣）(C)

void moveZeroes(int* nums, int numsSize) {
    int i,j=0;
    for(i=0;i

 

力扣 11. 盛最多水的容器（对撞指针）

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

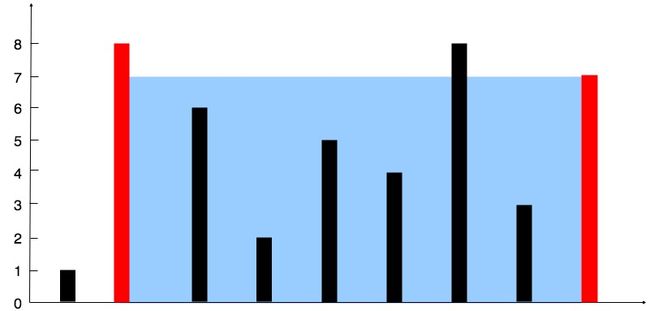
示例 1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

分析：这题同上题一样很容易想到两重循环，一个遍历左边界，一个遍历有边界，期间更新最大值，用双指针可以把两重降为一重循环。

解题思路

两指针分别位于头尾两侧，每次移动高度低的指针，为什么？两指针之间的距离变小了，若有效高度还不能增大，面积必然减小，移动期间更新最大值。

代码如下：

#include
int min(int a, int b)
{
    if (a > b)
        return b;
    else
        return a;
}
int main()
{
    int height[100], heightSize, i;
    scanf("%d", &heightSize);//输入有多少个柱子
    for (i = 0; i < heightSize; i++)
    {
        scanf("%d", &height[i]);//输入每个柱子的高度
    }
    int left = 0, right = heightSize - 1;//左指针，右指针赋初始值
    int max = (right - left) * min(height[left], height[right]);//初始面积
    while (left < right)//双指针移动
    {
        //移动高度低的指针
        if (height[left] < height[right])
            left++;
        else
            right--;
        //更新最大值
        if (max < (right - left) * min(height[left], height[right]))
            max = (right - left) * min(height[left], height[right]);
    }
    printf("%d",max);
	return 0;
}

AC代码（力扣）（C)

int min(int a,int b)
{
    if(a>b)
    return b;
    else
    return a;
}
int maxArea(int* height, int heightSize) {
    int left=0,right=heightSize-1;
    int max=(right-left)*min(height[left],height[right]);
    while(left