神经网络:激活函数层知识点
1.激活函数的作用,常用的激活函数有哪些
激活函数的作用
激活函数可以引入非线性因素,提升网络的学习表达能力。
常用的激活函数
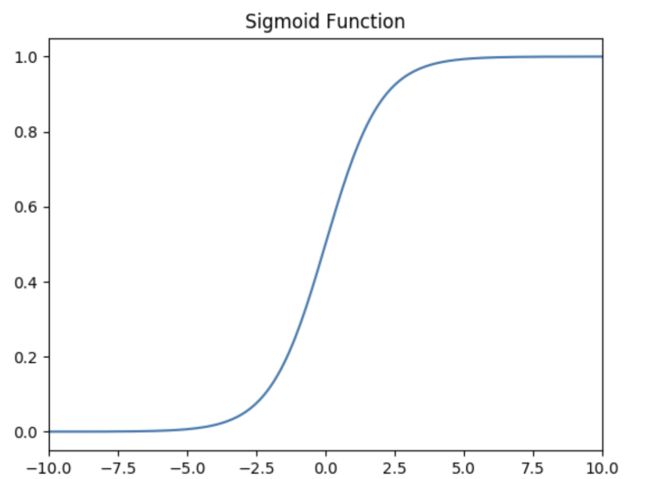
Sigmoid 激活函数
函数的定义为:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
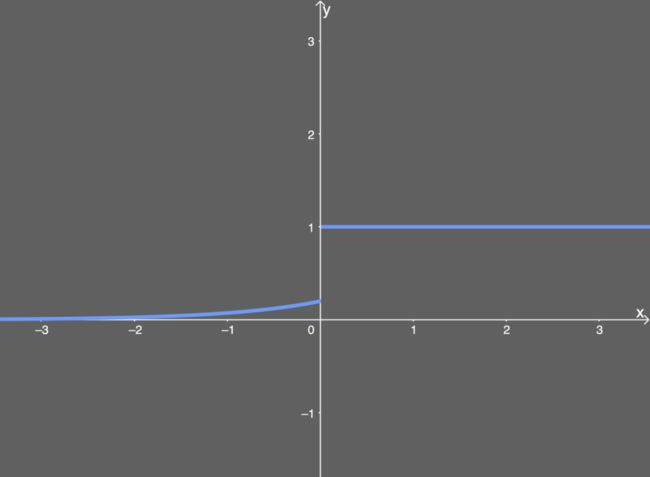
如下图所示,其值域为 ( 0 , 1 ) (0,1) (0,1) 。也就是说,输入的每个神经元、节点都会被缩放到一个介于 0 0 0 和 1 1 1 之间的值。
当 x x x 大于零时输出结果会趋近于 1 1 1 ,而当 x x x 小于零时,输出结果趋向于 0 0 0 ,由于函数的特性,经常被用作二分类的输出端激活函数。
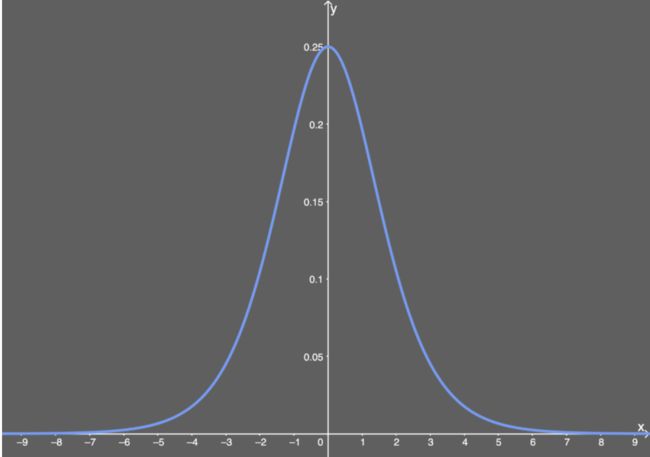
Sigmoid的导数:
f ′ ( x ) = ( 1 1 + e − x ) ′ = 1 1 + e − x ( 1 − 1 1 + e − x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x)=(\frac{1}{1+e^{-x}})^{'}=\frac{1}{1+e^{-x}}\left( 1- \frac{1}{1+e^{-x}} \right)=f(x)(1-f(x)) f′(x)=(1+e−x1)′=1+e−x1(1−1+e−x1)=f(x)(1−f(x))
当 x = 0 x=0 x=0 时, f ( x ) ′ = 0.25 f(x)'=0.25 f(x)′=0.25 。
Sigmoid的优点:
- 平滑
- 易于求导
- 可以作为概率,辅助解释模型的输出结果
Sigmoid的缺陷:
- 当输入数据很大或者很小时,函数的梯度几乎接近于0,这对神经网络在反向传播中的学习非常不利。
- Sigmoid函数的均值不是0,这使得神经网络的训练过程中只会产生全正或全负的反馈。
- 导数值恒小于1,反向传播易导致梯度消失。
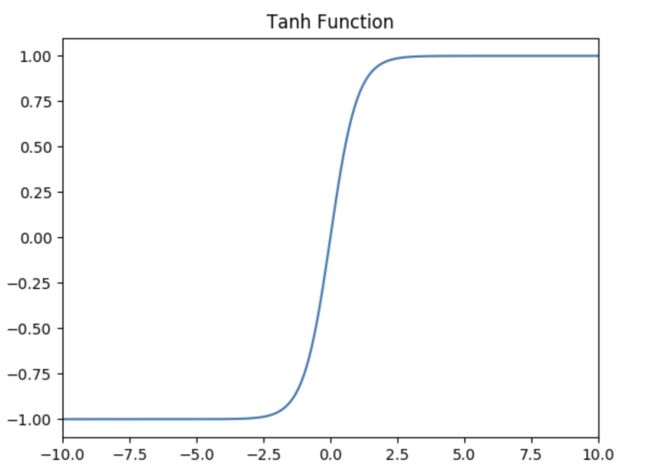
Tanh激活函数
Tanh函数的定义为:
f ( x ) = T a n h ( x ) = e x − e − x e x + e − x f(x) = Tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} f(x)=Tanh(x)=ex+e−xex−e−x
如下图所示,值域为 ( − 1 , 1 ) (-1,1) (−1,1) 。
Tanh的优势:
- Tanh函数把数据压缩到-1到1的范围,解决了Sigmoid函数均值不为0的问题,所以在实践中通常Tanh函数比Sigmoid函数更容易收敛。在数学形式上其实Tanh只是对Sigmoid的一个缩放形式,公式为 t a n h ( x ) = 2 f ( 2 x ) − 1 tanh(x) = 2f(2x) -1 tanh(x)=2f(2x)−1( f ( x ) f(x) f(x) 是Sigmoid的函数)。
- 平滑
- 易于求导
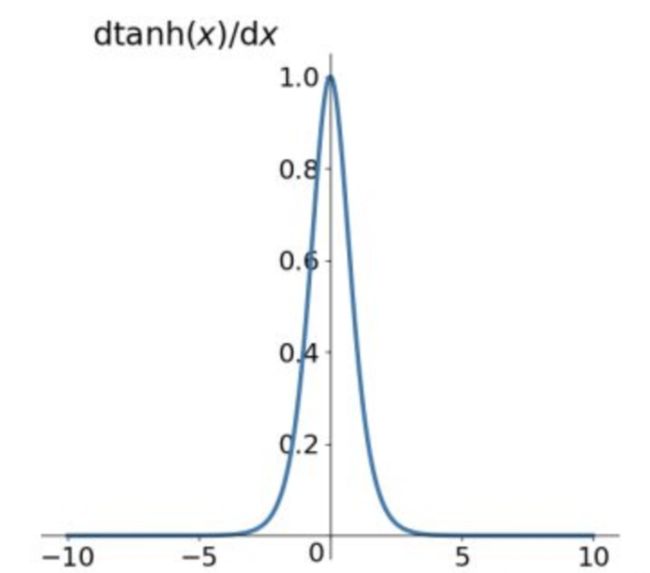
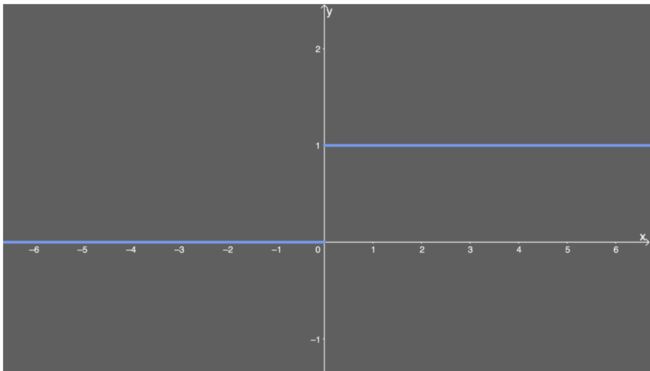
Tanh的导数:
f ′ ( x ) = ( e x − e − x e x + e − x ) ′ = 1 − ( t a n h ( x ) ) 2 f^{'}(x)=(\frac{e^x - e^{-x}}{e^x + e^{-x}})^{'}=1-(tanh(x))^2 f′(x)=(ex+e−xex−e−x)′=1−(tanh(x))2
当 x = 0 x=0 x=0 时, f ( x ) ′ = 1 f(x)'=1 f(x)′=1 。
由Tanh和Sigmoid的导数也可以看出Tanh导数更陡,收敛速度比Sigmoid快。
Tanh的缺点:
导数值恒小于1,反向传播易导致梯度消失。
Relu激活函数
Relu激活函数的定义为:
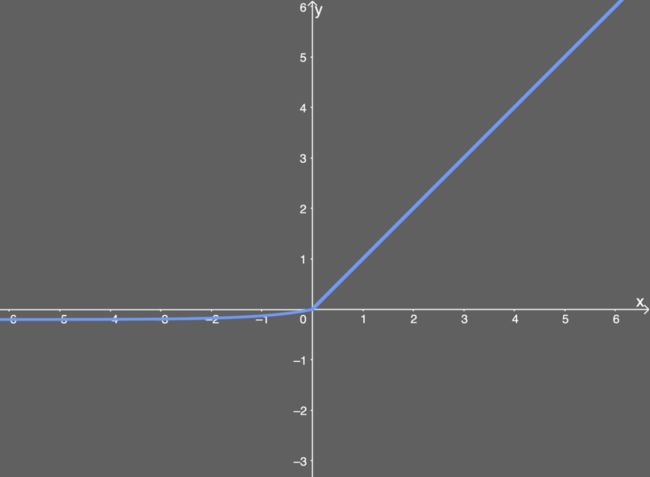
f ( x ) = m a x ( 0 , x ) f(x) = max(0, x) f(x)=max(0,x)
如下图所示,值域为 [ 0 , + ∞ ) [0,+∞) [0,+∞) 。
ReLU的优势:
- 计算公式非常简单,不像上面介绍的两个激活函数那样涉及成本更高的指数运算,大量节约了计算时间。
- 在随机梯度下降中比Sigmoid和Tanh更加容易使得网络收敛。
- ReLU进入负半区的时候,梯度为0,神经元此时会训练形成单侧抑制,产生稀疏性,能更好更快地提取稀疏特征。
- Sigmoid和Tanh激活函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度消失,而ReLU函数大于0部分都为常数保持梯度不衰减,不会产生梯度消失现象。
稀疏:在神经网络中,这意味着激活的矩阵含有许多0。这种稀疏性能让我们得到什么?这能提升时间和空间复杂度方面的效率,常数值所需空间更少,计算成本也更低。
ReLU的导数:
c ( u ) = { 0 , x < 0 1 , x > 0 u n d e f i n e d , x = 0 c(u)=\begin{cases} 0,x<0 \\ 1,x>0 \\ undefined,x=0\end{cases} c(u)=⎩ ⎨ ⎧0,x<01,x>0undefined,x=0
通常 x = 0 x=0 x=0 时,给定其导数为 1 1 1 和 0 0 0 。
ReLU的不足:
- 训练中可能会导致出现某些神经元永远无法更新的情况。其中一种对ReLU函数的改进方式是LeakyReLU。
- ReLU不能避免梯度爆炸问题。
LeakyReLU激活函数
LeakyReLU激活函数定义为:
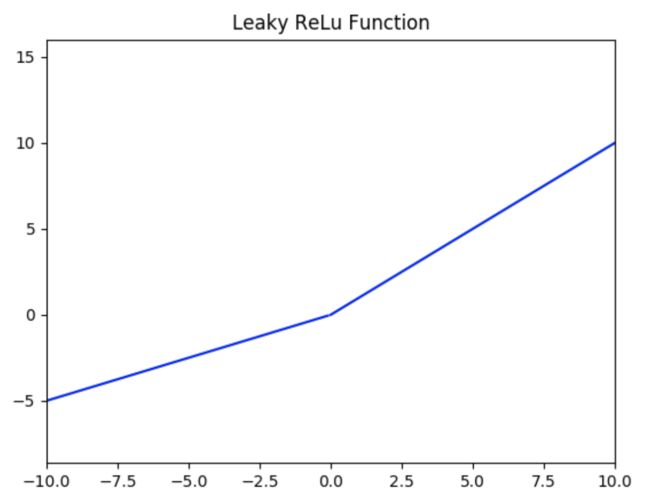
f ( x ) = { a x , x < 0 x , x ≥ 0 f(x) = \left\{ \begin{aligned} ax, \quad x<0 \\ x, \quad x\ge0 \end{aligned} \right. f(x)={ax,x<0x,x≥0
如下图所示( a = 0.5 a = 0.5 a=0.5 ),值域为 ( − ∞ , + ∞ ) (-∞,+∞) (−∞,+∞) 。
LeakyReLU的优势:
该方法与ReLU不同的是在 x x x小于0的时候取 f ( x ) = a x f(x) = ax f(x)=ax ,其中 a a a是一个非常小的斜率(比如0.01)。这样的改进可以使得当 x x x 小于0的时候也不会导致反向传播时的梯度消失现象。
LeakyReLU的不足:
- 无法避免梯度爆炸的问题。
- 神经网络不学习 α \alpha α 值。
- 在求导的时候,两部分都是线性的。
SoftPlus激活函数
SoftPlus激活函数的定义为:
f ( x ) = l n ( 1 + e x ) f(x) = ln( 1 + e^x) f(x)=ln(1+ex)
值域为 ( 0 , + ∞ ) (0,+∞) (0,+∞) 。
函数图像如下:
可以把SoftPlus看作是ReLU的平滑。
ELU激活函数
ELU激活函数解决了ReLU的一些问题,同时也保留了一些好的方面。这种激活函数要选取一个 α \alpha α 值,其常见的取值是在0.1到0.3之间。
函数定义如下所示:
f ( x ) = { a ( e x − 1 ) , x < 0 x , x ≥ 0 f(x) = \left\{ \begin{aligned} a(e^x -1), \quad x<0 \\ x, \quad x\ge0 \end{aligned} \right. f(x)={a(ex−1),x<0x,x≥0
如果我们输入的 x x x 值大于 0 0 0 ,则结果与ReLU一样,即 y y y 值等于 x x x 值;但如果输入的 x x x 值小于 0 0 0 ,则我们会得到一个稍微小于 0 0 0 的值,所得到的 y y y 值取决于输入的 x x x 值,但还要兼顾参数 α \alpha α ——可以根据需要来调整这个参数。公式进一步引入了指数运算 e x e^x ex ,因此ELU的计算成本比ReLU高。
下面给出了 α \alpha α 值为0.2时的ELU函数图:
ELU的导数:
![]()
导数图如下所示:
ELU的优势:
- 能避免ReLU中一些神经元无法更新的情况。
- 能得到负值输出。
ELU的不足:
- 包含指数运算,计算时间长。
- 无法避免梯度爆炸问题。
- 神经网络无法学习 α \alpha α 值。