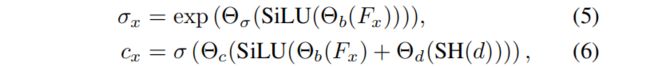【三维生成与重建】ZeroRF:Zero Pretraining的快速稀疏视图360°重建
系列文章目录
题目:ZeroRF: Fast Sparse View 360◦ Reconstruction with Zero Pretraining
任务:稀疏重建;拓展:Image to 3D、文本到3D
作者:Ruoxi Shi* Xinyue Wei* Cheng Wang Hao Su ,来自UC San Diego
code:https://github.com/eliphatfs/zerorf
文章目录
- 系列文章目录
- 摘要
- 一、前言
- 二、相关工作 & 预先知识
-
- 2.1 新视角合成
- 2.2 深度网络先验
- 2.3 稀疏视图重建
- 2.4 NeRF
- 2.5 TensoRF
- 三、本文方法
-
- 3.1 对特征Volume的分解
- 3.2 Generator 架构
- 3.3 Decoder 架构
- 四、实验
-
- 4.1 实验配置
- 4.2 数据集与指标
- 4.2 结果展示
- 4.3 分析
- 五、具体应用
-
- 5.1 Text to 3D 和 Image to 3D.
- 5.2 网格纹理和纹理编辑
- 2.读入数据
- 六、代码解析
-
- 1. 安装环境
- 2.Image-to-3D
- 扩展
-
- 1.morton3D编码
- 2.near_far_from_aabb:计算最近、最远点
- 3.march_rays_train
- 4. TV 正则化
摘要
ZeroRF,一种新的逐场景优化方法,用于在神经场中360°重建稀疏视图。当前,NeRF(神经辐射场)已经证明了高保真的图像合成,但难以使用稀疏的输入视图,且在数据依赖性、计算成本和跨不同场景的泛化方面都面临着限制。为了克服这些挑战,ZeroRF的关键是将一个tailored(裁剪的)深度图像优先集成到一个因子分解的NeRF表示中。与传统方法不同的是,ZeroRF使用神经网络生成器参数化特征网格,能够在没有任何预训练或额外的正则化的情况下实现高效的稀疏视图360°重建。并且可以延申到3D内容生成和编辑方面的应用。
一、前言
神经场表征的突破,如NeRF及其后续的发展实现了为高保真图像合成、加速优化和各种下游应用,却依赖于稠密的输入视图。特别当涉及到3D内容生成任务。因此,从稀疏的观点解决重建是一个显著的挑战。
近年来,稀疏视图重建[7,23,26,33,41,60,64,66,77]的方法越来越受关注。[7,28,33,77]的一种方法,通常被称为可推广的nerf,它依赖于具有大量时间和数据需求的广泛的预训练来直接重建感兴趣的场景。因此,这些模型的性能与训练数据的质量密切相关,由于大型神经网络的计算成本较高,其分辨率受到限制。此外,这些模型也很难在不同的场景中进行有效的推广。遵循逐场景优化范式的其他方法也包含了额外的模块,如视觉语言模型[23]和深度估计器[64]来帮助重建,在narrow baselines的方面证明有效,但在360°重建中性能不佳。此外,由于依赖额外的监督,对真实世界数据的适用性受到了限制,而这些监督可能并不总是可用的或准确的。人们还手工设计了跨越连续性[41]、信息论[26]、对称[51]和频率[73]正则化的先验。然而,额外的正则化可能会阻止NeRF忠实地重建场景[73]。此外,手工制作的先验往往不能适合相当微妙的设置变化。
此外,现有的360◦重建逐场景的优化方法,通常需要数小时的训练(即使在大型gpu上),与因子分解的Instant NGP[39]或TensoRF [8]等NeRF表示相比,收敛速度更慢,难以实际应用。
我们在NeRF合成数据集的Lego场景上,分别用4和100 视角,拟合了一个TensoRF [8],并在训练收敛后,从平面特征中可视化一个通道,如图2。
可以清楚地看到,在稀疏的4视图设置下,光线效应会产生噪声和扭曲的特征,而在密集(100)视图下,特征平面看起来完全像乐高的正交投影图像。我们在 triplane [6, 17] 和Dictionary Fields[9]表示上进行了类似的实验,发现这不是TensoRF特有的,而是这些基于网格的因子分解表示的普遍现象。因此可以假设在,稀疏视图监督下,如果因子分解特征保持干净,就可以实现快速的优化稀疏视图重构。
建议:将一个裁剪的深度图像先验[61]集成到一个因子分解的NeRF表示中(见图3)。ZeroRF没有像TensoRF、K-planes或Dictionary Fields[8,9,17]那样直接优化特征网格,而是用一个随机初始化的深度神经网络(生成器)来参数化特征网格。
这背后的直觉是,在不确定的监督下,神经网络在绝大多数情况下比查找网格概括得更好。更理论上讲,与容易感知和记忆[21,22,61]的数据相比,神经网络对噪声和伪影上具有更高的阻抗。该设计不需要任何额外的正则化或预训练,并且可以统一地应用于多种表示。参数化也是“无损”的,因为存在一组深度网络参数,从而可以实现任何给定的目标特征网格
ZeroRF作为一种新的逐场景优化方法,在不同的生成网络上进行了广泛的实验,以进行参数化和不同的分解表示,以找到最适合的组合稀疏视图360◦重建
- 不需要任何训练模型预,避免了对训练数据的任何潜在偏见,和对分辨率或相机分布等设置的任何限制;
- 训练和推理快速,因为它建立在分解的NeRF表示上,运行不到30秒;
- 与 underlying factorized 表示具有相同的理论表达力;
- 在网络合成[38]和开放照明[30]基准上使用稀疏视图输入,实现新视图合成的最新质量
鉴于ZeroRF具有高质量的360°重建能力,我们的方法可以应用于各个领域,包括3D内容的生成和编辑。
二、相关工作 & 预先知识
2.1 新视角合成
神经渲染技术为实现新视图合成中的逼真渲染质量铺平了道路:神经辐射场(NeRF)是第一个引入多层感知器(MLP),用于存储辐射场,并通过体渲染实现显著的渲染质量。后续,Plenoxels和DVGO 采用了基于体素的表示;TensoRF、Instant-NGP和DiF [9]提出了分解策略来加速训练;MipNeRF 和RefNeRF基于坐标的MLP,Point-NeRF 依赖于基于点云的表示。一些方法用有符号距离函数(SDF)[Neuralangelo、Unisurf、Permutosdf、Neus]代替密度场,或将密度场转化为网格表示[Mobilenerf、Neumanifold、Bakedsdf],以改善表面重建。这些方法可以提取出高质量的网格,而不会严重影响其渲染质量。此外,[3d gaussian splatting、4d gaussian splatting、Deformable 3d gaussians]的工作已经使用高斯飞溅来实现实时辐射场渲染
2.2 深度网络先验
虽然人们普遍认为,深度神经网络的成功是由于他们能够从大规模数据集中学习,但深度网络的体系结构,实际上在任何学习之前都捕获了大量的特征。
在随机卷积网络的特征上训练一个线性分类器可以产生比随机猜测[20]高得多的性能。随机初始化网络的特征也适合少数镜头学习者[1,18,50]。通过对这些随机特征的蒸馏,可以进一步推进先验,通过一系列自监督方法,包括BYOL [20],深度集群[5]和选择性伪标记[37],从这种归纳偏差开始,并使用不同的方法来提高图像表示学习。
与这些工作相比,深度图像先验[61]直接利用了这种深度先验,而无需进一步的蒸馏。结果表明,GAN生成器可以作为一种具有高噪声阻抗的参数化结构,因此可以应用于去噪、超分辨率和inpainting等图像恢复任务。这将进一步应用于各种成像和microscopy应用[36,43,54,55,62],并随着深度解码器[21,22]的理论和实际改进而扩展。ZeroRF遵循类似的范式,将深度先验嵌入到辐射场的参数化中。
2.3 稀疏视图重建
由于信息不足,NeRF在稀疏观测时表现出局限性。为解决挑战,一些方法在大量的数据集上,对[Mvsnerf、SRF、Sharf、Grf、pixelnerf]进行预训练,以传递先验知识,并在目标场景上微调模型。相反,另一种研究方法侧重于通过手动设计的正则化方法对每个场景进行优化[Putting nerf on a diet、Flipnerf、Mixnerf、 Geconer、Sparf、Freenerf]。例如,为了增加语义一致性,DietNeRF 使用CLIP视觉转换器提取高级特征。其中的许多设计损失函数来减轻交叉视图不一致,要么基于信息论。SPARF 利用预训练的网络进行对应或深度估计来弥补3D信息的缺乏。
2.4 NeRF
NeRF通过MLP表示一个三维场景辐射场:输入一个3D位置 x 和视图方向 d ,它输出体密度σx和与视图相关的颜色cx:

2.5 TensoRF
TensoRF替换了NeRF中的MLP,选择了一个特征 volume 来加快训练:它利用 CANDECOMP/PARAFAC 分解 或 VM分解将 特征volume 分解为因子。ZeroRF使用VM分解:给定一个三维张量T∈RI,J,K,它将一个张量分解为多个向量和矩阵:

其中vra 是向量因子,Mrb,c 是矩阵因子。
三、本文方法
ZeroRF管道如图3所示:使用冻结标准高斯噪声样本的深度生成器网络作为输入,以TensoRF-VM的方式生成平面和向量,形成一个分解的张量特征体。然后在渲染光线中对特征体进行采样,并由多层感知器(MLP)进行解码(标准的体渲染过程,损失为MSE)。
ZeroRF的主要思想是,应用未训练的深度生成网络,作为空间特征网格的参数化。网络可以从稀疏的观察学习不同规模的模式,自然推广到不可见视图,不需要进一步的上采样技巧或显式正则化,通常需要大量的人工调整,而不是之前的工作稀疏视图重建。
重要的设计如下:空间构成(特征体的表示),表示生成器的结构;以及特征解码器的结构。
3.1 对特征Volume的分解
应用深度生成网络进行参数化的原理,普遍适用于任何基于网格的表示。最直接的解决方案是直接参数化一个特征 Volume。然而,如果想要高渲染质量,特征Volume将特别大,占用内存且计算效率低。TensoRF 使用张量分解来利用特征卷的低秩性。当向量为常数时,[17]中使用的三平面表示可以看作是向量为TensoRF-VM表示的一种特殊情况。DiF将特征Volume 分解为多个编码不同频率的较小Volume。Instant-NGP[39]采用了多分辨率的hashmap,因为特征中的信息本质上是稀疏的。
在这些分解中,hash 打破了相邻单元之间的空间相关性,因此不能应用深度先验。深度生成网络可用于参数化(TensoRF、triplane和DiF)。
我们构建了用于生成一维向量、二维矩阵和三维体积的生成器架构,在此基础上我们实验了所有三种分解。由于工作原理类似,比以前的技术获得了更好的性能;TensoRF-VM性能最好,作为因子分解的最终选择。
3.2 Generator 架构
深度参数化的质量在很大程度上取决于框架。到目前为止,大多数Generator 都是Conv 和Attention 架构, 包括深度解码器(DD)、稳定扩散(SD)、变分自动编码器(VAE)、Kadinsky中的decoder,以及基于ViT解码器的SimMIM生成器。ZeroRF将二维卷积、池化和上采样层转换为一维和三维,以得到不同分解所需的相应的一维和三维Generator 。
这些生成器最初的体积相当大,因为它们被设计成适合于一个非常大的数据集,以生成高质量的内容。当涉及到单个NeRF场景时,这将导致不必要的长运行时间和较慢的收敛。幸运的是,我们发现,当我们缩小模型的宽度和深度时,收敛后的ZeroRF的性能保持不变。因此,我们保留了block的组成,但修改了这些架构的大小,以提高训练速度 。请注意, 在推理过程中,我们只需要存储辐射场表示,而不需要存储 Generator,因此在渲染过程中,ZeroRF与它的底层因子分解方法相比,其开销为零。
我们发现,SD VAE及其解码器部分,以及Kadinsky 解码器在新的视图合成中同样有效,其次是深度解码器,而SimMIM架构,作为辐射场的深度先验被证明是无效的。SD/Kadinsky编码器大多是卷积的原始结构,Kadinsky 在前两个区块中增加了自注意力。我们将(修改后的)SD解码器作为生成器架构的最终选择,因为它的计算量最少。
3.3 Decoder 架构
我们的解码器架构遵循SSDNeRF:用线性插值(双线性或三线性)从特征网格中进行解码,将其与第一个线性层投影, 得到密度和外观解码之间共享的基本特征代码。我们发现,共享特征代码可以通过耦合几何形状和外观紧密地帮助减少漂浮物。应用SiLU激活,并调用另一个线性层来进行密度预测。对于颜色预测,我们用球形谐波(SH)对视图方向进行编码,并将其通过线性层的投影添加到基本特征中,来添加视图依赖性。然后,我们应用SiLU激活,并使用另一个类似于密度预测的线性层来预测RGB值,表示如下:
Fx 是特征场, σ(·) 是sigmoid 函数,Θ• 是线性层。与TensoRF和DiF中使用的解码器不同,该解码器不消耗任何位置编码, 否则有可能泄露(深度先验之外的)位置信息,破坏或降低ZeroRF性能。
四、实验
4.1 实验配置
实验使用了AdamW优化器,β1=0.9,β2 =0.98,权重衰减0.2。学习速率从0.002开始,在余弦时间表下衰减到0.001。训练ZeroRF进行10k次迭代。体渲染过程中,我们对每条光线均匀采样1024个点,并采用 occupancy pruning 和 occlusion culling来加速这一过程。
4.2 数据集与指标
评估指标为PSNR、SSIM和 LPIPS;所有的输入视图都是通过在相机转换向量上运行KMeans ,并选择最接近集群质心的视图。
-
NeRF合成数据集:
NeRF-合成数据集包含8个不同材料和几何结构的对象。实验采用使用4或6个视图作为输入,并在200个测试视图上对模型进行评估。 -
OpenIllumination数据集:
一个灯光级的真实数据集,单一照明下复杂几何图形的8个对象,从38个训练视图中提取4或6个视图,并对10个测试视图进行评估。
- DTU 数据集:
DTU主要关注forward-facing 的对象,而不是360◦的重建,但为了完整起见,我们将我们对DTU的结果包含在图6中。我们使用3个视图作为输入,并在其余的视图上测试模型
4.2 结果展示
与最先进的 few-shot NeRF 方法对比:
1.RegNeRF :基于连续性和预训练RealNVP正则化,
2.DietNeRF:使用预训练CLIP模型
3.InfoNeRF:使用熵作为正则化器
4.FreeNeRF:基于频率正则化
5.FlipNeRF:使用空间对称先验
大多数基线模型都表现出不同程度的明显缺陷,包括 floater 和合成结果中明显的颜色shift(在图中的红色方框中突出显示)。对于预训练的先验,RegNeRF先验模型没有在宽基线图像上进行训练,并且在360◦设置下无法重建对象;有趣的是,使用CLIP作为先验模型的DietNeRF在真实图像上比在合成图像上效果更好,这与CLIP的预训练数据分布一致。FreeNeRF和FlipNeRF在nerf合成上表现相对较好,但在OpenIllumination上失败。
4.3 分析
稀疏视图数量的影响。设计实验如图7:ZeroRF在稀疏视图上的base TensoRF表示有显著优势;当观点变得更密集时,ZeroRF仍然保持竞争力,尽管优势较小
特征Volume分解方法。我们将ZeroRF生成器应用于三平面、TensoRF和DiF,并在NeRF合成数据集(6 views 输入)上比较性能。结果如表3。生成器的inclusion 不断地改进了base 表示,并且都实现了最先进的性能。这表明,使用深度参数化的原则一般适用于 grid-based 的表示。
Generator 框架。表4比较了不同框架的西南功能,图8可视化了不同Generator 平面特征的一个通道。没有任何先验和直接优化的平面,特征具有高频噪音和可见视图边界。相比之下,SD解码器和 Kadinsky模型产生了干净和良好的特征。SimMIM的完全注意力ViT解码器采用patch划分,可以看到块状伪影。MLP假设在网格上有一个非常平滑的过渡,因此不能忠实地表示场景内容。总的来说,卷积架构产生的特性与场景最一致

噪音的重要性。输入噪声是先验的关键。将其替换为零初始化的可训练特性,框架将完全破坏(表4最后一行)。如果解冻噪声,没有观察到性能的提高——由于学习率与噪声的规模相比很小,因此噪声的结构在整个训练过程中保持不变。但它引入了额外的开销,并减缓了收敛速度。因此,我们在训练过程中保持噪音冻结。
五、具体应用
5.1 Text to 3D 和 Image to 3D.
考虑到ZeroRF强大的稀疏量重建能力,一个简单的想法是使用现有的模型来执行一致的多视图生成,并应用ZeroRF将稀疏视图提升到3D中。Image to 3D任务,使用Zero123++将单个图像提升到6个视图,在生成的图像上拟合一个ZeroRF。对于文本到3D,首先调用SDXL 从文本中生成图像,并应用前面描述的图像到3D过程。如图9所示,ZeroRF能够从生成的多视图图像中产生可靠的高质量的重建。在A100 GPU上拟合ZeroRF只需30秒。
5.2 网格纹理和纹理编辑
网格纹理和纹理编辑。ZeroRF也可以用提供的冻结几何形状,来重建外观:从mesh中的随机渲染4张图像,平铺成一个大的图像,并应用Instruct-Pix2Pix[4],根据文本提示来编辑图像。然后,在四张图像上拟合一个ZeroRF,并将颜色值bake 回mash表面。在这种情况下,拟合ZeroRF只需要20秒,如图10
2.读入数据
代码如下(示例):
data = pd.read_csv(
'https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv')
print(data.head())
该处使用的url网络请求的数据。
六、代码解析
1. 安装环境
首先安装python3.7和cuda11.x的环境:
# bashrc文件中,将默认cuda指向11.5
export PATH=/usr/local/cuda-11.5/bin:$PATH
export LD_LIBRARY_PATH=/usr/local/cuda-11.5/lib64:$LD_LIBRARY_PATH
# 创建环境
conda create -y -n ssdnerf python=3.7
conda activate ssdnerf
# 安装 PyTorch
conda install pytorch==1.12.1 torchvision==0.13.1 torchaudio==0.12.1 cudatoolkit=11.3 -c pytorch
# 安装 MMCV and MMGeneration
pip install -U openmim
mim install mmcv-full==1.6
git clone https://github.com/open-mmlab/mmgeneration && cd mmgeneration && git checkout v0.7.2
pip install -v -e .
cd ..
# 安装 SpConv
pip install spconv-cu114
# Clone this repo and install other dependencies
git clone <this repo> && cd <repo folder> && git checkout ssdnerf-sd
pip install -r requirements.txt
# 安装 InstantNGP依赖
git clone https://github.com/ashawkey/torch-ngp.git
cd lib/ops/raymarching/
pip install -e .
cd ../shencoder/
pip install -e .
cd ../../..
2.Image-to-3D
首先需要i使用Zero123++ (https://github.com/SUDO-AI-3D/zero123plus),对单张图像生成6视图RGBD。样例图如下:

执行如下代码(需要提前登陆wandb账户):
python zerorf.py --load-image=examples/ice.png
zerorf.py 代码解析
# 1.读入6张图像-----------------------------------------------
image = torch.tensor(numpy.array(Image.open(args.load_image)).astype(numpy.float32) / 255.0).cuda() # (960,640,4)
images = einops.rearrange(image, '(ph h) (pw w) c -> (ph pw) h w c', ph=3, pw=2)[None] # (1,6,320,320,4)
# 2.读入meta,生成每张图的pose(外参)-----------------------------------------------
BLENDER_TO_OPENCV_MATRIX = numpy.array([
[1, 0, 0, 0],
[0, -1, 0, 0],
[0, 0, -1, 0],
[0, 0, 0, 1]
], dtype=numpy.float32)
poses = numpy.array([(numpy.array(frame['transform_matrix']) @ BLENDER_TO_OPENCV_MATRIX) * 2
for frame in meta['sample_0']['view_frames']])
mata.json中预先保存了图像外参,具体数值见下图:
# 3.读入内参(外参)-----------------------------------------------
intrinsics = numpy.array([[focal_length, focal_length, x, y]] * n_views=6) # [350,350,160,160]*(6)
# 4.射线中采样batch(4096):self.ray_sample:-----------------------------------------------------
rays_o = cond_rays_o.reshape(num_scenes, num_scene_pixels, 3) # 320*320*6=614400 -> (1,614400,3)
rays_d = cond_rays_d.reshape(num_scenes, num_scene_pixels, 3) # 320*320*6=614400 -> (1,614400,3)
if num_scene_pixels > n_samples: # 总射线数 > 4096
sample_inds = [torch.randperm( target_rgbs.size(1), device=device
)[:n_samples if self.patch_loss is None and self.patch_reg_loss is None else n_samples // (self.patch_size ** 2)]
for _ in range(num_scenes)] # 614400 根射线中,随机选4096根
sample_inds = torch.stack(sample_inds, dim=0)
scene_arange = torch.arange(num_scenes, device=device)[:, None]
rays_o = rays_o[scene_arange, sample_inds] # (1,4096,3)
rays_d = rays_d[scene_arange, sample_inds] # (1,4096,3)
target_rgbs = target_rgbs[scene_arange, sample_inds] # (1,4096,4)
# 4.5 初始化 code
code = code.to(next(self.parameters()).dtype) # (1,3,8,20,20)初始化的全0向量
# 4.6 更新 code
for _ in range(update_extra_state):
self.update_extra_state(code, *extra_args, **extra_kwargs)
#----------------------------以下是VolumeRenderer中的decode过程:------------------------------------
# 5.prepro(code)过程,用于生成三为特征。重点代码为:
self.code_proc_buffer = self.code_proc_pr_inv(self.preprocessor(self.code_proc_pr(code))
# self.preprocessor:TensorialGenerator生成两个3D张量-----------------------------------------------------------
# 循环两次,通过随即噪声,生成两个Tensorial 3D张量 --> (2,524288=64^3)
class TensorialGenerator(nn.Module):
self.subs = nn.ModuleList([(Tensorial3D)(in_ch=8, out_ch=16, noise_res=4)]) # 这里可选Tensorial1D Tensorial2D
def forward(self, _):
r = []
for sub in self.subs:
sub_out = sub() # 从噪音生成特征:(1,16,32,32,32)
r.append(torch.flatten(sub_out, 1)) # (1,16,32,32,32)-> (524288)
return torch.cat(r, 1) # 循环两次,生成两个Tensorial 3D张量 --> (1,1048576)
## 其中,Tensorial3D网络随机生成噪声,其网络架构如下图:
6.生成密集采样的坐标---------------------------------------------------------------------------------------------------------------------------------
grid_size = 64
# 间隔采样
X = torch.arange(grid_size, dtype=torch.int32, device=device).split(S) # (64):[0,1,2,...]
Y = torch.arange(grid_size, dtype=torch.int32, device=device).split(S) # (64):[0,1,2,...]
Z = torch.arange(grid_size, dtype=torch.int32, device=device).split(S) # (64):[0,1,2,...]
for xs in X:
for ys in Y:
for zs in Z:
# 生成3D坐标
xx, yy, zz = custom_meshgrid(xs, ys, zs) # (64,64,64)
coords = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1), zz.reshape(-1, 1)],dim=-1) #(262144,3) 在[0~64)之间
# 0~26243的索引,并打乱顺序
indices = morton3D(coords).long() # [N=262144]
# indices: [0,4,32,36,256,260,288,292,2048,2052,2080,2084...262111, 262139, 262143]
xyzs = (coords.float() - (grid_size - 1) / 2) * (2 * self.bound / grid_size) # 归一化到(-1,1)
# 添加噪声
half_voxel_width = self.bound / grid_size # 1/64
xyzs += torch.rand_like(xyzs) * (2 * half_voxel_width) - half_voxel_width
# 7.point_decode-----------------------------------------------------------------------
输入:code(dens.color两个3D特征块: 2*(16,32,32,32)),针对xyzs(262144=64^3, 3)做特征插值,得到(262144,16)*2 输出
point_code = self.get_point_code(code, xyzs)
# self.get_point_code 具体展开如下:
class FreqFactorizedDecoder(TensorialDecoder):
def get_point_code(self, code, xyzs):
for i, (cfg, band) in enumerate(zip(preprocessor.tensor_config, self.freq_bands)):
start = sum(map(numpy.prod, preprocessor.sub_shapes[:i])) # 0
end = sum(map(numpy.prod, preprocessor.sub_shapes[:i + 1])) # 524288 = 16*32^3
got: torch.Tensor = code[..., start: end].reshape(code.shape[0], *preprocessor.sub_shapes[i]) # (1,16,32,32,32)
assert len(cfg) + 2 == got.ndim == 5, [len(cfg), got.ndim]
coords = xyzs[..., ['xyzt'.index(axis) for axis in cfg]] # (1,262144,3)
if band is not None:
coords = ((coords % band) / (band / 2) - 1)
coords = coords.reshape(code.shape[0], 1, 1, xyzs.shape[-2], 3) # (1,1,1,262144,3)
codes.append(
F.grid_sample(got, coords, mode='bilinear', padding_mode='border', align_corners=False)
.reshape(code.shape[0], got.shape[1], xyzs.shape[-2]).transpose(1, 2)
) # (262144,16)两次循环 got3D 特征不同
return torch.cat(codes, dim=-1)
8.然后是渲染:--------------------------------------------------------------------------------------------------
sigmas, rgbs = self.point_code_render(point_code, dirs=None)
上步得到的point_code特征,并未分开渲染颜色和密度:
# 8.1 公共特征point_code,渲染sigma---------------------------------------------------------------
base_x = self.base_net(point_code) # linear:(32,64)
base_x_act = self.base_activation(base_x) # Silu
sigmas = self.density_net(base_x_act).squeeze(-1) # linear:(64,1) ->(262144,1)
# 8.2 渲染RGB-----------------------------------------------------------------------------
if dirs is None:
rgbs = None
#
density_grid = sigma
mean_density = torch.mean(density_grid.clamp(min=0)) # - 0.977
density_thresh = min(mean_density, 0.05)
# 9. near_far_from_aabb
self.aabb:[-1,-1,-1,1,1,1], 具体函数见最后拓展
nears, fars = batch_near_far_from_aabb(rays_o, rays_d, self.aabb.to(rays_o), self.min_near) # (1,4096)(1,4096)
# 10.march_rays_train 采样渲染(这块封装成c语言了,代码可见拓展)
# 该代码接受光线的起点、方向、网格数据等作为输入,并根据特定的算法进行光线追踪,最终计算出光线与场景的交点及相关信息。这段代码是用于实现神经辐射场(NeRF)模型中的光线追踪部分。
xyzs = torch.zeros(M, 3, dtype=rays_o.dtype, device=rays_o.device)
dirs = torch.zeros(M, 3, dtype=rays_o.dtype, device=rays_o.device)
ts = torch.zeros(M, 2, dtype=rays_o.dtype, device=rays_o.device)
get_backend().march_rays_train(rays_o, rays_d, density_bitfield, bound, contract, dt_gamma, max_steps, N, C, H,
nears, fars, xyzs, dirs, ts, rays, step_counter, noises)
return xyzs, dirs, ts, rays
后续即将到来。。。
扩展
提示:这里对文章进行总结:
1.morton3D编码
Morton编码,也称为Z编码,是一种用于将多维空间中的坐标映射到一维空间的方法。它通过对坐标的各个位进行交错排列,以便在一维空间中保持邻近的坐标在编码后仍然是相邻的特性。这种编码方法通常用于空间索引、图形学和计算机图形学中,以便快速搜索和处理多维空间中的数据。当使用2D坐标进行Morton编码时,假设我们有一个点的二维坐标为(3, 5),其二进制表示分别为(011, 101)。Morton编码会将这两个二进制数进行交错排列,得到010111,即十进制的23。这样就将二维坐标映射到了一维空间中的一个数值。Morton编码的主要目的是在一维空间中保持邻近的坐标在编码后仍然是相邻的。
void morton3D(const at::Tensor coords, const uint32_t N, at::Tensor indices);
2.near_far_from_aabb:计算最近、最远点
void near_far_from_aabb(const at::Tensor rays_o, const at::Tensor rays_d, const at::Tensor aabb, const uint32_t N, const float min_near, at::Tensor nears, at::Tensor fars) {
具体步骤如下:
1.根据线程索引,计算出当前处理的射线索引n。
2.根据射线索引定位到对应的射线起点和方向。
3.计算射线与AABB在x、y、z三个轴上的相交参数。
4.根据相交参数计算出射线与AABB的近点和远点。
5.计算得到的近点和远点存储在nears和fars中。
这个核函数的原理是,利用CUDA的并行计算能力,对每条射线进行独立的计算,以加速计算过程。通过并行计算,可以同时处理多个射线,提高了计算效率。具体调用函数如下:
__global__ void kernel_near_far_from_aabb(
const scalar_t * __restrict__ rays_o,
const scalar_t * __restrict__ rays_d,
const scalar_t * __restrict__ aabb,
const uint32_t N,
const float min_near,
scalar_t * nears, scalar_t * fars
) {
// parallel per ray
const uint32_t n = threadIdx.x + blockIdx.x * blockDim.x;
if (n >= N) return;
// locate
rays_o += n * 3;
rays_d += n * 3;
const float ox = rays_o[0], oy = rays_o[1], oz = rays_o[2];
const float dx = rays_d[0], dy = rays_d[1], dz = rays_d[2];
const float rdx = 1 / dx, rdy = 1 / dy, rdz = 1 / dz;
// get near far (assume cube scene)
float near = (aabb[0] - ox) * rdx;
float far = (aabb[3] - ox) * rdx;
if (near > far) swapf(near, far);
float near_y = (aabb[1] - oy) * rdy;
float far_y = (aabb[4] - oy) * rdy;
if (near_y > far_y) swapf(near_y, far_y);
if (near > far_y || near_y > far) {
nears[n] = fars[n] = std::numeric_limits<scalar_t>::max();
return;
}
if (near_y > near) near = near_y;
if (far_y < far) far = far_y;
float near_z = (aabb[2] - oz) * rdz;
float far_z = (aabb[5] - oz) * rdz;
if (near_z > far_z) swapf(near_z, far_z);
if (near > far_z || near_z > far) {
nears[n] = fars[n] = std::numeric_limits<scalar_t>::max();
return;
}
if (near_z > near) near = near_z;
if (far_z < far) far = far_z;
if (near < min_near) near = min_near;
nears[n] = near;
fars[n] = far;
}
3.march_rays_train
该代码接受光线的起点、方向、网格数据等作为输入,并根据特定的算法进行光线追踪,最终计算出光线与场景的交点及相关信息。这段代码是用于实现神经辐射场(NeRF)模型中的光线追踪部分。
__global__ void kernel_march_rays_train(
const scalar_t * __restrict__ rays_o,
const scalar_t * __restrict__ rays_d,
const uint8_t * __restrict__ grid,
const float bound, const bool contract,
const float dt_gamma, const uint32_t max_steps,
const uint32_t N, const uint32_t C, const uint32_t H,
const scalar_t* __restrict__ nears,
const scalar_t* __restrict__ fars,
scalar_t * xyzs, scalar_t * dirs, scalar_t * ts,
int * rays,
int * counter,
const scalar_t* __restrict__ noises
) {
// parallel per ray
const uint32_t n = threadIdx.x + blockIdx.x * blockDim.x;
if (n >= N) return;
// is first pass running.
const bool first_pass = (xyzs == nullptr);
// locate
rays_o += n * 3;
rays_d += n * 3;
rays += n * 2;
uint32_t num_steps = max_steps;
if (!first_pass) {
uint32_t point_index = rays[0];
num_steps = rays[1];
xyzs += point_index * 3;
dirs += point_index * 3;
ts += point_index * 2;
}
// ray marching
const float ox = rays_o[0], oy = rays_o[1], oz = rays_o[2];
const float dx = rays_d[0], dy = rays_d[1], dz = rays_d[2];
const float rdx = 1 / dx, rdy = 1 / dy, rdz = 1 / dz;
const float rH = 1 / (float)H;
const float H3 = H * H * H;
const float near = nears[n];
const float far = fars[n];
const float noise = noises[n];
const float dt_min = 2 * SQRT3() / max_steps;
const float dt_max = 2 * SQRT3() * bound / H;
// const float dt_max = 1e10f;
float t0 = near;
t0 += clamp(t0 * dt_gamma, dt_min, dt_max) * noise;
float t = t0;
uint32_t step = 0;
//if (t < far) printf("valid ray %d t=%f near=%f far=%f \n", n, t, near, far);
while (t < far && step < num_steps) {
// current point
const float x = clamp(ox + t * dx, -bound, bound);
const float y = clamp(oy + t * dy, -bound, bound);
const float z = clamp(oz + t * dz, -bound, bound);
float dt = clamp(t * dt_gamma, dt_min, dt_max);
// get mip level
const int level = max(mip_from_pos(x, y, z, C), mip_from_dt(dt, H, C)); // range in [0, C - 1]
const float mip_bound = fminf(scalbnf(1.0f, level), bound);
const float mip_rbound = 1 / mip_bound;
// contraction
float cx = x, cy = y, cz = z;
const float mag = fmaxf(fabsf(x), fmaxf(fabsf(y), fabsf(z)));
if (contract && mag > 1) {
// L-INF norm
const float Linf_scale = (2 - 1 / mag) / mag;
cx *= Linf_scale;
cy *= Linf_scale;
cz *= Linf_scale;
}
// convert to nearest grid position
const int nx = clamp(0.5 * (cx * mip_rbound + 1) * H, 0.0f, (float)(H - 1));
const int ny = clamp(0.5 * (cy * mip_rbound + 1) * H, 0.0f, (float)(H - 1));
const int nz = clamp(0.5 * (cz * mip_rbound + 1) * H, 0.0f, (float)(H - 1));
const uint32_t index = level * H3 + __morton3D(nx, ny, nz);
const bool occ = grid[index / 8] & (1 << (index % 8));
// if occpuied, advance a small step, and write to output
//if (n == 0) printf("t=%f density=%f vs thresh=%f step=%d\n", t, density, density_thresh, step);
if (occ) {
step++;
t += dt;
if (!first_pass) {
xyzs[0] = cx; // write contracted coordinates!
xyzs[1] = cy;
xyzs[2] = cz;
dirs[0] = dx;
dirs[1] = dy;
dirs[2] = dz;
ts[0] = t;
ts[1] = dt;
xyzs += 3;
dirs += 3;
ts += 2;
}
// contraction case: cannot apply voxel skipping.
} else if (contract && mag > 1) {
t += dt;
// else, skip a large step (basically skip a voxel grid)
} else {
// calc distance to next voxel
const float tx = (((nx + 0.5f + 0.5f * signf(dx)) * rH * 2 - 1) * mip_bound - cx) * rdx;
const float ty = (((ny + 0.5f + 0.5f * signf(dy)) * rH * 2 - 1) * mip_bound - cy) * rdy;
const float tz = (((nz + 0.5f + 0.5f * signf(dz)) * rH * 2 - 1) * mip_bound - cz) * rdz;
const float tt = t + fmaxf(0.0f, fminf(tx, fminf(ty, tz)));
// step until next voxel
do {
dt = clamp(t * dt_gamma, dt_min, dt_max);
t += dt;
} while (t < tt);
}
}
//printf("[n=%d] step=%d, near=%f, far=%f, dt=%f, num_steps=%f\n", n, step, near, far, dt_min, (far - near) / dt_min);
// write rays
if (first_pass) {
uint32_t point_index = atomicAdd(counter, step);
rays[0] = point_index;
rays[1] = step;
}
}
4. TV 正则化
TV正则化,全称是Total Variation Regularization。TV正则化通过最小化图像的梯度幅度来实现对图像的平滑处理,
具体来说,对于一个二维图像,TV正则化可以通过最小化图像的梯度幅度来实现平滑处理。从而抑制图像中的噪声和细节。使图像变得更加平滑。TV正则化通常会被应用于优化问题的正则化项中,以平衡数据拟合和平滑度之间的关系。
对于NeRF(Neural Radiance Fields)等主要用于三维重建的方法,TV正则化有助于改善重建结果的质量。这是因为在三维重建中,由于数据的稀疏性和噪声等因素,重建结果往往会包含不必要的细节和噪声。
另外,TV正则化还可以帮助增强对深度学习模型的约束,有助于提高模型的泛化能力和抗噪声能力。因此,对于NeRF等三维重建任务,应用TV正则化有助于改善重建结果的质量,并提高模型的稳健性。