MATLAB画球和圆柱

1. 画球

修改了一下MATLAB的得到球的坐标的函数：

GetSpherePoint

function [xx,yy,zz] = GetSpherePoint(xCenter,yCenter,zCenter,r,N)
% 在[xCenter,yCenter,zCenter]为球心画一个半径为r的球,N表示球有N*N个面，N越大球的面越密集
if nargin <= 4 % 没有输入N，默认N是20，球总共有20*20个面
    [X,Y,Z] = sphere;
else
    [X,Y,Z] = sphere(N);
end
[X,Y,Z] = sphere;
xx = X * r + xCenter;
yy = Y * r + yCenter;
zz = Z * r + zCenter;
end

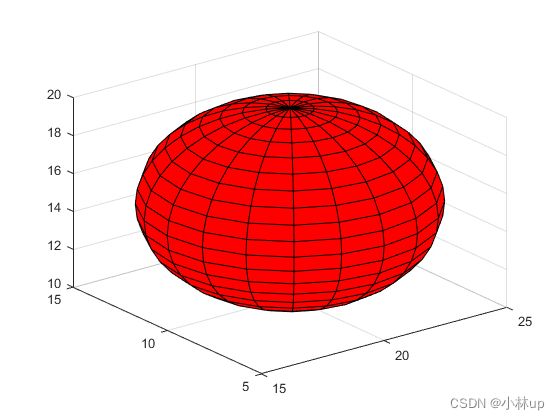
我们在(20,10,15)的地方画一个半径为5的球，调用上面的函数得到球上点的x、y、z坐标，这里没有设置N，默认的N是20：

 [xx,yy,zz] = GetSpherePoint(20,10,15,5);

绘制球：

surf(xx,yy,zz);

来换一个颜色：

[xx,yy,zz] = GetSpherePoint(20,10,15,5);
surf(xx,yy,zz,'FaceColor','r');

设置成100*100的面绘制：

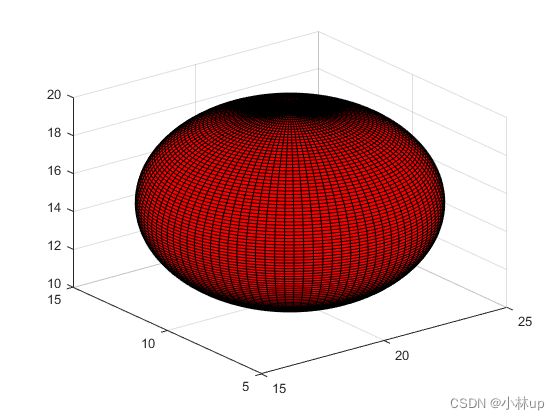
 [xx,yy,zz] = GetSpherePoint(20,10,15,5,100);
 surf(xx,yy,zz,'FaceColor','r')；

2. 画圆柱

绘制圆柱参考了MATLABcylinder的实现思路，但是cylinder只能绘制竖起来的圆柱，感觉使用比较受限，修改的函数可以生成任意形状的圆柱（包括倾斜的），这里需要知道的是圆柱的顶面和底面的圆心三维坐标，以及圆柱的半径，以及圆上的离散点数，先来看一下函数：

GetCylinderPoint

function [xx,yy,zz] = GetCylinderPoint(bottomCenterGlobalPoint, topCenterGlobalPoint, r, N)
% 第一个输入的参数是圆柱底部圆心点的空间坐标3*1，第二个输入的参数是圆柱顶部圆心点的空间坐标3*1，第三个输入的参数是圆柱的半径，第四个参数是圆柱圆平面的点数
% 返回值：所有的返回值都是2*N的矩阵，第一行是圆柱底面的边缘点的空间坐标，第二行是圆柱顶面的边缘点的空间坐标，xx是x的坐标，yy是y的坐标，zz是z的坐标

if nargin == 3 % 如果没有输入N，N和cylinder函数一样设置为20
    N = 20;
end
cylinderOrientation = (topCenterGlobalPoint - bottomCenterGlobalPoint)'; % 转换为一个行向量,由圆柱的底部指向空间的顶部的坐标轴
cylinderPlaneBasis = r * null(cylinderOrientation);
angle = [linspace(0, 2 * pi, N),0];
bottomEdgeGlobalVec = bottomCenterGlobalPoint + cylinderPlaneBasis(:,1) .* cos(angle) +  cylinderPlaneBasis(:,2) .* sin(angle);
topEdgeGlobalVec = topCenterGlobalPoint + cylinderPlaneBasis(:,1) .* cos(angle) +  cylinderPlaneBasis(:,2) .* sin(angle);
xx = [bottomEdgeGlobalVec(1,:);topEdgeGlobalVec(1,:)];
yy = [bottomEdgeGlobalVec(2,:);topEdgeGlobalVec(2,:)];
zz = [bottomEdgeGlobalVec(3,:);topEdgeGlobalVec(3,:)];

end

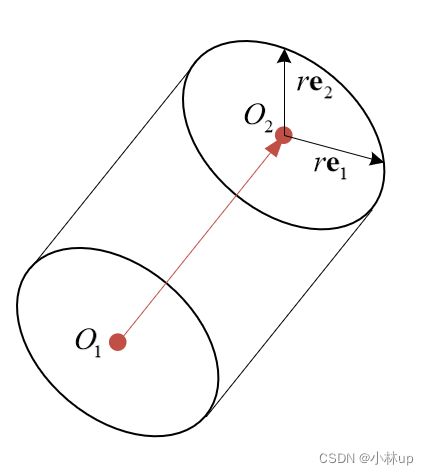
绘制的原理是：如图底面圆心和顶面圆心分别为$O_1$和$O_2$，它们会构成一个向量$O_1{O}_2$为代码的cylinderOrientation ，而圆柱的圆面是和$O_1{O}_2$垂直的，所以我们可以使用MATLAB的null函数找到圆面上的一对正交向量$r{\mathbf{e}}_1$和$r{\mathbf{e}}_2$，这里的$e_1$和$e_2$分别是单位向量，这两个正交向量的模长是r，也说明它们在圆周上。对应代码的cylinderPlaneBasis(:,1) 和cylinderPlaneBasis(:,2)，然后我们使用极坐标的方式，给定圆的离散点N，就可以把圆上所有的点的坐标得到：

• 离散角度：angle = [linspace(0, 2 * pi, N),0]最后要加一个0形成封闭否则圆柱少了一个面

• 平面上圆周上的点可以用两个正交向量来表示：$\mathbf{p}=r{\mathbf{e}}_1\cos \theta +r{\mathbf{e}}_2\sin \theta$，这里画画图很好理解
  

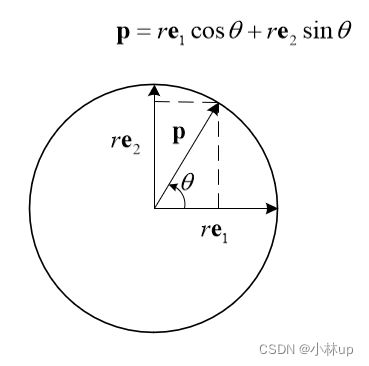
• 我们使用圆心的坐标加上上面的圆的坐标最后得到的就是我们想要的圆柱边缘的坐标了，对应上面的代码是：

bottomEdgeGlobalVec = bottomCenterGlobalPoint + cylinderPlaneBasis(:,1) .* cos(angle) +  cylinderPlaneBasis(:,2) .* sin(angle);
topEdgeGlobalVec = topCenterGlobalPoint + cylinderPlaneBasis(:,1) .* cos(angle) +  cylinderPlaneBasis(:,2) .* sin(angle);

ok，我们来检验一下：

我们知道圆柱底面圆的圆心的坐标是(1,3,4)，顶面圆心的坐标是(2,5,6)，圆柱的半径是5，这里的第四个参数圆的离散点数也没有给，默认是20，也就是说圆上有20个等距的点，然后我们先获取一下绘图的坐标：

[xx,yy,zz] = GetCylinderPoint([1;3;4], [2;5;6], 5)；

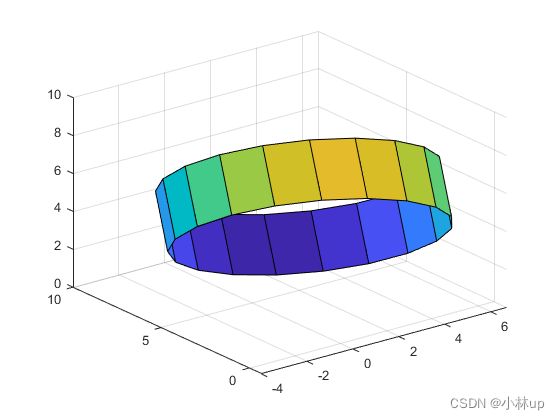
然后我们使用surf绘制一下圆柱：

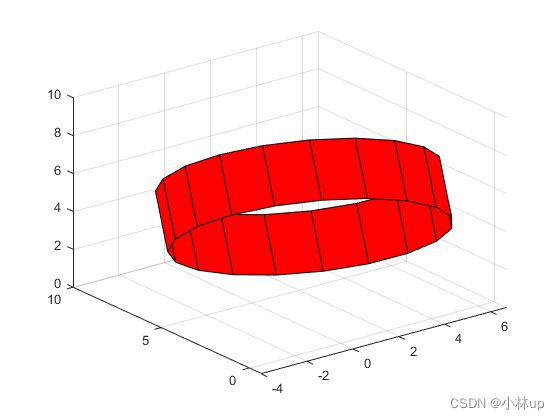
surf(xx,yy,zz);
view([-37.5,30])

来换一个颜色

[xx,yy,zz] = GetCylinderPoint([1;3;4], [2;5;6], 5);
surf(xx,yy,zz,'FaceColor','r');
view([-37.5,30])

我们把N设置为100来得到圆面用100个面绘制的圆柱：

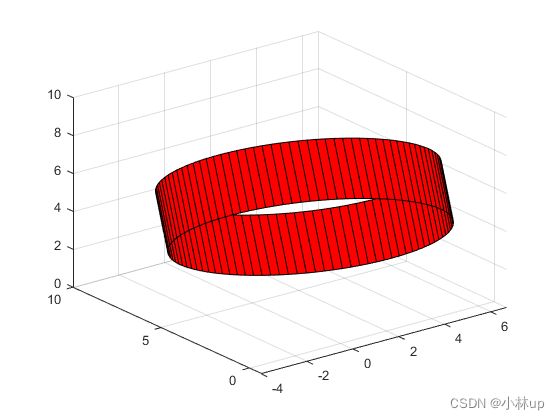
[xx,yy,zz] = GetCylinderPoint([1;3;4], [2;5;6], 5, 100);
surf(xx,yy,zz,'FaceColor','r');
view([-37.5,30])

我们可以把顶面和底面也涂上颜色：

[xx,yy,zz] = GetCylinderPoint([1;3;4], [2;5;6], 5,100);
figure;
hold on;
surf(xx,yy,zz,'FaceColor','r');
fill3(xx(1,:),yy(1,:),zz(1,:),'r');
fill3(xx(2,:),yy(2,:),zz(2,:),'r');
view([-37.5,30])

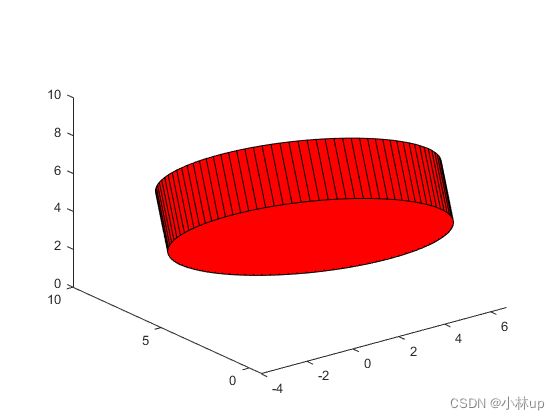
我们还可以把边缘的竖着的黑边全部去掉，添加'EdgeColor','none'即可：

[xx,yy,zz] = GetCylinderPoint([1;3;4], [2;5;6], 5,100);
figure;
hold on;
surf(xx,yy,zz,'FaceColor','r','EdgeColor','none');
fill3(xx(1,:),yy(1,:),zz(1,:),'r');
fill3(xx(2,:),yy(2,:),zz(2,:),'r');
view([-37.5,30])