Subtree of Another Tree

Problem

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

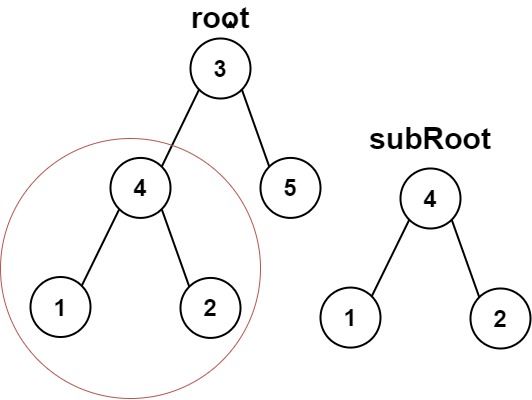
Example 1:

Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

Example 2:

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

Intuition

The problem is to determine whether two binary trees are the same or not. Two binary trees are considered the same if they are structurally identical, and corresponding nodes have the same values. The intuition is to perform a recursive comparison of nodes, checking if the current nodes are equal and then recursively comparing their left and right subtrees.

Approach

Base Cases:

If both trees are empty (None), return True since they are structurally identical.
If only one of the trees is empty, return False since they cannot be the same.
Node Value Comparison:

Compare the values of the current nodes in both trees.
If the values are not equal, return False.
Recursive Comparison:

Recursively compare the left and right subtrees of the current nodes.
The result of the comparison for the left and right subtrees should be True for the overall trees to be considered the same.
Return Result:

Return the result of the recursive comparison.

Complexity

• Time complexity:

The time complexity is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once during the recursive traversal.

• Space complexity:

The space complexity is O(h), where h is the height of the binary tree. This is due to the depth of the recursive call stack. In the average case, for a balanced binary tree, the height is O(log n), making the space complexity O(log n). However, in the worst case of an unbalanced tree, the height could be O(n), resulting in a space complexity of O(n).

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if not subRoot: return True
        if not root: return False

        if self.sametree(root, subRoot):
            return True
        return (self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot))


    def sametree(self, s, t):
        if not s and not t:
            return True

        if s and t and s.val == t.val:
            return (self.sametree(s.left, t.left) and self.sametree(s.right, t.right))
        return False