一份技术报告描述了一款用微透镜阵列修改的数码相机,它可以在一次曝光中捕捉部分的光场。作者展示了如何利用获得的光场来数字重新聚焦图像。论文“Fourier Slice Photography”,在2005年提出,包含了一个从光场成像的数学框架[Ng 05]。主要结果是一个新的定理,它将一幅图像作为光场的四维傅里叶变换的切片联系起来。 入射到相机主透镜表面的光是一个光场:在透镜上的每一点上,来自一组射线方向的辐射进入透镜。该方向集进一步受到孔径的限制,并且光线被透镜系统中的光学器件所折射,但传感器平面上的每个点最终接收到来自一组方向的辐射。到达传感器平面的一组光线被称为相机内的光场。图5.21说明了这个概念。传感器平面上的一个点(x,y)接收来自主透镜上由(u,v)参数化的一组点的辐射,尽管这种对应关系取决于相机的光学和聚焦状态。如果F是从透镜平面到传感器平面的距离,则从点(u、v)到(x、y)处的亮度用LF(x、y、u、v)表示。由于其他光学元件,包括孔径停止,可能没有光从透镜上的任意点(u,v)到任意点(x,y)的路径,在这种情况下,Lf(x,y,u,v)=0。
入射到相机主透镜表面的光是一个光场:在透镜上的每一点上,来自一组射线方向的辐射进入透镜。该方向集进一步受到孔径的限制,并且光线被透镜系统中的光学器件所折射,但传感器平面上的每个点最终接收到来自一组方向的辐射。到达传感器平面的一组光线被称为相机内的光场。图5.21说明了这个概念。传感器平面上的一个点(x,y)接收来自主透镜上由(u,v)参数化的一组点的辐射,尽管这种对应关系取决于相机的光学和聚焦状态。如果F是从透镜平面到传感器平面的距离,则从点(u、v)到(x、y)处的亮度用LF(x、y、u、v)表示。由于其他光学元件,包括孔径停止,可能没有光从透镜上的任意点(u,v)到任意点(x,y)的路径,在这种情况下,Lf(x,y,u,v)=0。
在传感器光点的数码相机内形成的图像的像素值理想地与穿过像素光点的时间积分通量成正比。对于足够小的像素,通量本质上只是辐照度,这是通过积分入射辐照度来计算的。辐照度是通过对方向半球上的入射辐射进行积分得到的。在相机计算中,跨透镜积分更明智,这需要改变透镜参数u和v的变量,类似于在渲染方程(见(计算机图形学的魔法的概述篇(一) 公式2.4))中应用的表面积分变换。
实际的积分依赖于一些内在的相机参数,以及一些额外的几何项。然而,在适当的假设下,光位点的辐照度可以近似为 这里A(u,v)是一个“光圈”函数,可以模拟相机光圈:如果镜头上的点(u,v)在光圈之外,它的值为0,否则为1。角度θ是在传感器表面测量的入射角;第四次功率来自变量的变化。当一个传感器像素对应于场景中的一个聚焦点时,辐照度来自于在场景中离开该点的亮度(位于场景中的聚焦平面上)。假设辐射LF在像素上是恒定的,在这种情况下,聚焦像素上的辐照度EF降低到
这里A(u,v)是一个“光圈”函数,可以模拟相机光圈:如果镜头上的点(u,v)在光圈之外,它的值为0,否则为1。角度θ是在传感器表面测量的入射角;第四次功率来自变量的变化。当一个传感器像素对应于场景中的一个聚焦点时,辐照度来自于在场景中离开该点的亮度(位于场景中的聚焦平面上)。假设辐射LF在像素上是恒定的,在这种情况下,聚焦像素上的辐照度EF降低到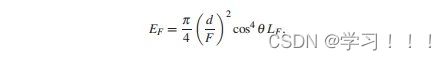 其中d是相机光圈的直径。值LF被称为像素的场景亮度。
其中d是相机光圈的直径。值LF被称为像素的场景亮度。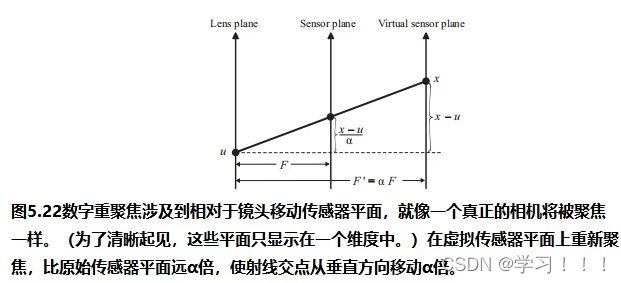 余弦因子有时被吸收到LF中,或者,在一个表面上很小的视场的情况下,被视为常数,然后从积分中分解出来。孔径函数同样可以被吸收到LF中,在这种情况下,方程(5.6)简化为仅
余弦因子有时被吸收到LF中,或者,在一个表面上很小的视场的情况下,被视为常数,然后从积分中分解出来。孔径函数同样可以被吸收到LF中,在这种情况下,方程(5.6)简化为仅 因此,EF与LF成正比。
因此,EF与LF成正比。
现在假设相机的焦距改变了,这相当于改变了镜头与传感器平面之间的距离F,如图5.22所示。传感器平面的新位置,在图5.22中称为“virtual sensor plane”,放置在距离为F'= αF。在F'的传感器平面上的新光场LF'成为原始传感器平面光场的“剪切”版本: 然后,通过将公式(5.8)代入公式(5.7),给出光位点辐照度(像素值):
然后,通过将公式(5.8)代入公式(5.7),给出光位点辐照度(像素值): 因此,数字重聚焦是一个评估这个积分的问题,给定了相机内光场LF。
因此,数字重聚焦是一个评估这个积分的问题,给定了相机内光场LF。
使用多光照相机进行的光场摄影。为了捕捉相机内光场,Ng等构建了一个设备,他们称之为“光场相机”基于相机提出“单镜头立体相机”发表于1992年由Adelson and Wang [Adelson and Wang 92]. 一个普通相机从遥远的聚焦平面聚焦光,使这个平面的光线汇聚在传感器阵列(或胶片平面)的相应点上。假设将阵列针孔放置在传感器阵列的前面,图像聚焦在这个表面上。每个针孔以盘状图像的形式将收敛的光扩散到传感器平面上,这代表了通过针孔可以看到的东西。然后,传感器平面图像将这些图像记录成一个图像,看起来像一组场景的小图像,每个图像都从一个稍微不同的视角捕获。明智地放置针孔表面,使这些图像的大小最大化,这样它们就可以相互接触。
Ng和他的合作者所描述的光场相机使用了这一原理,除了使用了一组微透镜来代替针孔表面。在光场相机中,图像聚焦在微透镜阵列上,每个微透镜创建一个通过传感器阵列上的镜头看到的小清晰图像。这幅图像被称为“微透镜图像”,它由一组与微透镜相对应的像素记录下来。因此,光场相机捕捉到的图像似乎是一组物体的小图像,每个图像的视场比原始像素组对应的视场大几倍(图5.23)。 每张微图像包含一个小的相机内光场切片。针孔模型有助于说明原因。微透镜阵列放置在传感器阵列的位置,因此(x,y)参数对应于微透镜表面点。考虑以at(xm,ym)为中心的微透镜。对应微透镜图像上的点传感器像素(u',v')记录了连接像素中心和微透镜中心的线的辐射。因此,参数(u',v')对应于透镜参数(u、v),因此微透镜图像记录了LF的样本(xm、ym、u、v)。因此,每张微图像中的像素数对应于定向采样密度;微透镜的数量,与位置采样密度有关。作者描述的原型有一个296×296微透镜阵列,每个微透镜对应一个大约13像素宽的微图像(透镜和像素之间的对应不需要精确)。数字重聚焦可以应用使用公式(5.9)与LF插值和重采样适当。
每张微图像包含一个小的相机内光场切片。针孔模型有助于说明原因。微透镜阵列放置在传感器阵列的位置,因此(x,y)参数对应于微透镜表面点。考虑以at(xm,ym)为中心的微透镜。对应微透镜图像上的点传感器像素(u',v')记录了连接像素中心和微透镜中心的线的辐射。因此,参数(u',v')对应于透镜参数(u、v),因此微透镜图像记录了LF的样本(xm、ym、u、v)。因此,每张微图像中的像素数对应于定向采样密度;微透镜的数量,与位置采样密度有关。作者描述的原型有一个296×296微透镜阵列,每个微透镜对应一个大约13像素宽的微图像(透镜和像素之间的对应不需要精确)。数字重聚焦可以应用使用公式(5.9)与LF插值和重采样适当。
然而,有一种更好的方法来执行数字重新聚焦,采用对光场相机图像的替代解释。微图像中的一个像素对应于一个小光锥,可以看作是来自镜头上的一个小虚拟光圈——就像镜头上的针孔。根据投影的本质,每个微图像中相应的像素从几乎相同的虚拟光圈获得光。将所有这些像素(每个微透镜都有一个像素)收集到一个单独的图像中,将生成一个子光圈图像(图5.24)。每个微图像像素都有一个子光圈图像,每个子图像都从略微不同的角度显示物体。由于有效孔径很小,每个子孔径图像都显得清晰,即基本上具有无限的景深。这种锐化能力是光场相机的一个重要特征,尽管亚光圈图像只有微透镜阵列的分辨率。碰巧,式(5.9)被积函中的LF值只是子光圈图像的缩放和移放版本,所以重新聚焦等于对整个镜头上移放和缩放的子光圈图像求和。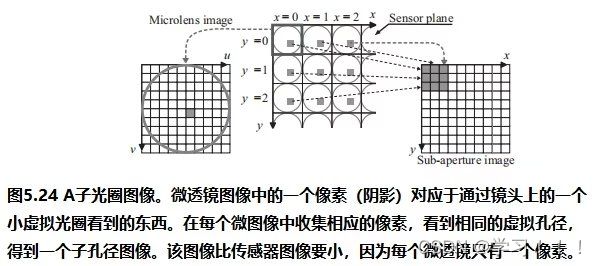 “Light Field Camera” 论文介绍了捕获和重聚焦技术的实验验证,并验证了再聚焦性能的有效性这取决于光场的采样率。特别是重新聚焦的锐度和可能的重新聚焦深度的范围与方向分辨率成线性正比。然而,该方法依赖于一些近似假设,由于缺乏参考解决方案,使得很难量化光场的精度和渲染图像的误差。
“Light Field Camera” 论文介绍了捕获和重聚焦技术的实验验证,并验证了再聚焦性能的有效性这取决于光场的采样率。特别是重新聚焦的锐度和可能的重新聚焦深度的范围与方向分辨率成线性正比。然而,该方法依赖于一些近似假设,由于缺乏参考解决方案,使得很难量化光场的精度和渲染图像的误差。
Fourier slice photography(傅里叶切片摄影)。Ng在论文“Fourier slice photography”中提出了一个光场的数学框架,为光场成像提供了理论基础[Ng 05]。本文的主要结果是一个被称为傅里叶切片摄影定理,它提供了一种从傅里叶域的光场创建图像的方法。该定理是基于一个已知定理的推广,即涉及两种函数降维的傅里叶切片定理。为了更精确地说,假设F是n个实变量的实值函数。通过积分F的一些变量,得到了对F的积分投影,得到了m个变量的函数。例如,公式(5.7)中确定传感器像素处的辐照度的积分是一个积分投影:
 (这是cos4 θ因子和孔径函数被省略或吸收到LF中的原因之一)。切片是通过固定多元函数的一些变量而得到的另一种降维方法。函数切片的一个例子是微透镜在(xm、ym)处的图像的辐射分布LF (xm、ym、u、v)。傅立叶切片定理指出,函数积分变换的傅立叶变换是函数傅立叶变换的切片。与涉及多次积分的积分投影相比,切片的计算几乎微不足道——傅立叶切片定理的好处就在于此。
(这是cos4 θ因子和孔径函数被省略或吸收到LF中的原因之一)。切片是通过固定多元函数的一些变量而得到的另一种降维方法。函数切片的一个例子是微透镜在(xm、ym)处的图像的辐射分布LF (xm、ym、u、v)。傅立叶切片定理指出,函数积分变换的傅立叶变换是函数傅立叶变换的切片。与涉及多次积分的积分投影相比,切片的计算几乎微不足道——傅立叶切片定理的好处就在于此。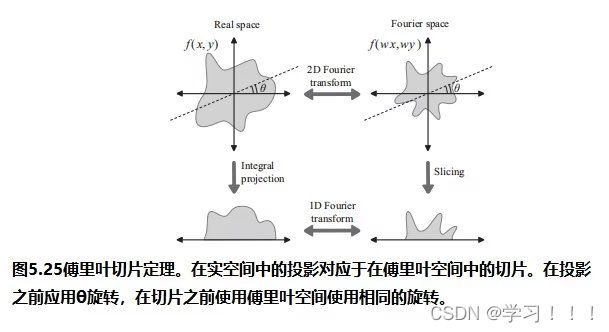 积分投影和切片可以推广到包括变量的线性变换,这也被称为基的变化。这并不影响傅里叶切片定理的有效性,因为傅里叶变换本身是线性的,这意味着它“通过”线性变换。图5.25说明了在这个更一般的背景下的傅里叶切片定理:投影和切片都在坐标旋转θ后应用。方程(5.9)中隐含的重聚焦变换实际上是光场参数的线性变换:
积分投影和切片可以推广到包括变量的线性变换,这也被称为基的变化。这并不影响傅里叶切片定理的有效性,因为傅里叶变换本身是线性的,这意味着它“通过”线性变换。图5.25说明了在这个更一般的背景下的傅里叶切片定理:投影和切片都在坐标旋转θ后应用。方程(5.9)中隐含的重聚焦变换实际上是光场参数的线性变换: 因此,从相机内光场重新聚焦图像的过程可以表示为经过参数的线性变换(方程(5.11))后的光场的积分投影(方程(5.10))。根据傅里叶切片定理,重聚焦图像的傅里叶变换是相机内光场的四维傅里叶变换的二维切片。这一点,结合所涉及的特定变换,就是傅里叶切片摄影定理。
因此,从相机内光场重新聚焦图像的过程可以表示为经过参数的线性变换(方程(5.11))后的光场的积分投影(方程(5.10))。根据傅里叶切片定理,重聚焦图像的傅里叶变换是相机内光场的四维傅里叶变换的二维切片。这一点,结合所涉及的特定变换,就是傅里叶切片摄影定理。
在傅里叶域中,采样和图像质量的分析在数学上更简单。“Fourier Slice Photography”该论文的数学框架允许对“Light Field Photography
”论文中的一些实验结果进行理论证明。特别地,它对精确重聚焦的可用范围设置了限制,并证明了锐度随方向采样率的线性增加。分析还表明,“数字重新聚焦的照片是精确照片的2D(低通)过滤版本”,这为重新聚焦的照片的噪音提供了证据。总之,本文回答了获得光场的重聚焦图像质量的问题。
傅里叶切片摄影定理导致了一种更有效的数字重聚焦算法(在更快和更少依赖于光场的采样率的意义上),称为傅里叶切片数字重聚焦。如图5.26所示,首先计算一个四维光场的傅里叶变换,然后在傅里叶域内进行重新聚焦的操作(剪切和二维切片的应用)。结果的逆变换是最终的图像。这种方法的另一个特点是,四维光场的傅里叶变换,这是最昂贵的部分,只需要根据需要对许多不同的重新聚焦计算一次。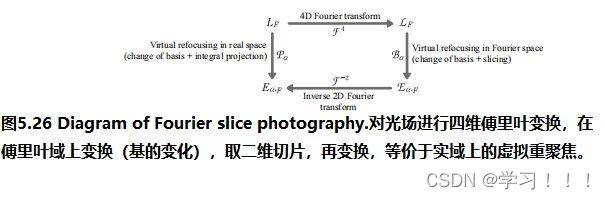 图5.27包含了使用傅里叶变换的数字重聚焦过程的图像。第一行显示由光场相机捕获的光场。特写镜头包括在右边。第二行显示了光场的傅里叶变换,排列成一个二维图像,类似于光场在二维光场图像中的存储方式。第三行包含四维变换数据的切片,在对三种重聚焦排列分别应用剪切变换后;从左到右,α > 1,α = 1,α < 1。(注意,傅里叶变换图像与实际图像不是很好,尽管它们看起来很有趣。)最下面的两行显示了重新聚焦的图像。第二最低行的图像是上面图像中所示的二维傅里叶变换切片的逆变换。在底部的图片由方程(5.9)的直接积分呈现,并提供以供比较。
图5.27包含了使用傅里叶变换的数字重聚焦过程的图像。第一行显示由光场相机捕获的光场。特写镜头包括在右边。第二行显示了光场的傅里叶变换,排列成一个二维图像,类似于光场在二维光场图像中的存储方式。第三行包含四维变换数据的切片,在对三种重聚焦排列分别应用剪切变换后;从左到右,α > 1,α = 1,α < 1。(注意,傅里叶变换图像与实际图像不是很好,尽管它们看起来很有趣。)最下面的两行显示了重新聚焦的图像。第二最低行的图像是上面图像中所示的二维傅里叶变换切片的逆变换。在底部的图片由方程(5.9)的直接积分呈现,并提供以供比较。 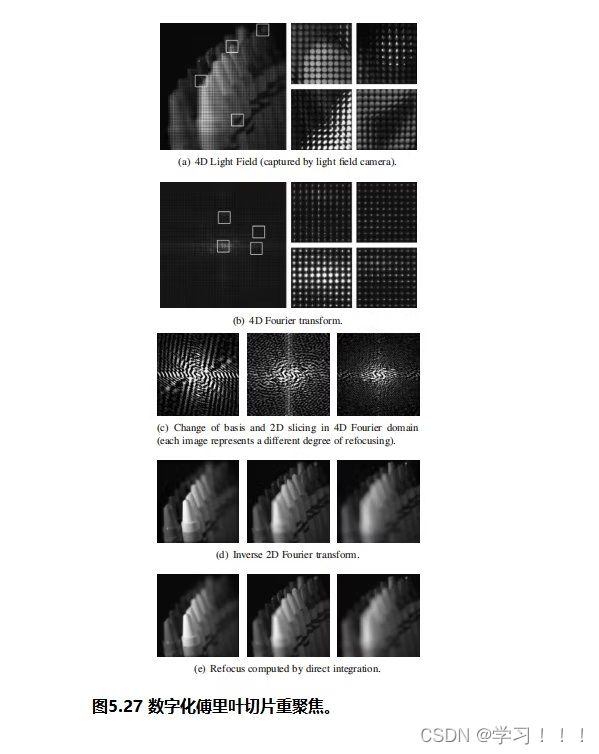
可以肯定地说,Ng等人的光场摄影工作和Ng的傅立叶切片摄影论文为光场的一系列新应用打开了大门,并重振了该领域的研究。事实上,这些论文是在计算摄影这一新的研究领域开始起步的时候发表的。最初的基于图像的技术的目标是从传统相机所需的照片中恢复真实世界的外观。计算摄影涉及开发新设备,以最适合特定目的的方式捕捉和记录摄影数据。吴的两篇论文极大地启发了这一领域的重新探索。在计算摄影中出现了各种试图扩展相机内光场可能性的实用方法[Georgeiv et al.06][Veeraraghavan et al.07][Raskar et al.08][Liang et al.08][Lanman et al.08][Hirsch et al.09]。可以说,计算摄影的出现将光场带入了一个新的实用时代。
Refrenece:
[E. Kruppa] Translation of “Zur Ermittlung eines Objektes aus zwei Perspektivenmit innerer Orientierung” by Erwin Kruppa (1913)∗.
[Beauchemin and Barron 95] S. S. Beauchemin and J. L. Barron. “The Computation of Optical Flow.” ACM Comput. Surv. 27:3 (1995), 433–466.
[Sand and Teller 04] Peter Sand and Seth Teller. “Video Matching.” Proc. SIGGRAPH’04, Transactions on Graphics 23:3 (2004), 592–599.
[Debevec et al. 96] Paul E. Debevec, Camillo J. Taylor, and Jitendra Malik. “Modeling and Rendering Architecture from Photographs.” Technical
Report CSD-96-893, University of California at Berkeley,1996.
[Wachowski and Wachowski 99] Andy Wachowski and Larry Wachowski. The Matrix.VFX: Manex Visual Effects et al. 1999.
[Gondry 95] Michel Gondry. “Like A Rolling Stone.” VFX: BUF. 1995.
[Levoy and Hanrahan 96] Marc Levoy and Pat Hanrahan. “Light Field Rendering.” In Proceedings of SIGGRAPH ’96: Computer Graphics Proceedings, Annual Conference Series, edited by Holly Rushmeier, pp. 31–42. Reading, MA: AddisonWesley,1996.
[Gortler et al. 96] Steven J. Gortler, Radek Grzeszczuk, Richard Szeliski, and Michael F.Cohen. “The lumigraph.” In Proceedings of SIGGRAPH 96, Computer Graphics Proceedings, Annual Conference Series, edited by Holly Rushmeier, pp. 43–54,Reading, MA: Addison-Wesley, 1996.
[Raskar and Tumbin 09] Ramesh Raskar and Jack Tumbin. Computational Photography:Mastering New Techniques for Lenses, Lighting, and Sensors. Natick, MA: A K Peters Ltd., 2009.
[Chen et al. 02] Wei-Chao Chen, Jean-Yves Bouguet, Michael H. Chu, and RadekGrzeszczuk. “Light Field Mapping: Efficient Representation and Hardware Rendering of Surface Light Fields.” Proc. SIGGRAPH ’02, Transactions on Graphics 21:3 (2002), 447–456.
[Fournier 95] Alan Fournier. “Separating Reflectance Functions for Linear Radiosity.” In Rendering Techniques ’95: Proceedings of the Eurographics Workshop in Dublin,Ireland, June 12–14, 1995, edited by P. Hanrahan and W. Purgathofer, pp 296–305.Wien: Springer-Verlag, 1995.
[Ng 05] Ren Ng. “Fourier Slice Photography.” Proc. SIGGRAPH ’05, Transactions on Graphics 24:3 (2005), 735–744.
[Georgeiv et al. 06] T. Georgeiv, K.C. Zheng, B. Curless, D. Salesin, S. Nayar, and C. Intwala. “Spatio-angular Resolution Tradeoff in Integral Photography.” In Rendering Techniques 2006: Eurographics Symposium on Rendering, Nicosta, Cyprus, June 26–29, 2006, edited by Tomas Akenine-M¨oller and Wolfgang Heidrich, pp. 263–272. Aire-La-Ville, Switzerland: Eurographics Association, 2006
[Veeraraghavan et al. 07] Ashok Veeraraghavan, Ramesh Raskar, Amit Agrawal, Ankit Mohan, and Jack Tumblin. “Dappled Photography: Mask Enhanced Cameras for Heterodyned Light Fields and Coded Aperture Refocusing.” Proc. SIGGRAPH ’07,Transactions on Graphics 26:3 (2007), 69.
[Adelson and Wang 92] Edward H. Adelson and John Y. A. Wang. “Single Lens Stereo with a Plenoptic Camera.” IEEE Trans. Pattern Anal. Mach. Intell. 14:2 (1992), 99–106.
[Ng 05] Ren Ng. “Fourier Slice Photography.” Proc. SIGGRAPH ’05, Transactions on Graphics 24:3 (2005), 735–744.
[Raskar et al. 08] Ramesh Raskar, Amit Agrawal, Cyrus A. Wilson, and Ashok Veeraraghavan. “Glare Aware Photography: 4D Ray Sampling for Reducing Glare Effects of Camera Lenses.” Proc. SIGGRAPH ’08, Transactions on Graphics 27:3 (2008), 1–10.
[Liang et al. 08] Chia-Kai Liang, Tai-Hsu Lin, Bing-Yi Wong, Chi Liu, and Homer H. Chen. “Programmable Aperture Photography: Multiplexed Light Field Acquisition.”Proc. SIGGRAPH ’08, Transactions on Graphics 27:3 (2008), 1–10.
[Hirsch et al. 09] Matthew Hirsch, Douglas Lanman, Henry Holtzman, and Ramesh Raskar. “BiDi Screen: A Thin, Depth-Sensing LCD for 3D Interaction Using Light Fields.” Proc. SIGGRAPH Asia ’09, Transactions on Graphics 28:5 (2009), 1–9.