算法——哈希表
哈希表简介
**是什么:**存储数据的容器
有什么用:快速查找某个元素,时间复杂度O(1),空间复杂度O(n)
**什么时候使用哈希表:**频繁查找某一个数(这里不要忘了之前的二分,时间复杂度O(logN))
怎么用哈希表: 1.容器 2.用数组模拟简易哈希表
两数之和
两数之和
题目解析
- 该数组中找出 **和为目标值 **target 的那 两个 整数,并返回它们的数组下标。
- 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
- 按任意顺序返回答案
算法原理
解法一:暴力解法
之前的枚举是,固定一个指针,向后移动另一个指针开始遍历,直到找到目标值。这次枚举我们依然先固定一个指针,然后遍历这个数之前的数字,遍历完仍然向后移动另一个指针。时间复杂度O(n2)
解法二:使用哈希表优化
暴力解法遍历指针之前的数字所消耗的时间复杂度是O(n),如果我们将所要遍历的数字放到哈希表里,那我们的就只需要花费O(1)的时间复杂度就能够找到。总体时间复杂度消耗为O(n),空间复杂度也为O(n);典型的空间换时间。在哈希表里存储的是数字和下标一起绑定存储
为什么之前的遍历不好用呢?
把数组全放入哈希表中时,如果我们所要找的数和自身相等时,那就会找到自身,这是不符合题意的。这种情况是需要特判的。但我们运用上面的的哈希表做优化就不会遇到这种边界问题。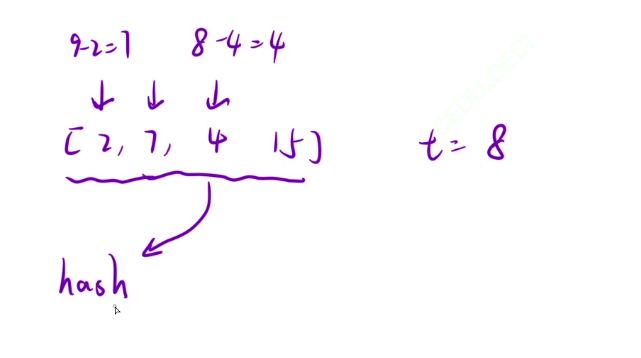
代码实现
class Solution
{
public:
vector<int> twoSum(vector<int>& nums, int target)
{
unordered_map<int, int> hash; // 判定是否为字符重排
判断是否为字符重排
题目解析
给定两个由小写字母组成的字符串 s1 和 s2
其中一个字符串的字符重新排列后,能否变成另一个字符串。
算法原理
解法一:模拟:将字符串所有组成可能性全部列出来,然后进行比较。但是时间复杂度是指数级别的,非常恐怖
解法二:哈希表: 如果s1能够重排s2,那么每个字符出现的次数肯定相同。那么我们可以使用哈希表,但是我们是使用容器还是使用数组模拟呢。如果使用容器,要找hash1里字符的int和hash2里对应字符的int进行比较,较为麻烦。因为题目中说了只由小写字母组成,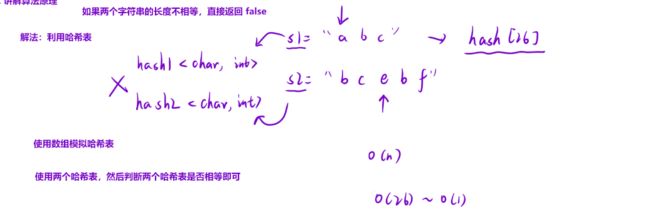
**优化:只使用一个哈希表:**只用一个哈希表记录s1字符出现的次数,然后遍历s2,s2中出现的字符在hash1中减掉1即可。当两个字符串的⻓度不相等的时候,是不可能构成互相重排的,直接返回false
代码实现
class Solution
{
public:
bool CheckPermutation(string s1, string s2)
{
if(s1.size() != s2.size()) return false;
int hash[26] = { 0 };
// 先统计第⼀个字符串的信息
for(auto ch : s1)
hash[ch - 'a']++;
// 扫描第⼆个字符串,看看是否能重排
for(auto ch : s2)
{
//a映射到字符下标为0,所以-‘a’
hash[ch - 'a']--;
if(hash[ch - 'a'] < 0) return false;
}
return true;
}
};
存在重复元素I
存在重复元素I
题目解析
如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
算法原理
和两数之和相同,固定一个数,找在他之前的数有没有出现重复。这里我们的hash表只需要存一个k值就行
代码实现
class Solution
{
public:
bool containsDuplicate(vector<int>& nums)
{
unordered_set<int> hash;
for(auto x : nums)
if(hash.count(x)) return true;
else hash.insert(x);
return false;
}
};
存在重复元素II
存在重复元素II
题目解析
判断数组中是否存在两个 不同的索引_ i 和 _j ,满足 nums[i] == nums[j] 且 abs(i - j) <= k
算法原理
解法:哈希表
表里存储字符和下标,将数组中的数字和其对应的下标一起绑定存入hash表中。开始移动。当发现前面由相同元素时,将两个下标相减,发现不符合条件,将1(紫色指针所指的)放入hash表中,此时存入的<1,3>就把最开始的<1,0>覆盖掉了。继续向后移动。当移动到下一个1时,只需要考虑里第三个1最近位置的1(即第二个1)即可。因为如果最远位置的符合条件(第一个1),那么近的位置也符合。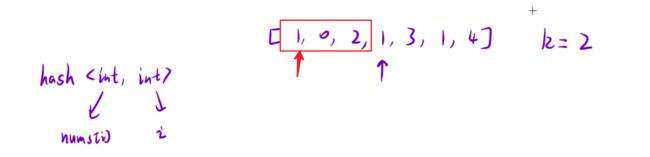
思考题:如果数组内存在⼤量的「重复元素」,⽽我们判断下标所对应的元素是否符合条件的时候,需要将不同下标的元素作⽐较,怎么处理这个情况呢?
答:这⾥运⽤了⼀个「⼩贪⼼」。我们按照下标「从⼩到⼤」的顺序遍历数组,当遇到两个元素相同,并且⽐较它们的下标时,这两个下标⼀定是距离最近的,因为:
• 如果当前判断符合条件直接返回 true ,⽆需继续往后查找。
• 如果不符合条件,那么前⼀个下标⼀定不可能与后续相同元素的下标匹配(因为下标在逐渐变⼤),那么我们可以⼤胆舍去前⼀个存储的下标,转⽽将其换成新的下标,继续匹配
代码实现
class Solution
{
public:
bool containsNearbyDuplicate(vector<int>& nums, int k)
{
unordered_map<int, int> hash;
for(int i = 0; i < nums.size(); i++)
{
if(hash.count(nums[i]))
{
if(i - hash[nums[i]] <= k) return true;
}
hash[nums[i]] = i;
}
return false;
}
};
字母异位词分组
字母异位词分组
题目解析
算法原理
解法:哈希表
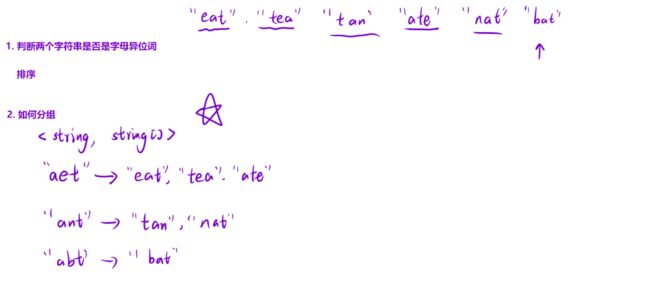
- 判断两个字符串是否为字母异位词:我们可以用哈希表判断,这里我们使用排序,虽然这样时间复杂度更高,但是代码好写一些。按照ASCII码值排序
- 如何分组:借助容器,我们将k值定位为string,Value值定义为字符串数组string(K-V)。遍历第一个字符串eat,按照ASCII码值排序之后为aet,这里作为k值的string,然后将原始数组中的字符串开始作为V值遍历比较。将eat排完序后发现hash表里由aet,存入,然后继续向后遍历。若发现排序完之后没有,创建一个新的(如ant)再继续比较
代码实现
class Solution
{
public:
vector<vector<string>> groupAnagrams(vector<string>& strs)
{
unordered_map<string, vector<string>> hash;
// 1. 把所有的字⺟异位词分组
for(auto& s : strs)
{
string tmp = s;
sort(tmp.begin(), tmp.end());
hash[tmp].push_back(s);
}
// 2. 结果提取出来
vector<vector<string>> ret;
for(auto& [x, y] : hash)
{
ret.push_back(y);
}
return ret;
}
};
