微积分-第二章三角函数(合集)
第二章三角函数
在处理微积分问题时,我们不可避免的会遇到三角函数。学会三角函数对于微积分是非常重要的。
2.1基本知识
学习三角函数我们需要先学习一些基本知识。
首先要学习的是弧度的概念。弧度是一种角的度量单位,用于测量角的大小。它是根据角所对的弧长与该弧所在圆的半径之比来定义的。
单位为1的单位圆的圆心角的弧度就是 2 π 2\pi 2π。因为圆的周长公式是 2 π r 2\pi r 2πr,而单位圆的半径为1,所以圆心角的弧度是 2 π 2 \pi 2π。
![]()
弧度和角度之间可以相互转换,有公式
弧度 = 角度 × π 180 弧度 = 角度 \times \frac{\pi}{180} 弧度=角度×180π
角度 = 弧度 × 180 π 角度 = 弧度 \times \frac{180}{\pi} 角度=弧度×π180
下表是我们常用的角度和弧度的转换
| 角度 | 弧度 |
|---|---|
| 0° | 0 |
| 30° | π 6 \frac{\pi}{6} 6π |
| 45° | π 4 \frac{\pi}{4} 4π |
| 60° | π 3 \frac{\pi}{3} 3π |
| 90° | π 2 \frac{\pi}{2} 2π |
| 180° | π \pi π |
| 270° | 3 π 2 \frac{3\pi}{2} 23π |
| 360° | 2 π 2\pi 2π |
我们扩展了角的度量单位,现在来让我们从三角型中来学习三角函数。
知道如何从三角形中定义三角函数是非常重要的。让我们从直角三角形开始。
![]()
我们记除直角外的一角为θ,则三角函数的公式为
s i n ( θ ) = 对边 斜边 , c o s ( θ ) = 邻边 斜边 , t a n ( θ ) = 对边 邻边 sin(\theta)=\frac{对边}{斜边} ,cos(\theta)=\frac{邻边}{斜边},tan(\theta)=\frac{对边}{邻边} sin(θ)=斜边对边,cos(θ)=斜边邻边,tan(θ)=邻边对边
这三个是最常用的三角函数。有时我们也会用到其他三个函数,它们被定义为:
s e c ( θ ) = 1 c o s ( θ ) , c s c ( θ ) = 1 s i n ( θ ) , c o t ( θ ) = 1 t a n ( θ ) sec(\theta)=\frac{1}{cos(\theta)},csc(\theta)=\frac{1}{sin(\theta)},cot(\theta)=\frac{1}{tan(\theta)} sec(θ)=cos(θ)1,csc(θ)=sin(θ)1,cot(θ)=tan(θ)1
记住下表中的内容是很有必要的
| 0 | π 6 \frac{\pi}{6} 6π | π 4 \frac{\pi}{4} 4π | π 3 \frac{\pi}{3} 3π | π 2 \frac{\pi}{2} 2π | |
|---|---|---|---|---|---|
| sin | 0 | 1 2 \frac{1}{2} 21 | 1 2 \frac{1}{\sqrt{2}} 21 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 |
| cos | 1 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 2 \frac{1}{\sqrt{2}} 21 | 1 2 \frac{1}{2} 21 | 0 |
| tan | 0 | 1 3 \frac{1}{\sqrt{3}} 31 | 1 | 3 \sqrt{3} 3 | 无定义 |
虽然数学不是死记硬背,但是有些内容还是非常值得记忆的。
2.2 扩展三角函数
在上一节中,讨论了如何在直角三角形中定义三角函数,限制让我们扩展三角函数的定义域。
事实上我们可以取任意角的正弦和余弦,而不只是局限于 0 0 0~ π 2 \frac{\pi}{2} 2π当中。
当然需要注意的是,正切函数对不是对任意角都成立。如 t a n ( π 2 ) tan(\frac{\pi}{2}) tan(2π)就是无定义的。
我们先从 0 0 0~ 2 π 2\pi 2π之间的角开始。我们需要从坐标平面中来定义三角函数。
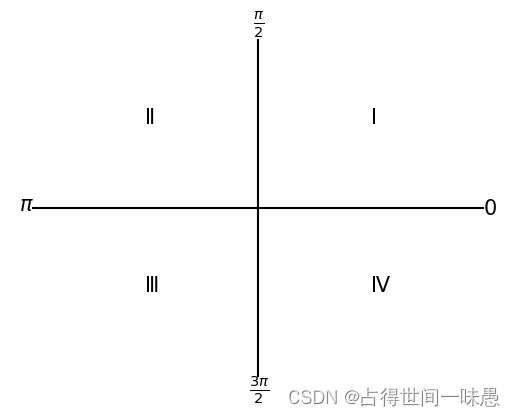
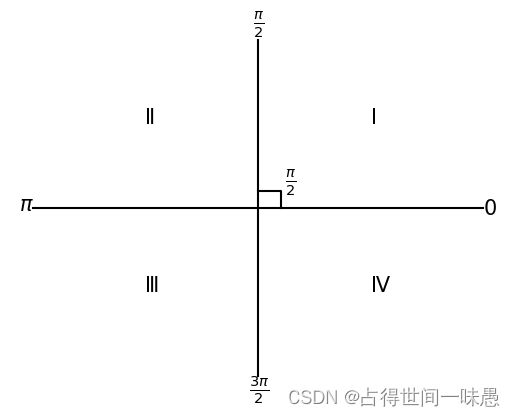
坐标轴将坐标平面分成了四个象限。分别称为第一象限、第二象限、第三象限、第四象限。我们可以看到象限标记的走向是逆时针。大家可能已经注意到了坐标轴上的数字了。我想大家已经猜出它们是什么了。它们表示的是标记表示的从原点出发射线与x正半轴的夹角的弧度。或者说是从原点出发射线在x轴正半轴逆时针转动的弧度。
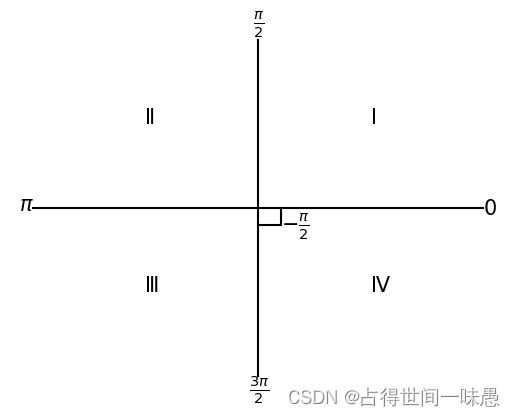
如果顺时针转动则弧度是负的
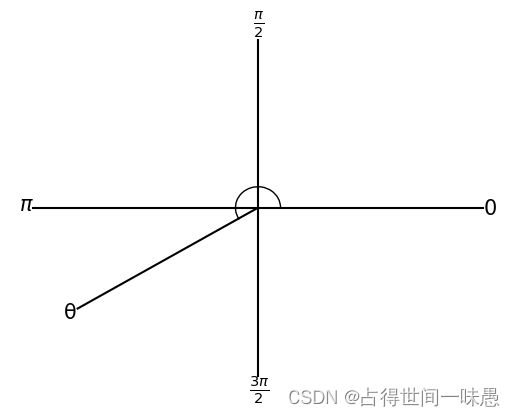
让我们取某个角 θ \theta θ,并在坐标平面中画出来
这里要注意,这里是将射线标记为θ,而不是角本身。我们在射线θ上选取一点$(x,y)并从该点画一条垂线至x。
图片中标记出了三个量。该点的x坐标和y坐标,以及该点到原点的距离r。有了这三个点我们便可以定义如下的三角函数:
s i n ( θ ) = y r , c o s ( θ ) = x r , t a n ( θ ) = y x sin(\theta)=\frac{y}{r},cos(\theta)=\frac{x}{r},tan(\theta)=\frac{y}{x} sin(θ)=ry,cos(θ)=rx,tan(θ)=xy
这与上一节的公式是一样的。上图中我们构造了一个直角三角形,其中x、y、r分别是邻边、对比、斜边。
为了方便计算,我们常常假设 r = 1 r=1 r=1。这样得到的点 ( x , y ) (x,y) (x,y)就会落在单位圆上。上述的公式也可以简化为
s i n ( θ ) = y , c o s ( θ ) = x , t a n ( θ ) = y x sin(\theta)=y,cos(\theta)=x,tan(\theta)=\frac{y}{x} sin(θ)=y,cos(θ)=x,tan(θ)=xy
我们怎么求解三角函数呢?让我们来看一个具体的例子,求 s i n ( 4 π 3 ) sin(\frac{4\pi}{3}) sin(34π)。让我们画出它的图像。
我们知道 s i n ( θ ) = y sin(\theta)=y sin(θ)=y,所以求 s i n ( 4 π 3 ) sin(\frac{4\pi}{3}) sin(34π)就需要求出 y y y多少。让我们把目光放在图像中构造出来三角形中。 y y y的绝对值就是这个三角形θ角的对边的长度。上一节中我们说过 s i n ( θ ) = 对边 斜边 sin(\theta)=\frac{对边}{斜边} sin(θ)=斜边对边,我们已经假设了 r = 1 r=1 r=1。所以 ∣ y ∣ = s i n ( α ) |y|=sin(\alpha) ∣y∣=sin(α)。
α \alpha α是角 4 π 3 \frac{4\pi}{3} 34π的射线与x轴负半轴的夹角。所以我们有 α = π − 4 π 3 = π 3 \alpha=\pi - \frac{4\pi}{3}=\frac{\pi}{3} α=π−34π=3π。
我们有 ∣ s i n ( 4 π 3 ) ∣ = s i n ( π 3 ) = 3 2 |sin(\frac{4\pi}{3})|=sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2} ∣sin(34π)∣=sin(3π)=23。
我们怎么确定它的符号呢?很简单看象限就可以了。角 4 π 3 \frac{4\pi}{3} 34π在第三象限,所以 y < 0 y<0 y<0。最终我们可以得到 s i n ( 4 π 3 ) = − s i n ( π 3 ) = − 3 2 sin(\frac{4\pi}{3})=-sin(\frac{\pi}{3})=-\frac{\sqrt{3}}{2} sin(34π)=−sin(3π)=−23
这个小角称为参考角,一般来说参考角是角 θ \theta θ的射线与x轴之间最小的角。它介于0~ 2 π 2\pi 2π之间。角 θ \theta θ的三角函数的绝对值与参考角的三角函数值一致。角 θ \theta θ的三角函数值的符号取决于它射线所在的象限。
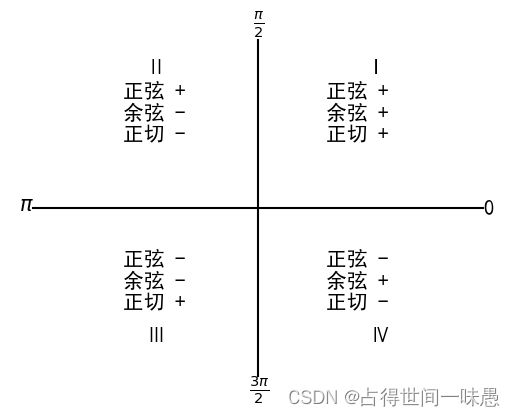
在第一象限中,x和y都是正的。所以射线位于第一象限中的任意角的正弦、余弦和正切都必定为正。
在第二象限中,x为负,y为正。所以射线位于第二象限的任意角的正弦为正;余弦和正切为负
第三象限中,x和y都为负。所以射线位于第三象限的任意角的正弦和余弦都为负;正切为正。
在第四象限中,x为正,y为负。所以射线位于第四象限的任意角的余弦为正;正弦和正切为负
为了方便大家记忆,我这里为大家总结为以下内容:第一象限全为正,第二象限sin为为正、第三象限tan为正、第四象限cos为正。其余全为负。
现在让我们做几个练习题。
求角 5 π 4 \frac{5\pi}{4} 45π的正弦、余弦和正切。
首先我们需要判断这个角的射线在第几象限,确认三角函数值的符号和参考角。因为 π ≤ 5 π 4 ≤ 3 π 2 \pi \leq \frac{5\pi}{4} \leq \frac{3\pi}{2} π≤45π≤23π,所以射线位于第三象限。第二步求出它的参考角 α \alpha α: α = 5 π 4 − π = π 4 \alpha=\frac{5\pi}{4}-\pi=\frac{\pi}{4} α=45π−π=4π。第三步求出参考角的三角函数: s i n ( π 4 ) = 1 2 sin(\frac{\pi}{4})=\frac{1}{\sqrt{2}} sin(4π)=21。结合上图中的第三象限三角函数的符号最终我们可以得到:
s i n ( 5 π 4 ) = − s i n ( π 4 ) = − 1 2 c o s ( 5 π 4 ) = − c o s ( π 4 ) = − 1 2 t a n ( 5 π 4 ) = t a n ( π 4 ) = 1 sin(\frac{5\pi}{4})=-sin(\frac{\pi}{4})=-\frac{1}{\sqrt{2}}\\ cos(\frac{5\pi}{4})=-cos(\frac{\pi}{4})=-\frac{1}{\sqrt{2}}\\ tan(\frac{5\pi}{4})=tan(\frac{\pi}{4})=1 sin(45π)=−sin(4π)=−21cos(45π)=−cos(4π)=−21tan(45π)=tan(4π)=1
求角 2 π 3 \frac{2\pi}{3} 32π的正弦值。
因为 π 2 ≤ 2 π 3 ≤ π \frac{\pi}{2} \leq \frac{2\pi}{3} \leq \pi 2π≤32π≤π 。故角 2 π 3 \frac{2\pi}{3} 32π位于第二象限。它的参考角为: π − 2 π 3 = π 3 \pi - \frac{2\pi}{3} =\frac{\pi}{3} π−32π=3π。最终我们可以得到 s i n ( 2 π 3 ) = s i n ( π 3 ) = 3 2 sin(\frac{2\pi}{3})=sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2} sin(32π)=sin(3π)=23
我们来总结一下计算步骤
- 判断这个角的射线在第几象限
- 找出这个角的参考角
- 求参考角的三角函数值
- 根据角所在象限确认这个角的三角函数值的符号
考虑角 6 π 7 \frac{6\pi}{7} 76π,它的正弦值是多少?它位于第二象限,且它的参考角为 π 7 \frac{\pi}{7} 7π。所以 s i n ( 6 π 7 ) = s i n ( π 7 ) sin(\frac{6\pi}{7})=sin(\frac{\pi}{7}) sin(76π)=sin(7π)。这是不适应近似可以得到的最简形式。在求解微积分问题的时候,不建议取近似值。除非有明确要求。
0 ~ 2 π 2\pi 2π之外的角
现在让我们考虑 [ 0 , 2 π ] [0,2\pi] [0,2π]之外的角。在坐标平面中角的弧度就是从原点出发,射线从x轴正半轴开始,逆时针转动到某个位置,这个位置到x轴正半轴的夹角。夹角并不会止步于 2 π 2\pi 2π,每转动一圈弧度便会增加 2 π 2\pi 2π。因为转动一周是 2 π 2\pi 2π弧度。当弧度超过 2 π 2\pi 2π时,意味着射线已经绕原点转动了一周以上。而旋转 2 π 2\pi 2π弧度后射线会回到原来的位置。所以弧度加上 2 π 2\pi 2π的整数倍不会改变其在平面上的方向。
大于 2 π 2\pi 2π或小于 0 0 0的角与通过加上或减去 2 π 2\pi 2π的整数倍,最终得到位于 [ 0 , 2 π ] [0,2\pi] [0,2π]之间的角 α \alpha α是等价的。
考虑角 9 π 4 \frac{9\pi}{4} 49π的正弦值。我想大家已经看出来 9 π 4 > 2 π \frac{9\pi}{4}>2\pi 49π>2π。让我们对 9 π 4 \frac{9\pi}{4} 49π减去 2 π 2\pi 2π整数倍得到位于 [ 0 , 2 π ] [0,2\pi] [0,2π]的等价角 π 4 \frac{\pi}{4} 4π。所以 s i n ( 9 π 4 ) = s i n ( π 4 ) = 1 2 sin(\frac{9\pi}{4})=sin(\frac{\pi}{4})=\frac{1}{\sqrt{2}} sin(49π)=sin(4π)=21。
让我们来总结一下:
- sin ( θ + 2 k π ) = sin ( θ ) \sin(\theta+2k\pi)=\sin(\theta) sin(θ+2kπ)=sin(θ),其中 k ∈ N k \in N k∈N
- cos ( θ + 2 k π ) = cos θ ) \cos(\theta+2k\pi)=\cos\theta) cos(θ+2kπ)=cosθ),其中 k ∈ N k \in N k∈N
- tan ( θ + 2 k π ) = tan ( θ ) \tan(\theta+2k\pi)=\tan(\theta) tan(θ+2kπ)=tan(θ),其中 k ∈ N k \in N k∈N
2.3三角函数的图像
掌握三角函数的图像是非常有必要的。从上一节末尾我们可以直到三角函数是具有周期性的。这意味着它们的图像是从左到右的反复的重复自己。
考虑 sin ( x ) \sin(x) sin(x)的图像,画出它的图像很简单。我们先画出 [ 0 , 2 π ] [0,2\pi] [0,2π]上的图像。再“复制粘贴”就可以得到它的图像。
这里有四个关键点 ( 0 , 0 ) (0,0) (0,0)、 ( π 2 , 1 ) (\frac{\pi}{2},1) (2π,1)、 ( π , 0 ) (\pi,0) (π,0)、 ( 2 π , 0 ) (2\pi,0) (2π,0)。你应该记住这个图像。
sin ( x ) \sin(x) sin(x)是 x x x的周期函数,它的周期为 2 π 2\pi 2π。我们可以通过重复这个模式对图像进行扩展。
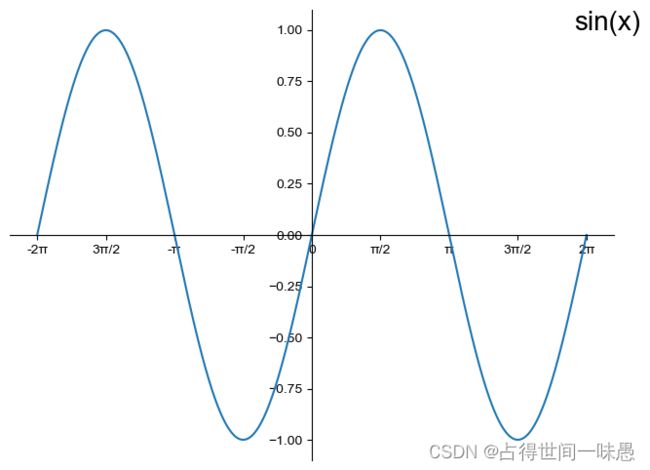
大家有没有从图中看出一个关键信息呢? sin ( x ) \sin(x) sin(x)关于原点对称,所以它是奇函数。
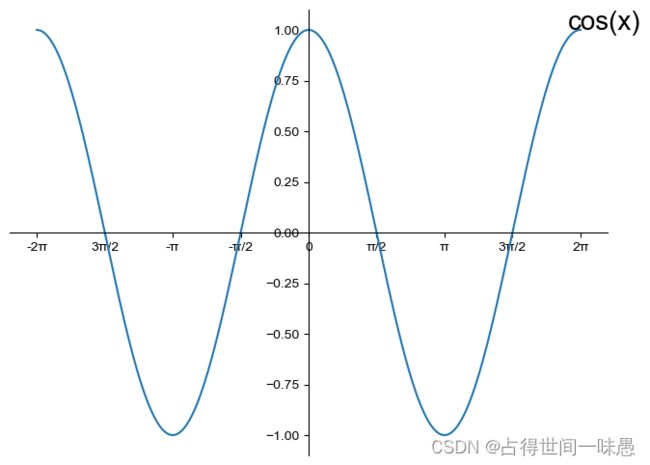
y = c o s ( x ) y=cos(x) y=cos(x)的图像与 y = s i n ( x ) y=sin(x) y=sin(x)的图像相似。 c o s ( x ) cos(x) cos(x)也是一个以 2 π 2\pi 2π为最小正周期的周期函数。
对图像进行扩展可以得到:
从图中可以看出 c o s ( x ) cos(x) cos(x)是一个关于y轴对称的偶函数。
t a n ( x ) tan(x) tan(x)与 s i n ( x ) sin(x) sin(x)和 c o s ( x ) cos(x) cos(x)不同,它的定义域不是全体实数。这是因为 t a n ( x ) = s i n ( x ) c o s ( x ) tan(x)=\frac{sin(x)}{cos(x)} tan(x)=cos(x)sin(x),它只有在 c o s ( x ) cos(x) cos(x)不为零时有定义。我们知道 c o s ( π 2 ) = 0 cos(\frac{\pi}{2})=0 cos(2π)=0, c o s ( π ) = 0 cos(\pi)=0 cos(π)=0。而函数 c o s ( x ) cos(x) cos(x)具有周期性。所以 c o s ( x + k π ) = 0 cos(x+k\pi)=0 cos(x+kπ)=0,其中 k ∈ N k \in N k∈N。最终我们有 x ≠ π 2 + k π x \neq \frac{\pi}{2}+k\pi x=2π+kπ,其中 k ∈ N k \in N k∈N。
画 t a n ( x ) tan(x) tan(x)时考虑到它存在垂直渐近线(无定义的点),所以最好是先画出 − π 2 -\frac{\pi}{2} −2π~ π 2 \frac{\pi}{2} 2π之间的点。

y = t a n ( x ) y=tan(x) y=tan(x)并不是以 2 π 2\pi 2π为周期,而是以 π \pi π为周期的周期函数。
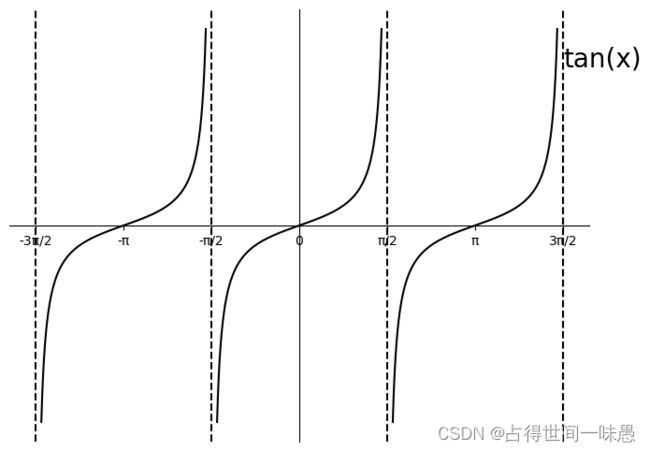
t a n ( x ) tan(x) tan(x)关于原点对称,是奇函数。
2.4三角恒等式
让我们来回顾一下三角函数
sin ( θ ) = y r , cos ( θ ) = x r , tan ( θ ) = y x sec ( θ ) = 1 cos ( θ ) , csc ( θ ) = 1 sin ( θ ) , cot = 1 tan ( θ ) \sin(\theta)=\frac{y}{r},\cos(\theta)=\frac{x}{r},\tan(\theta)=\frac{y}{x}\\ \sec(\theta)=\frac{1}{\cos(\theta)},\csc(\theta)=\frac{1}{\sin(\theta)},\cot=\frac{1}{\tan(\theta)} sin(θ)=ry,cos(θ)=rx,tan(θ)=xysec(θ)=cos(θ)1,csc(θ)=sin(θ)1,cot=tan(θ)1
经过变化我们可以得到:
tan ( θ ) = sin ( θ ) cos ( θ ) , cot = cos ( θ ) sin ( θ ) \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)},\cot=\frac{\cos(\theta)}{\sin(\theta)} tan(θ)=cos(θ)sin(θ),cot=sin(θ)cos(θ)
还记得如何用直角三角形中描述三角函数吗?在直角三角形中 x x x和 y y y是直角边, r r r是斜边。根据勾股定理(又称毕达哥拉斯定理)我们有 x 2 + y 2 = r 2 x^2+y^2=r^2 x2+y2=r2。通常我们假设 r = 1 r=1 r=1。所以我们有恒等式.
sin 2 ( θ ) + cos 2 ( θ ) = 1 \sin^2(\theta)+\cos^2(\theta)=1 sin2(θ)+cos2(θ)=1
对上式两边同时除以 cos ( θ ) 2 \cos(\theta)^2 cos(θ)2:
sin 2 ( θ ) cos 2 ( θ ) + cos 2 ( θ ) cos 2 ( θ ) = 1 c o s 2 ( θ ) \frac{\sin^2(\theta)}{\cos^2(\theta)}+\frac{\cos^2(\theta)}{\cos^2(\theta)}=\frac{1}{cos^2(\theta)} cos2(θ)sin2(θ)+cos2(θ)cos2(θ)=cos2(θ)1
可以得到
1 + tan 2 ( θ ) = s e c 2 ( θ ) 1+\tan^2(\theta)=sec^2(\theta) 1+tan2(θ)=sec2(θ)
对上式同时除以 s i n ( θ ) 2 sin(\theta)^2 sin(θ)2可以得到
1 + c o t 2 ( θ ) = c s c 2 ( θ ) 1+cot^2(\theta)=csc^2(\theta) 1+cot2(θ)=csc2(θ)
我们还有互补角公式。它们描述了在直角三角形中,一个角的正弦、正切和正割值与其互补角的余弦、余切和余割值之间的关系。具体来说:
s i n ( x ) = c o s ( π 2 − x ) 、 t a n ( x ) = c o t ( π 2 − x ) 、 s e c ( x ) = c s c ( π 2 − x ) sin(x)=cos(\frac{\pi}{2}-x)、tan(x)=cot(\frac{\pi}{2}-x)、sec(x)=csc(\frac{\pi}{2}-x) sin(x)=cos(2π−x)、tan(x)=cot(2π−x)、sec(x)=csc(2π−x)
同样的我们也有
c o s ( x ) = s i n ( π 2 − x ) 、 c o t ( x ) = t a n ( π 2 − x ) 、 c s c ( x ) = s e c ( π 2 − x ) cos(x)=sin(\frac{\pi}{2}-x)、cot(x)=tan(\frac{\pi}{2}-x)、csc(x)=sec(\frac{\pi}{2}-x) cos(x)=sin(2π−x)、cot(x)=tan(2π−x)、csc(x)=sec(2π−x)
最后还有加法公式和二倍角公式。
加法公式我们有:
sin ( A + B ) = sin ( A ) cos ( B ) + cos ( A ) sin ( B ) cos ( A + B ) = cos ( A ) cos ( B ) − sin ( A ) sin ( B ) \sin(A+B)=\sin(A)\cos(B)+\cos(A)\sin(B)\\ \cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B) sin(A+B)=sin(A)cos(B)+cos(A)sin(B)cos(A+B)=cos(A)cos(B)−sin(A)sin(B)
同样的对于 A − B A-B A−B我们有
sin ( A − B ) = sin ( A ) cos ( B ) − cos ( A ) sin ( B ) cos ( A − B ) = cos ( A ) cos ( B ) + sin ( A ) sin ( B ) \sin(A-B)=\sin(A)\cos(B)-\cos(A)\sin(B)\\ \cos(A-B)=\cos(A)\cos(B)+\sin(A)\sin(B) sin(A−B)=sin(A)cos(B)−cos(A)sin(B)cos(A−B)=cos(A)cos(B)+sin(A)sin(B)
令 A = B A=B A=B,我们有 A + B = 2 A A+B=2A A+B=2A。根据加法公式我们有
sin ( 2 A ) = 2 sin ( A ) cos ( A ) \sin(2A)=2\sin(A)\cos(A) sin(2A)=2sin(A)cos(A)
cos ( 2 A ) = cos 2 ( A ) − sin 2 ( A ) \cos(2A)=\cos^2(A)-\sin^2(A) cos(2A)=cos2(A)−sin2(A)
对于第二个公式,我们可以使用勾股定理将它表示为
cos ( 2 A ) = 2 cos 2 ( A ) − 1 \cos(2A)=2\cos^2(A)-1 cos(2A)=2cos2(A)−1
或
cos ( 2 A ) = 1 − 2 sin 2 ( A ) \cos(2A)=1-2\sin^2(A) cos(2A)=1−2sin2(A)
如有问题,恳请指正