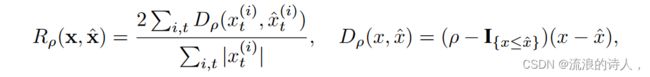Enhancing the Locality and Breaking the MemoryBottleneck of Transformer on Time Series Forecasting
本论文发表在33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada.
Abstract
时间序列预测是许多领域的一个重要问题,包括太阳能发电厂能源输出、电力消耗和交通拥堵情况的预测。在本文中,我们建议使用 Transformer [1] 来解决此类预测问题。尽管我们的初步研究对其性能印象深刻,但我们发现了它的两个主要弱点:
(1)局部性不可知论:规范 Transformer 架构中的点积自注意力对局部上下文不敏感,这可能使模型容易出现异常在时间序列中;
(2)内存瓶颈:规范Transformer的空间复杂度随着序列长度L呈二次方增长,使得直接建模长时间序列不可行。为了解决这两个问题,我们首先提出卷积自注意力,通过因果卷积产生查询和键,以便局部上下文可以更好地融入注意力机制中。然后,我们提出了 LogSparse Transformer,其内存成本仅为 O(L(log L)2),在内存预算受限的情况下提高了细粒度和强长期依赖关系的时间序列的预测精度。我们对合成数据和现实数据集的实验表明,它与最先进的技术相比毫不逊色。
- 相比于RNN,Transformer可以更好地建模长时间序列
- RNN 训练起来比较困难(梯度消失/梯度爆炸)
- RNN对于捕捉长期依赖关系比较困难
但是Transformer也有一定的问题:
- 局部性不可感知
- 存储空间瓶颈
- 传统Transformer的空间和时间复杂度是

- 这篇论文提出来的LogSparse Transformer 的内存消耗是
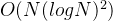
- 传统Transformer的空间和时间复杂度是
1 Introduction
时间序列预测在日常生活中发挥着重要作用,可以帮助人们管理资源和做出决策。例如,在零售行业,根据历史数据对产品需求和供应进行概率预测可以帮助人们进行库存计划以实现利润最大化。尽管仍然广泛使用,但传统的时间序列预测模型,例如状态空间模型(SSM)[2]和自回归(AR)模型,被设计为独立地拟合每个时间序列。此外,它们还需要从业者具有手动选择趋势、季节性和其他成分的专业知识。综上所述,这两个主要弱点极大地阻碍了它们在现代大规模时间序列预测任务中的应用。
为了解决上述挑战,深度神经网络[3-6]被提出作为替代解决方案,其中循环神经网络(RNN)[7-9]被用来以自回归方式对时间序列进行建模。然而,由于梯度消失和爆炸问题,RNN 的训练非常困难 [10]。尽管出现了各种变体,包括 LSTM [11] 和 GRU [12],但问题仍然没有得到解决。例如,[13]表明,使用 LSTM 的语言模型平均具有约 200 个 token 的有效上下文大小,但只能清晰地区分附近的 50 个 token,这表明即使 LSTM 也难以捕获长期依赖。另一方面,现实世界的预测应用程序通常具有长期和短期重复模式[7]。例如,交通数据中高速公路的每小时占用率既有每日模式,也有每小时模式。在这种情况下,如何对长期依赖关系进行建模成为实现有希望的性能的关键步骤。
最近,Transformer [1, 14] 被提出作为一种全新的架构,它利用注意力机制来处理数据序列。与基于 RNN 的方法不同,Transformer 允许模型访问历史的任何部分,无论距离如何,这使其更适合掌握具有长期依赖性的重复模式。然而,规范的点积自注意力将查询与对本地上下文不敏感的键进行匹配,这可能使模型容易出现异常并带来潜在的优化问题。更重要的是,规范 Transformer 的空间复杂度随着输入长度 L 呈二次方增长,这导致直接建模细粒度的长时间序列时出现内存瓶颈。我们专门深入研究这两个问题并研究 Transformer 在时间序列预测中的应用。我们的贡献有三方面:
我们成功地将 Transformer 架构应用于时间序列预测,并对合成数据集和真实数据集进行了广泛的实验,以验证 Transformer 在比基于 RNN 的模型更好地处理长期依赖性方面的潜在价值。
• 我们提出了卷积自注意力,通过使用因果卷积在自注意力层中产生查询和键。查询键匹配了解本地上下文,例如形状,可以帮助模型实现更低的训练损失并进一步提高其预测精度。
• 我们提出LogSparse Transformer,仅具有O(L(log L)2)空间复杂度来打破内存瓶颈,不仅使细粒度的长时间序列建模可行,而且可以用更少的内存使用产生类似甚至更好的结果,与规范 Transformer 相比。
2 Related Work
由于预测的广泛应用,人们提出了各种方法来解决该问题。最著名的模型之一是 ARIMA [15]。它的统计特性以及模型选择过程中众所周知的 Box-Jenkins 方法 [16] 使其成为从业者的首次尝试。然而,其线性假设和有限的可扩展性使其不适合大规模预测任务。此外,由于每个时间序列都是单独拟合的,因此无法共享相似时间序列的信息。相比之下,[17]将相关时间序列数据建模为矩阵,并将预测作为矩阵分解问题来处理。 [18]提出了从图模型的角度跨多个相关计数时间序列进行学习的分层贝叶斯方法。
深度神经网络已被提出来捕获相关时间序列中的共享信息,以进行准确的预测。 [3] 通过以编码器-解码器方式对概率分布进行建模,将传统 AR 模型与 RNN 融合。相反,[19]使用 RNN 作为编码器和多层感知器(MLP)作为解码器来解决所谓的误差累积问题并并行进行多提前预测。 [6]使用全局RNN直接输出每个时间序列每一步的线性SSM参数,旨在用局部线性段近似非线性动力学。相比之下,[9] 使用每个时间序列的局部高斯过程来处理噪声,同时使用全局 RNN 来对共享模式进行建模。 [20]试图结合AR模型和SSM的优点,并维护一个复杂的潜在过程来并行进行多步预测。
众所周知的基于自注意力的 Transformer [1] 最近被提出用于序列建模并取得了巨大的成功。最近的几部作品将其应用于翻译、语音、音乐和图像生成 [1, 21–23]。然而,将注意力扩展到极长的序列在计算上是令人望而却步的,因为自注意力的空间复杂度随着序列长度呈二次方增长[21]。这成为预测具有细粒度和强长期依赖性的时间序列的一个严重问题。
3 Background
Problem definition
- 假设有N个相关的时间序列
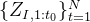 ,其中每个
,其中每个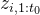 是时间序列i
是时间序列i ![[z_{i,1},\cdots,z_{i,t_0}]](http://img.e-com-net.com/image/info8/c099dbe098944fcab592bcf0b027bcdd.png)
- 任务是希望预测之后所有时间序列的τ时间步
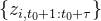
- 与此同时,令
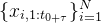 表示和时间序列相关联的向量(比如一周的哪一天,一天的哪个小时等)
表示和时间序列相关联的向量(比如一周的哪一天,一天的哪个小时等) - 计划是通过X和Z预测未来时间步的z
- 对于等式右侧各个条件概率,问题可以简化为:
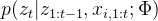
- 方便起见,我们把z和x合并成一个增广矩阵Y
Transformer
机器学习笔记:Transformer_embedding dimension-CSDN博客
文章利用多头自注意机制用Transformer 3实例化f,因为自注意使Transformer能够捕捉长期和短期的依赖关系,不同的注意头学习关注时间模式的不同方面。
预测时间序列的时候,我们是不能看到未来时间序列的信息的,所以这里的attention矩阵,上三角矩阵全是-∞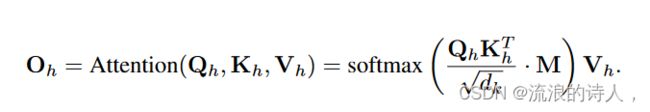
注意,为了避免将来的信息泄漏,通过将所有上三角元素设置为-![]() ,应用掩码矩阵M来滤除向右的关注。之后,O1;O2;···;OH是串联和线性投影的。在注意输出的基础上,叠加一个位置前馈子层,该子层由两层全连通网络和中间的ReLU激活组成。
,应用掩码矩阵M来滤除向右的关注。之后,O1;O2;···;OH是串联和线性投影的。在注意输出的基础上,叠加一个位置前馈子层,该子层由两层全连通网络和中间的ReLU激活组成。
4 Methodology
4.1 Enhancing the locality of Transformer
由于节假日和极端天气等各种事件的影响,时间序列中的模式会随着时间的变化而变化,因此,一个观察点是异常点、变化点还是模式的一部分,在很大程度上取决于其周围的环境。然而,在规范Transformer的自关注层中,queries和keys之间的相似性是基于它们的逐点值计算的,而没有充分利用局部上下文(如shape),如图1(a)和(b)所示。局部上下文的Query-key匹配不可知可能会混淆自注意模块的观测值是异常、变化点还是模式的一部分,并带来潜在的优化问题。
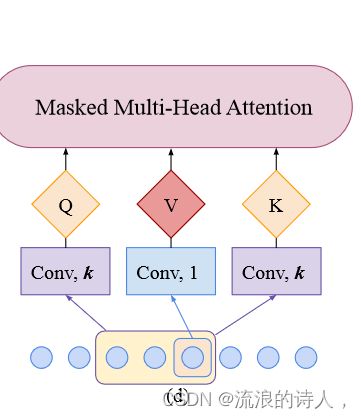
本文提出卷积自注意层来解决这个问题,图1(c)和(d)说明了提出的卷积式自我注意的架构视图。
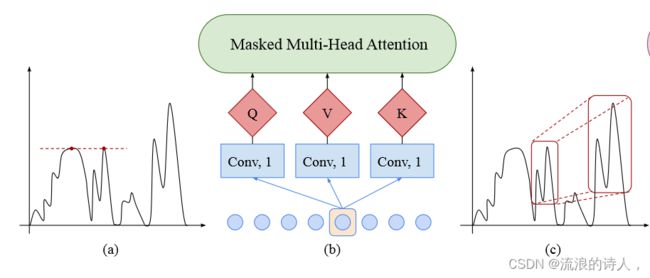 1. 传统的Transformer中,我们是对每个点单独进行Q,K,V的投影计算的。
1. 传统的Transformer中,我们是对每个点单独进行Q,K,V的投影计算的。
2.这导致的一个问题是,比如图(a)中的两个红点,他们尽管在时间序列上的特征不同(一个是陡增一个是缓趋势),但是由于绝对数值一样,所以算出来的两个attention是很接近的
3.而(c)中框起来的两块区域,他们的局部特征是很类似的,但是由于他们的绝对数值不一样,所以算出来的两个attention不大(但理论上应该是比较大的)
为了让Transformer的Q,K可以看到一定时间序列的局部特征,这里引入了卷积自注意力。
- 这里使用stride为1,kernel大小为k的因果卷积来计算Q和K。通过因果卷积,Q和K可以更好地知晓当前时刻的局部时间序列信息
- 传统Transformer可以看成这种情况的特例,即k=1的情况
本文使用kernel大小k的因果卷积(causal convolution)(步幅为1)将输入(使用适当的paddings)转换为queries和keys。请注意,因果关系会确保当前位置永远无法获得未来的信息。通过使用因果卷积,生成的queries和keys可以更好地感知局部上下文,从而通过局部上下文信息(如局部形状)来计算它们的相似性,而不是点状值,这有助于准确预测。注意,当k=1时,卷积自注意退化为规范自注意,因而可以看作是一个泛化过程。
4.2 Breaking the memory bottleneck of Transformer
为了验证方法,文章首先在TRAVINS-F数据集上用一个规范的transformer模型对学习到的注意力模式进行定性评估。traffic-f数据集包含旧金山湾区963条车道的占用率,每20分钟记录一次。我们训练了一个10层的典型变压器在TRAFF-F数据集上充分注意,并将学习到的注意模式可视化。图2中显示了一个示例。第2层清楚地显示了全局模式,然而,第6层和第10层只显示了依赖于模式的稀疏性,这表明可以在不显著影响性能的情况下引入某种形式的稀疏性。更重要的事,对于序列长度为L的序列,计算每对单元之间的注意力分数将导致O(L2)内存占用,使得对具有细粒度和强长期依赖性的长时间序列进行建模变得困难。
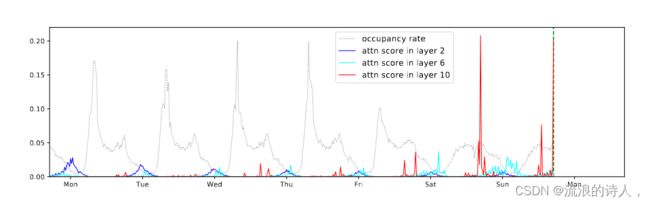
图 2:从 10 层规范 Transformer 中学习到的注意力模式,该 Transformer 在 Traffic-f 数据集上进行了充分的注意力训练。绿色虚线表示预测的开始时间,其左侧的灰色虚线是条件历史记录。当预测与绿色虚线对应的时间的值时,蓝色、青色和红色线分别对应于第 2、6 和 10 层中的注意力模式。 a) 第 2 层倾向于每天学习共享模式。 b) 第 6 层更关注周末模式。 c) 第 10 层进一步将大部分注意力集中在周末的几个单元上,导致其他大多数单元很少受到关注。
可以看到,在第二层的时候,attention可能还来自于很远处的时间片;但是到了第10层的时候,attention基本上就来自于局部的时间片了。
——>所以在进行attention的时候,一定的稀疏性可能不会很显著地影响结果
4.2.2 LogSparse Transformer
- 于是这篇论文提出了LogSparse Transformer
- 每一层的每一个单元只需要计算O(logL)次内积
- 最多迭代O(logL)层
- ——>所以总的空间复杂度是
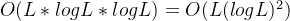
记![]() 为l时刻的单元从第k层到第k+1层所能看到的其他时间序列单元的集合
为l时刻的单元从第k层到第k+1层所能看到的其他时间序列单元的集合
- 传统Transformer中
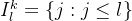
- 在这里,作者希望
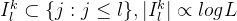
记![]() 表示第k层第l个单元可以看到的所有时间序列单元的集合
表示第k层第l个单元可以看到的所有时间序列单元的集合
- 如果最后一层,每一个l单元的
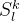 都包含了所有在它前面的时刻单元,那么就是一个有效的全局attention
都包含了所有在它前面的时刻单元,那么就是一个有效的全局attention - 换言之,任取单元l,和一个在l前面的时刻单元j,都有一条路径
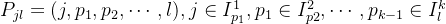
- LogSparse 自注意力的设计是,
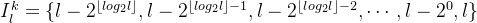
4.2.3 Local Attention
对cell前面的![]() 个点,我们也考虑他们的attention,这样的话局部的信息(比如trend),也可以被利用,同时不影响复杂度的级数
个点,我们也考虑他们的attention,这样的话局部的信息(比如trend),也可以被利用,同时不影响复杂度的级数
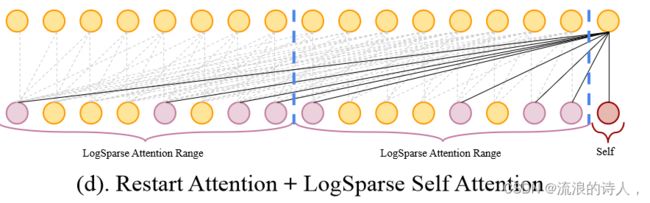
3.2.4 restart attention
将长时间序列拆分成几个subsequence,在每个subsequence里面使用LogSparse attention
local attention可以和 restart attention合并使用
5 Experiments
5.1 Synthetic datasets
为了证明 Transformer 捕获长期依赖性的能力,我们对合成数据进行了实验。具体来说,我们生成分段正弦信号
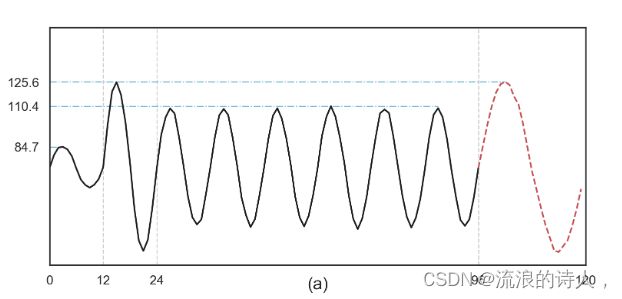
其中x为整数,A1、A2、A3在[0, 60]上均匀分布随机生成,A4 = max(A1, A2)且Nx ∼ N (0, 1)。按照第 3 节中的预测设置,我们的目标是根据之前的 t0 数据点预测最后 24 个步骤。直观上,较大的 t0 会使预测更加困难,因为模型需要理解并记住 A1 和 A2 之间的关系,以便在 t0 − 24 个不相关信号步骤后做出正确的预测。因此,我们通过在 {24, 48, 72, 96, 120, 144, 168, 192} 内改变 t0 的值来创建 8 个不同的数据集。对于每个数据集,我们分别生成 4.5K、0.5K 和 1K 时间序列实例用于训练、验证和测试集。图 4(a) 显示了 t0 = 96 的示例时间序列。
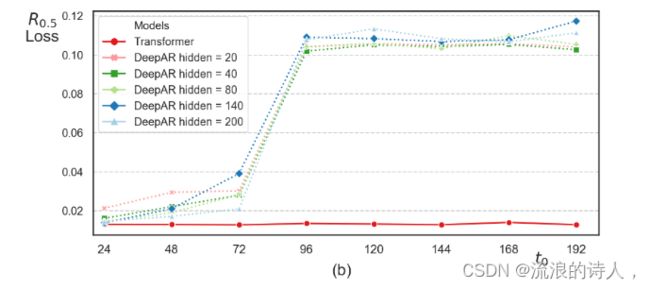
在这个实验中,我们使用具有标准自注意力的 3 层规范 Transformer。为了进行比较,我们采用 DeepAR [3](一种基于 3 层 LSTM 的自回归模型)作为我们的基线。此外,为了检验更大的容量是否可以提高 DeepAR 的性能,我们还逐渐增加其隐藏大小 h 为 {20, 40, 80, 140, 200}。按照[3, 6],我们使用 ρ 分位数损失 Rρ 和 ρ ε (0, 1) 来评估这两种方法,
在这个实验中,我们使用具有标准自注意力的 3 层规范 Transformer。为了进行比较,我们采用 DeepAR [3](一种基于 3 层 LSTM 的自回归模型)作为我们的基线。此外,为了检验更大的容量是否可以提高 DeepAR 的性能,我们还逐渐增加其隐藏大小 h 为 {20, 40, 80, 140, 200}。按照[3, 6],我们使用 ρ 分位数损失 Rρ 和 ρ ε (0, 1) 来评估这两种方法,
其中 ˆ x 是预测分布的经验 ρ 分位数,I{x≤ˆ x} 是指示函数。图 4:(a) t0 = 96 的时间序列示例。黑线是条件历史记录,红色虚线是目标。 (b)随着 t0 的增长,DeepAR 和规范 Transformer 之间的性能比较。 t0 越大,模型需要捕获的依赖关系就越长才能进行准确预测。图 4(b) 显示了 DeepAR 和 Transformer 在合成数据集上的性能。当t0 = 24时,两者都表现得很好。但是,随着 t0 的增加,尤其是当 t0 ≥ 96 时,DeepAR 的性能显着下降,而 Transformer 保持其准确性,这表明当 LSTM 无法做到这一点时,Transformer 可以捕获相当长期的依赖关系.
5.2 Real-world datasets
我们在几个现实世界的数据集上进一步评估我们的模型。电力-f(精细)数据集由每15分钟记录的370个客户的用电量组成,电力-c(粗略)数据集是电力-f每4个点的汇总,产生每小时的用电量。同样,traffic-f(精细)数据集包含每 20 分钟记录一次的旧金山 963 条高速公路的占用率,traffic-c(粗略)数据集包含对 Traffic-f 中每 3 个点进行平均的每小时占用率。太阳能数据集6包含2006年1月至8月的太阳能发电记录,每小时从阿拉巴马州137个光伏电站进行采样。
Long-term and short-term forecasting
 我们首先展示了配备卷积自注意力的规范 Transformer 在电力-c 和交通-c 数据集的长期和短期预测中的有效性。这两个数据集表现出每小时和每日的季节性模式。然而,与电力-c 相比,交通-c 在工作日和周末的模式之间表现出更大的差异。因此,traffic-c 数据集中的准确预测需要模型能够很好地捕获长期和短期依赖性。作为基线,我们使用 R 预测包中实现的经典预测方法 auto.arima、ets 和最近的矩阵分解方法 TRMF [17]、基于 RNN 的自回归模型 DeepAR 和基于 RNN 的状态空间模型 DeepState [6]。对于短期预测,我们评估 7 天的滚动日预测(即,预测范围为一天,预测开始时间在评估当天的预测后移动一天 [6])。对于长期预测,我们直接预测提前7天。如表1所示,与强基线相比,我们的具有卷积自注意力的模型在长期和短期预测方面都取得了更好的结果,特别是在traffic-c数据集上,部分原因在于Transformer的长期依赖建模能力如我们的合成数据所示。
我们首先展示了配备卷积自注意力的规范 Transformer 在电力-c 和交通-c 数据集的长期和短期预测中的有效性。这两个数据集表现出每小时和每日的季节性模式。然而,与电力-c 相比,交通-c 在工作日和周末的模式之间表现出更大的差异。因此,traffic-c 数据集中的准确预测需要模型能够很好地捕获长期和短期依赖性。作为基线,我们使用 R 预测包中实现的经典预测方法 auto.arima、ets 和最近的矩阵分解方法 TRMF [17]、基于 RNN 的自回归模型 DeepAR 和基于 RNN 的状态空间模型 DeepState [6]。对于短期预测,我们评估 7 天的滚动日预测(即,预测范围为一天,预测开始时间在评估当天的预测后移动一天 [6])。对于长期预测,我们直接预测提前7天。如表1所示,与强基线相比,我们的具有卷积自注意力的模型在长期和短期预测方面都取得了更好的结果,特别是在traffic-c数据集上,部分原因在于Transformer的长期依赖建模能力如我们的合成数据所示。
Convolutional self-attention
 在这个实验中,我们对我们提出的卷积自注意力进行了消融研究。我们在完整注意力模型上探索不同的内核大小 k ∈ {1, 2, 3, 6, 9} 并修复所有其他设置。我们仍然对电力-c 和交通-c 数据集使用 7 天的滚动日预测。两个数据集上不同内核大小的结果如表 2 所示。在 electric-c 数据集上,内核大小 k ∈ {2, 3, 6, 9} 的模型在 R0.5 方面获得比规范 Transformer 稍好的结果,但总体而言,这些结果具有可比性,并且都表现得非常好。我们认为这是因为 electric-c 数据集的挑战性较小,并且协变量向量已经为模型提供了丰富的信息以进行准确的预测。因此,在这种情况下,了解更大的当地背景可能没有多大帮助。然而,在更具挑战性的traffic-c数据集上,具有较大内核尺寸k的模型可以比具有较小内核尺寸的模型做出更准确的预测,相对改进高达9%。这些一致的收益可能是通过了解更多本地上下文进行更准确的查询键匹配的结果。此外,为了验证将更多本地上下文合并到查询键匹配中是否可以简化训练,我们绘制了在 electric-c 和 Traffic-c 数据集中训练内核大小 k ∈ {1, 3, 9} 的损失。我们发现具有卷积自注意力的 Transformer 也能更快地收敛并降低训练误差,
在这个实验中,我们对我们提出的卷积自注意力进行了消融研究。我们在完整注意力模型上探索不同的内核大小 k ∈ {1, 2, 3, 6, 9} 并修复所有其他设置。我们仍然对电力-c 和交通-c 数据集使用 7 天的滚动日预测。两个数据集上不同内核大小的结果如表 2 所示。在 electric-c 数据集上,内核大小 k ∈ {2, 3, 6, 9} 的模型在 R0.5 方面获得比规范 Transformer 稍好的结果,但总体而言,这些结果具有可比性,并且都表现得非常好。我们认为这是因为 electric-c 数据集的挑战性较小,并且协变量向量已经为模型提供了丰富的信息以进行准确的预测。因此,在这种情况下,了解更大的当地背景可能没有多大帮助。然而,在更具挑战性的traffic-c数据集上,具有较大内核尺寸k的模型可以比具有较小内核尺寸的模型做出更准确的预测,相对改进高达9%。这些一致的收益可能是通过了解更多本地上下文进行更准确的查询键匹配的结果。此外,为了验证将更多本地上下文合并到查询键匹配中是否可以简化训练,我们绘制了在 electric-c 和 Traffic-c 数据集中训练内核大小 k ∈ {1, 3, 9} 的损失。我们发现具有卷积自注意力的 Transformer 也能更快地收敛并降低训练误差,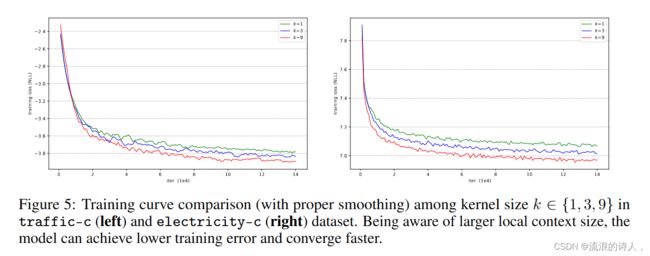 如图 5 所示,证明了解局部上下文可以简化训练过程。
如图 5 所示,证明了解局部上下文可以简化训练过程。
Sparse attention
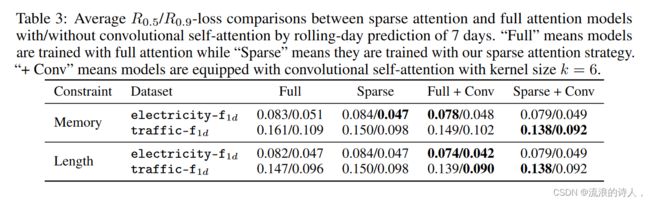 此外,我们将我们提出的 LogSparse Transformer 与细粒度数据集、electricity-f 和 Traffic-f 上的完全注意力对应物进行比较。请注意,与电力-c 和交通-c 相比,这两个数据集中的时间序列具有更长的周期并且噪声更大。我们首先在相同的内存预算下对它们进行比较。对于 electric-f 数据集,我们在稀疏注意力模型的每个子序列中选择 Le1 = 768,子序列长度 Le1 /8 和局部注意力长度 log2(Le1 /8),在全注意力模型中选择 Le2 = 293。对于traffic-f数据集,我们在稀疏注意力模型的每个子序列中选择Lt1 = 576,子序列长度为Lt1 /8,局部注意力长度为log2(Lt1 /8),在完整注意力模型中选择Lt2 = 254。内存使用量的计算和其他细节可以参见附录A.4。我们在两个数据集上对上述稀疏和全注意力模型(有/没有卷积自注意力)进行了实验。通过遵循这样的设置,我们将结果总结在表 3(上半部分)中。无论是否配备卷积自注意力,我们的稀疏注意力模型在电力-f上都取得了可比的结果,但与全注意力模型相比,在流量-f上取得了更好的结果。 Traffic-f 的这种性能提升可能是由于数据集更强的长期依赖性以及我们的稀疏模型更好的捕获这些依赖性的能力的结果,而在相同的内存预算下,完全注意力模型无法比拟。此外,稀疏注意力模型和全注意力模型都受益于具有挑战性的流量-f上的卷积自注意力,证明了其有效性。
此外,我们将我们提出的 LogSparse Transformer 与细粒度数据集、electricity-f 和 Traffic-f 上的完全注意力对应物进行比较。请注意,与电力-c 和交通-c 相比,这两个数据集中的时间序列具有更长的周期并且噪声更大。我们首先在相同的内存预算下对它们进行比较。对于 electric-f 数据集,我们在稀疏注意力模型的每个子序列中选择 Le1 = 768,子序列长度 Le1 /8 和局部注意力长度 log2(Le1 /8),在全注意力模型中选择 Le2 = 293。对于traffic-f数据集,我们在稀疏注意力模型的每个子序列中选择Lt1 = 576,子序列长度为Lt1 /8,局部注意力长度为log2(Lt1 /8),在完整注意力模型中选择Lt2 = 254。内存使用量的计算和其他细节可以参见附录A.4。我们在两个数据集上对上述稀疏和全注意力模型(有/没有卷积自注意力)进行了实验。通过遵循这样的设置,我们将结果总结在表 3(上半部分)中。无论是否配备卷积自注意力,我们的稀疏注意力模型在电力-f上都取得了可比的结果,但与全注意力模型相比,在流量-f上取得了更好的结果。 Traffic-f 的这种性能提升可能是由于数据集更强的长期依赖性以及我们的稀疏模型更好的捕获这些依赖性的能力的结果,而在相同的内存预算下,完全注意力模型无法比拟。此外,稀疏注意力模型和全注意力模型都受益于具有挑战性的流量-f上的卷积自注意力,证明了其有效性。
Further Exploration
 在我们的最后一个实验中,我们评估了我们的方法在不同粒度的数据集上与基线相比的表现。自提供M4-Hourly测试集以来,除M4-Hourly之外的所有数据集均通过滚动窗口评估7次。结果如表 4 所示。这些结果进一步表明我们的方法总体上达到了最佳性能。
在我们的最后一个实验中,我们评估了我们的方法在不同粒度的数据集上与基线相比的表现。自提供M4-Hourly测试集以来,除M4-Hourly之外的所有数据集均通过滚动窗口评估7次。结果如表 4 所示。这些结果进一步表明我们的方法总体上达到了最佳性能。
6 Conclusion
在本文中,我们建议将 Transformer 应用于时间序列预测。我们对合成数据和真实数据集的实验表明,Transformer 可以捕获长期依赖性,而 LSTM 可能会受到影响。我们还在现实数据集上表明,与最近基于 RNN 的方法(矩阵分解方法)相比,所提出的卷积自注意力进一步提高了 Transformer 的性能,并在不同的设置中实现了最先进的技术作为经典的统计方法。此外,在相同的内存预算下,我们的稀疏注意力模型可以在具有长期依赖性的数据上取得更好的结果。探索更好的自注意力稀疏策略并扩展我们的方法以更好地适应小数据集是我们未来的研究方向。