SVM线性支持向量机（二）（python实现）

3.求解根据带约束条件的目标函数最佳参数$\alpha$

在硬间隔的线性可分支持向量机和软间隔的支持向量机中我们通过拉格朗日函数，对偶问题将带约束条件的求解多个最优参数的目标函数转化求解一个最优参数的目标函数。式1.26和式2.8，当时没有解释如何求最优参数$\alpha$,这里使用SMO序列最小优化算法求解最佳参数$\alpha$，SMO算法是一种启发式算法，他与坐标下降法类似。

3.1坐标下降法

坐标下降法每次都更新一个参数，这里举一个例子，对于求解最优参数$x_1,x_2$使目标函数$f(x_1,x_2)$最小化问题
$$argmi{n}_{(x_1,x_2)}f(x_1,x_2)=x_1^2+2x_2^2-x_1{x}_2+1(3.1)$$
1…对于使用坐标下降法求解问题3.1的最优参数$x_1,x_2$,首先对$x_1,x_2$赋予一个初值$x_1^{(0)},x_2^{(0)}$

2.然后固定$x_2=x_2^{(0)}$，求解最优参数$x_1$使目标函数最小化
$$\begin{gathered} argmi{n}_{x_1}f(x_1,x_2^{(0)}) \\ =>\frac{\partial f(x_1,x_2^{(0)})}{\partial x_1}=2x_1-x_2=0(3.2) \\ =>x_1=\frac{x_2^{(0)}}{2} \end{gathered}$$
3.固定$x_1^{(1)}=x_1$,求解参数$x_2$，使得目标函数值最小
$$\begin{gathered} argmi{n}_{x_2}f(x_1^{(1)},x_2) \\ =>\frac{\partial f(x_1^{(1)},x_2}{\partial x_2}=4x_2-x_1^{(1)}=0(3.3) \\ =>x_2=\frac{x_1^{(1)}}{4} \end{gathered}$$
然后重复步骤2和步骤3，直到$x_1,x_2$值收敛。

3.2SMO序列最小优化算法

能不能使用坐标下降法求解最优参数$\alpha$？求解最优参数$\alpha$的问题为
$$\begin{gathered} maxL(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{\alpha }_j{y}_j{K}_{ij}(3.4) \\ s.t\sum _{i=1}^m{\alpha }_i{y}_i=00\le \alpha \le C(3.5) \end{gathered}$$
当使用坐标下降法求解参数$\alpha$时，先固定${\alpha }_2,{\alpha }_3,...{\alpha }_m$的参数值，再求出参数${\alpha }_1$使目标函数$L(\alpha )$值最大，但是发现在约束条件式3.5,当固定了${\alpha }_2,{\alpha }_3,...{\alpha }_m$参数值后，${\alpha }_1$的参数可以直接求出来，不能起到迭代求参数${\alpha }_2,{\alpha }_3,...,{\alpha }_m$,所以坐标下降法不适合求解该问题。SMO算法就是受到坐标下降法的启发，它的主要思想每次更新两个参数,固定${\alpha }_3,{\alpha }_4,...,{\alpha }_m,共m-2$个参数，再根据约束条件，确定剩下两个参数中的一个参数${\alpha }_2$，另一个参数${\alpha }_1$根据确定的参数${\alpha }_2$进行更新。

对于式3.5中固定${\alpha }_3,{\alpha }_4,...{\alpha }_m$参数值后，将${\alpha }_1,{\alpha }_2$提取出来
$$\begin{gathered} {\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^m{a}_i{y}_i=\epsilon \\ =>{\alpha }_1=y_1(\epsilon -{\alpha }_2{y}_2)(3.6) \end{gathered}$$
对与固定参数的${\alpha }_3,{\alpha }_4,...{\alpha }_m$,所以${\sum }_{i=3}^m{a}_i{y}_i$可以看作一个常数值$\epsilon$，对式3.6两边同乘$y_1$可以得出${\alpha }_1$的关系式，将式3.4中的${\alpha }_1,{\alpha }_2$提取出来
$$\begin{gathered} ma{x}_{({\alpha }_1,{\alpha }_2)}L({\alpha }_1,{\alpha }_2)={\alpha }_1+{\alpha }_2+\sum _{i=3}^m{\alpha }_i-\frac{1}{2}({\alpha }_1{y}_1{\alpha }_1{y}_1{K}_{11}+2{\alpha }_1{y}_1{\alpha }_2{y}_2{K}_{12} \\ +{\alpha }_2{y}_2{\alpha }_2{y}_2{K}_{22}+2\sum _{i=3}^m{\alpha }_1{y}_1{\alpha }_i{y}_i{K}_{1i}+2\sum _{i=3}^m{\alpha }_2{y}_2{K}_{2i}+\sum _{i=3}^m\sum _{j=3}^m{\alpha }_i{y}_i{\alpha }_j{y}_j{K}_{ij}(3.7) \end{gathered}$$
注意到${\alpha }_3,{\alpha }_4,...{\alpha }_m$参数值已经固定，${\sum }_{i=3}^m{\sum }_{j=3}^m{\alpha }_i{y}_i{\alpha }_j{y}_j{K}_{ij}-{\sum }_{i=3}^m{\alpha }_i$可以看作为是一个常数值，并且对于求解最优参数值${\alpha }_1,{\alpha }_2$使目标函数最大化无影响，式3.7可以进一步转化
$$\begin{gathered} ma{x}_{({\alpha }_1,{\alpha }_2)}{L}^{\prime }({\alpha }_1,{\alpha }_2)=ma{x}_{({\alpha }_1,{\alpha }_2)}L({\alpha }_1,{\alpha }_2)-C={\alpha }_1+{\alpha }_2-\frac{1}{2}({\alpha }_1{y}_1{\alpha }_1{y}_1{K}_{11}+2{\alpha }_1{y}_1{\alpha }_2{y}_2{K}_{12} \\ +{\alpha }_2{y}_2{\alpha }_2{y}_2{K}_{22}+2\sum _{i=3}^m{\alpha }_1{y}_1{\alpha }_i{y}_i{K}_{1i}+2\sum _{i=3}^m{\alpha }_2{y}_2{K}_{2i}(3.8) \end{gathered}$$
将式3.6得到的${\alpha }_1$的关系式代入式3.8中，可以将目标函数转化为只含有一个参数${\alpha }_2$
$$\begin{gathered} ma{x}_{{\alpha }_2}{L}^{\prime \prime }({\alpha }_2)=y_1(\epsilon -{\alpha }_2{y}_2)+{\alpha }_2-\frac{1}{2}[(\epsilon -{\alpha }_2{y}_2{)}^2{y}_1{K}_{11}+2(\epsilon -{\alpha }_2{y}_2){\alpha }_2{y}_2{K}_{12} \\ +{\alpha }_2^2{K}_{22}+2\sum _{i=3}^m(\epsilon -{\alpha }_2{y}_2){\alpha }_i{y}_i{K}_{1i}+2\sum _{i=3}^m{\alpha }_2{y}_2{K}_{2i}](3.9) \end{gathered}$$
3.9式对${\alpha }_2$求偏导并令其等于0有
$$\begin{gathered} \frac{\partial L^{\prime \prime }}{{\alpha }_2}=-y_1{y}_2+1-\frac{1}{2}[-2(\epsilon -{\alpha }_2{y}_2)y_2{K}_{11}+2(\epsilon -{\alpha }_2{y}_2){\alpha }_2{y}_2{K}_{12}-2{\alpha }_2{K}_{12} \\ -2y_2\sum _{i=3}^m{\alpha }_i{y}_i{K}_{1i}+2{\alpha }_2{K}_{22}+2y_2\sum _{i=3}^m{\alpha }_i{y}_i{K}_{2i}] \\ =1-y_1{y}_2+\epsilon y_2(K_{11}-K_{12})-{\alpha }_2(K_{11}+K_{22}-2K_{12})+\sum _{i=3}^m{y}_2{\alpha }_i{y}_i{K}_{1i}-\sum _{i=3}^m{y}_2{\alpha }_i{y}_i{K}_{2i}=0(3.10) \end{gathered}$$
由于再求解参数${\alpha }_1,{\alpha }_2$的过程中是在迭代过程中先求解参数${\alpha }_2$,再求解${\alpha }_1$，直到两者收敛，所以在迭代过程中永远满足式3.6的第一个等式，所以$\epsilon$可以使用在之前迭代求出来的${\alpha }_1,{\alpha }_2$代替
$$\begin{gathered} {\alpha }_1^{old}{y}_1+{\alpha }_2^{old}{y}_2=\epsilon (3.11) \\ {\alpha }_2^{new}(K_{11}+K_{22}-2K_{12})=1-y_1{y}_2+y_1{y}_2{\alpha }_1^{old}{K}_{11}-y_1{y}_2{\alpha }_1^{old}{K}_{12}+{\alpha }_2^{old}{K}_{11}-{\alpha }_2^{old}{K}_{12} \\ +\sum _{i=3}^m{y}_2{\alpha }_i{y}_i{K}_{1i}-\sum _{i=3}^m{y}_2{\alpha }_i{y}_i{K}_{2i}(3.12) \end{gathered}$$
对于式3.12中尾部出现两个累加项，并不希望这两个累加项的出现，注意这两个累加项，如果在式中凑一个$+b,-b,{\alpha }_1{y}_1{K}_{11}+{\alpha }_2{y}_2{K}_{12},{\alpha }_1{y}_1{K}_{12}+{\alpha }_2{y}_2{K}_{22}$刚好可以将这两累加项转化为样本$x_1,x_2$的预测值$f(x_1),f(x_2)$
$$\begin{gathered} {\alpha }_2^{new}(K_{11}+K_{22}-2K_{12})=1-y_1{y}_2+y_1{y}_2{\alpha }_1^{old}{K}_{11}-y_1{y}_2{\alpha }_1^{old}{K}_{12}+{\alpha }_2^{old}{K}_{11}-{\alpha }_2^{old}{K}_{12} \\ +y_2({\alpha }_1^{old}{y}_1{K}_{11}+{\alpha }_2^{old}{y}_2{K}_{12}+\sum _{i=3}^m{\alpha }_i{y}_i{K}_{1i}+b)-{\alpha }_1^{old}{y}_1{y}_2{K}_{11}-{\alpha }_2^{old}{K}_{12} \\ -y_2({\alpha }_1^{old}{y}_1{K}_{12}+{\alpha }_2^{old}{y}_2{K}_{22}+\sum _{i=3}^m{\alpha }_i{y}_i{K}_{2i}+b)+{\alpha }_1^{old}{y}_1{y}_2{K}_{12}+{\alpha }_2^{old}{K}_{22}(3.13) \\ =1-y_1{y}_2+y_1{y}_2{\alpha }_1^{old}{K}_{11}-y_1{y}_2{\alpha }_1^{old}{K}_{12}+{\alpha }_2^{old}{K}_{11}-{\alpha }_2^{old}{K}_{12} \\ +y_{2}f(x_1)-y_{2}f(x_2)-{\alpha }_1^{old}{y}_1{y}_2{K}_{11}-{\alpha }_2^{old}{K}_{12}+{\alpha }_1^{old}{y}_1{y}_2{K}_{12}+{\alpha }_2^{old}{K}_{22} \end{gathered}$$
对等式3.13化简，这里需要技巧将$1=y_2{y}_2$
$$\begin{gathered} {\alpha }_2^{new}(K_{11}+K_{22}-2K_{12})=1-y_1{y}_2+{\alpha }_2^{old}{K}_{11}-2{\alpha }_2^{old}{K}_{12}+y_{2}f(x_1)-y_{2}f(x_2)+{\alpha }_2^{old}{K}_{22} \\ =y_2[(f(x_1)-y_1)-(f(x_2)-y_2)]+{\alpha }_2^{old}(K_{11}+K_{22}-2K_{12})(3.14) \end{gathered}$$
对于式3.14中令$\eta =K_{11}+K_{22}-2K_{12}$,预测值与实际值的误差$E_i=f(x_i)-y_i$式3.14可以转化为
$${\alpha }_2^{new}=\frac{y_2(E_1-E_2)}{\eta }+{\alpha }_2^{old}(3.15)$$
这里求解出来的参数${\alpha }_2^{new}$是没有考虑约束条件的，现在需要考虑约束条件，也就是式3.5
$$\begin{gathered} \sum _{i=1}^m{\alpha }_i{y}_i=0=>{\alpha }_1{y}_1+{\alpha }_2{y}_2=\epsilon (3.16) \\ 0\le {\alpha }_1\le C0\le {\alpha }_2\le C(3.17) \end{gathered}$$
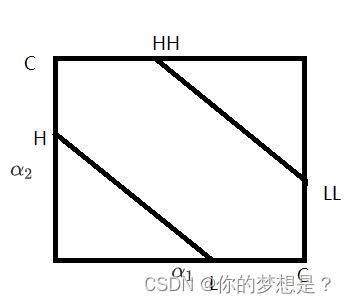
对于式3.17的约束条件，如果将${\alpha }_1,{\alpha }_2$分分别作为横纵坐标，那么它的可行域为

当加上式3.16的约束条件后，需要对$y_1,y_2$讨论

1.当$y_1=y_2$时，式3.16就是斜率为145度的直线${\alpha }_1+{\alpha }_2=y_1\epsilon =k$

在此时的约束条件下，${\alpha }_2$的最小值要么在L点或者LL点取到$L=max(0,k-C)=max(0,{\alpha }_1^{old}+{\alpha }_2^{old}-C)$,${\alpha }_2$的最大值要么在H点或者要么在HH点取到$H=min(C,{\alpha }_1^{old}+{\alpha }_2^{old})$

2.当$y_1\ne y_2$时，式3.16就是斜率为45度的直线${\alpha }_1-{\alpha }_2=y_1\epsilon =k$

在此时的情况下，${\alpha }_2$的最小值在L点或者LL点取到$L=max(0,-k)=max(0,{\alpha }_2^{old}-{\alpha }_1^{old})$${\alpha }_2$的最大值要么在H点或者要么在HH点取到$H=min(C,C-k)=min(C,C-{\alpha }_1^{old}+{\alpha }_2^{old})$

综上所述，筛选约束条件后的${\alpha }_2^{new}$
$${\alpha }_2^{new}=\{\begin{array}{ll}H& {\alpha }_2^{new}>H\\ {\alpha }_2^{new}& L\le x\le H\\ L& {\alpha }_2^{new}<L\end{array}(3.18)$$
参数${\alpha }_1^{new}$的求解需要利用到约束条件3.16，两边同乘$y_1$
$${\alpha }_1^{new}+y_1{y}_2{\alpha }_2^{new}=y_1\epsilon (3.19)$$
注意到$\epsilon$的值可以利用上一组${\alpha }_1,{\alpha }_2$的值代入
$${\alpha }_1^{new}=y_1(y_1{\alpha }_1^{old}+{\alpha }_2^{old}{y}_2)-y_1{y}_2{\alpha }_2^{new}={\alpha }_1^{old}+y_1{y}_2({\alpha }_2^{old}-{\alpha }_2^{new})(3.20)$$

3.3求解参数$w，b$

参数$w$的更新需要先迭代求出所有的最优参数$\alpha$,然后利用公式3.21即可求出参数$w$
$$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i(3.21)$$
在前面探讨求解参数$b$的过程都是利用支持向量来求解的，这里也不例外，在加入软间隔后，我们就需要2.2小节的方法判断下是数据点是否是支持向量，对于$0<\alpha <C$的情况下肯定是支持向量，对于求出来的${\alpha }_1,{\alpha }_2$都需要判断下是否满足$0<\alpha <C$，如果有一个满足的化，就让满足的$\alpha$求解$b$,如果都不满足，意思就是这两个数据样本对应的$\alpha$=0或者=C说明这两个数据样本可能是支持向量，如果都是支持向量根据这个两个$\alpha$求出来的$b$一定是相等的，所以取两个$\alpha$求出的$b$的平均数。对于${\alpha }_1$求b
$$\begin{gathered} b_1^{new}=y_1-\sum _{j=1}^m{\alpha }_j{y}_j{K}_{1i} \\ =y_1-{\alpha }_1^{new}{y}_1{K}_{11}-{\alpha }_2^{new}{y}_2{K}_{12}-\sum _{i=3}^m{\alpha }_i{y}_i{K}_{1i}(3.22) \end{gathered}$$
对于式3.21中我们并不希望${\sum }_{i=3}^m{\alpha }_i{y}_i{K}_{1i}$出现，为了消除它，可以利用之前求参数${\alpha }_2$过程中的思想，对3.21式中凑参数，添加上一组的$b$对式3.21中凑$+b^{old},-b^{old},{\alpha }_1^{old}{y}_1{K}_{11}+{\alpha }_2^{old}{y}_2{K}_{12}$
$$\begin{gathered} b_1^{new}=y_1-{\alpha }_1^{new}{y}_1{K}_{11}-{\alpha }_2^{new}{y}_2{K}_{12}+b^{old}+{\alpha }_1^{old}{y}_1{K}_{11}+{\alpha }_2^{old}{y}_2{K}_{12} \\ -({\alpha }_1^{old}{y}_1{K}_{11}+{\alpha }_2^{old}{y}_2{K}_{12}+\sum _{i=3}^m{\alpha }_i{y}_i{K}_{1i}+b)(3.23) \end{gathered}$$
注意到式3.22中括号中刚好是数据样本$x_1$根据上一组参数的预测值$f(x_1)$,$y_1-f(x_1)$刚好又是在计算式3.15中定义的误差$-E_1$,对式3.22变形有
$$b_1^{new}=-E_1-y_1{K}_{11}({\alpha }_1^{new}-{\alpha }_1^{old})-y_2{K}_{12}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old}(3.24)$$
同理，跟据${\alpha }_2^{new}$求得的参数$b$为$b_2^{new}$
$$b_2^{new}=-E_2-y_1{K}_{12}({\alpha }_1^{new}-{\alpha }_1^{old})-y_2{K}_{22}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old}(3.25)$$
所以参数$b$的值为
KaTeX parse error: Can't use function '\(' in math mode at position 218: …\alpha_1=C)\&\&\̲(̲alpha_2=0||\alp…

3.4如何选择更新$\alpha$

目前已经知道如何更新参数$\alpha ,w,b$,但是如何选$\alpha$进行更新?在SMO算法中对于第一个$\alpha$的选取违反KKT条件最严重的样本点进行更新
$$\begin{gathered} KKT条件： \\ {\partial }_{(w,b,\zeta ,\alpha ,{\mu }_i)}L=0(3.27) \\ {\alpha }_i(1-{\zeta }_i-y_i(w^T{x}_i+b))=0(3.28) \\ -{\zeta }_i\le 0(3.29) \\ {\mu }_i{\zeta }_i=0(3.30) \\ (1-{\zeta }_i-y_i(w^T{x}_i+b))\le 0(3.31) \\ {\alpha }_i\ge 0(3.32) \\ {\mu }_i\ge 0(3.33) \\ i\in \{1,2,...m\} \end{gathered}$$

按照这个KKT条件，可以推导出关于$\alpha$的与支持向量间的关系，在2.2节已经推导过一次，这里就不在推导了
$$\begin{gathered} {\alpha }_i=0<=>y_i(w^T{x}_i+b)\ge 1 \\ 0<{\alpha }_i<C<=>y_i(w^T{x}_i+b)=1(3.31) \\ {\alpha }_i=C<=>y_i(w^T{x}_i+b)\le 1 \end{gathered}$$
我自己的理解第一个$\alpha$选取是选择违反KKT条件最严重的点那么首先考虑$0<{\alpha }_i<C$的情况下，违反KKT最严重也就是
$$\begin{gathered} (0<{\alpha }_i\&\&y_i(w^T{x}_i+b)-1!=0)||(({\alpha }_i<C\&\&y_i(w^T{x}_i+b)-1!=0)) \\ =>(0<{\alpha }_i\&\&y_i((w^T{x}_i+b)-y_i)!=0)||(({\alpha }_i<C\&\&y_i((w^T{x}_i+b)-y_i)!=0)) \\ =>(0<{\alpha }_i\&\&y_i{E}_i!=0)||(({\alpha }_i<C\&\&y_i{E}_i!=0))(3.32) \end{gathered}$$
而在《机器学习实战》中给源码确是
$$(0<{\alpha }_i\&\&y_i(w^T{x}_i+b)-1\ge -\varsigma )||(({\alpha }_i<C\&\&y_i(w^T{x}_i+b)-1\le \varsigma ))(3.33)$$
其中$\varsigma$是精度，按照博客：支持向量机原理详解(六): 序列最小最优化(SMO)算法(Part I) - 知乎 (zhihu.com)有讲解，但是我不理解为什么要加入精度，按照我理解的式3.31貌似对程序结果没有影响（希望大佬留言）

4.SMO算法代码

#导入科学计算包
from numpy import *
#导入matplotlb绘图包
import matplotlib.pyplot as plt
#读取文件数据集
def load_data(file_name):
    #定义并初始化训练数据集
    data_mat=[]
    #定义并初始化标签数据集
    label_mat=[]
    #打开文件
    f=open(file_name)
    #对每一行数据迭代
    for line in f.readlines():
        #按制表符切分每一行数据
        line_cur=line.strip().split('\t')
        #将数每一个样本的据添加到数据集中
        data_mat.append([float(line_cur[0]),float(line_cur[1])])
        #将标签数据添加到标签数据集中
        label_mat.append(float(line_cur[2]))
    return data_mat,label_mat
#用对象来保存重要的属性值
class opt_struct:
    #构造函数
    def __init__(self,dataMatIn,classLabels,C,toler):
        self.X=dataMatIn
        self.labelMat=classLabels
        self.C=C
        self.tol=toler
        self.m=shape(dataMatIn)[0]
        self.alphas=mat(zeros((self.m,1)))
        self.b=0
        self.eCache=mat(zeros((self.m,2)))
#计算E值
def calcEk(os,k):
    #计算预测fk
    fXK=float(multiply(os.alphas,os.labelMat).T*os.X*os.X[k,:].T)+os.b
    #计算误差Ek
    Ek=fXK-float(os.labelMat[k])
    return Ek
#对alpha2进行修建操作
def clip_alpha(a_j,H,L):
    #如果alpha2大于最大值，修剪为最大值
    if a_j>H:
        a_j=H
    # 如果alpha2小于最小值，修剪为最小值
    if L>a_j:
        a_j=L
    return a_j
#随机选择第二个alpha进行迭代更新
def selectJrand(i,m):
    #定义第二个alpha下标并初始化为第一个下标值
    j=i
    #当第一个alpha下标和第二个alpha下标一致时，迭代选择第二个alpha
    while(j==i):
        #随机选择第二个alpha下标
        j=int(random.uniform(0,m))
    return j
#用于选择第二个alpha
def selectJ(i,os,Ei):
    #定义并初始化最大在最大步长时的alphaj的下标
    maxK=-1
    #定义并初始化最大步长
    maxDeltaE=0
    #定义并初始化第二个alpha的误差
    Ej=0
    #将第一个alpha的误差存入误差缓存列表中，并设置标志位为有效值
    os.eCache.tolist()[i]=[1,Ei]
    #获取误差缓存中所有标志有效的误差下标列表
    validEcacheList=nonzero(os.eCache[:,0].A)[0]
    #如果标志有效的下标误差列表至少有两个值
    if(len(validEcacheList))>1:
        #迭代标志有效的误差下标列表
        for k in validEcacheList:
            #如果下标与i相同，该轮迭代结束，进入下一轮
            if k==i:
                continue
            #计算下标为k的误差Ek
            Ek=calcEk(os,k)
            #定义差值来存储步长
            deltaE=abs(Ei-Ek)
            #如果步长大于最大步长
            if (deltaE>maxDeltaE):
                #将下标k赋值为在最大步长时的alphaj的下标
                maxK=k
                #将该步长赋值为最大步长
                maxDeltaE=deltaE
                #将该误差赋值为第二个alpha的误差
                Ej=Ek
        return maxK,Ej
    else:
        #如果标志有效的下标误差列表只有一个，即首次选择第二个alpha,则随机选择第二个alpha
        j=selectJrand(i,os.m)
        #计算第二个alpha的的误差
        Ej=calcEk(os,j)
    return j,Ej
#更新误差存入缓存中
def updateEk(os,k):
    #计算第k个误差
    Ek=calcEk(os,k)
    #将第k个误差存入误差缓存中，标志位设置为有效
    os.eCache.tolist()[k]=[1,Ek]
#SMO内循环代码
def innerL(i,os):
    #计算第一个alpha的误差
    Ei=calcEk(os,i)
    #选择违反KKT条件最严重的那个alpha进行优化
    if((os.labelMat[i]*Ei!=0) and (os.alphas[i]<os.C)) or \
            ((os.labelMat[i]*Ei!=0) and (os.alphas[i]>0)):
        # 根据启发式方法选择第二个alpha
        j,Ej=selectJ(i,os,Ei)
        #保存第一个alpha的old值
        alphaIold=os.alphas[i].copy()
        #保存第二个alpha的old值
        alphaJold=os.alphas[j].copy()
        #如果y1!=y2
        if(os.labelMat[i]!=os.labelMat[j]):
            #第二个alpha值的范围
            L=maximum(0,os.alphas[j]-os.alphas[i])
            H=minimum(os.C,os.C+os.alphas[j]-os.alphas[i])
        else:
            L=maximum(0,os.alphas[j]+os.alphas[i]-os.C)
            H=minimum(os.C,os.alphas[j]+os.alphas[i])
        #如果最小值和最大值相等，则第二个alpha值已经是最优的
        if L==H:
            return 0
        #计算eta值
        eta=2.0*os.X[i,:]*os.X[j,:].T-os.X[i,:]*os.X[i,:].T-os.X[j,:]*os.X[j,:].T
        #eta不能等于0
        if eta>=0:
            return 0
        #迭代更新第二个alpha值
        os.alphas[j]=os.alphas[j]-os.labelMat[j]*(Ei-Ej)/eta
        #对第二个alpha进行修剪操作
        os.alphas[j]=clip_alpha(os.alphas[j],H,L)
        #对修剪后的第二个alpha更新误差
        updateEk(os,j)
        #如果改变的范围不够大，默认没改变
        if(abs(os.alphas[j]-alphaJold)<0.00001):
            return 0
        #对第一个alpha进行迭代更新
        os.alphas[i]=os.alphas[i]+os.labelMat[j]*os.labelMat[i]*(alphaJold-os.alphas[j])
        #对更新后的第一个alpha更新误差
        updateEk(os,i)
        #根据第一个误差迭代更新b
        b1=os.b-Ei-os.labelMat[i]*(os.alphas[i]-alphaIold)*os.X[i,:]*os.X[i,:].T\
            -os.labelMat[j]*(os.alphas[j]-alphaJold)*os.X[i,:]*os.X[j,:].T
        #根据第二个误差迭代更新b
        b2 = os.b - Ej - os.labelMat[i] * (os.alphas[i] - alphaIold) * os.X[i, :] * os.X[j, :].T \
             - os.labelMat[j] * (os.alphas[j] - alphaJold) * os.X[j, :] * os.X[j, :].T
        #若第一个alpha是支持向量
        if(0<os.alphas[i])and(os.C>os.alphas[i]):
            os.b=b1
        #若第二个alpha是支持向量
        elif(0<os.alphas[j])and(os.C>os.alphas[j]):
            os.b=b2
        #若都不是支持向量
        else:
            os.b=(b1+b2)/2.0
        #返回1表示优化成功
        return 1
    #返回0表示优化失败
    else:
        return 0
#SMO外循环代码
def smoP(dataMat,classLabels,C,toler,maxIter):
    #获取存有属性值的对象
    os=opt_struct(mat(dataMat),mat(classLabels).transpose(),C,toler)
    #定义并初始化迭代次数
    iter=0
    #定义遍历整个集合标志位
    entireSet=True
    #定义并初始化alpha优化对数
    alphasPairsChanged=0
    #循环结束条件(当迭代次数大于最大迭代次数或者遍历了整个集合都没alpha更新
    while(iter<maxIter) and ((alphasPairsChanged>0) or (entireSet)):
        #每一次循环初始化alpha更新对数为0
        alphasPairsChanged=0
        #如果没有遍历遍历整个集合
        if entireSet:
            #对所有的alpha迭代
            for i in range(os.m):
                #选取下标为i的alpha作为第一个alpha,同时调用内循环，内循环返回更新结果
                alphasPairsChanged+=innerL(i,os)
            print(f"alpha集合遍历完毕，{alphasPairsChanged}对alpha发生改变,entireSet是{entireSet}")
            #迭代次数加一
            iter+=1
        #如果遍历了整个集合，则选择非边界alpha
        else:
            #获取在非边界条件上的alpha下标列表
            nonBoundIs=nonzero((os.alphas.A>0)*(os.alphas.A<C))[0]
            #对下标列表迭代
            for i in nonBoundIs:
                #将下标i作为第一个alpha，并且记录更新alpha的对数
                alphasPairsChanged+=innerL(i,os)
            print(f"非边界alpha遍历完毕，{alphasPairsChanged}对alpha发生改变")
            #迭代次数加一
            iter+=1
        #如果遍历完整个集合
        if entireSet:
            #对遍历整个集合的标志位修改位遍历完标志位
            entireSet=False
        #如果没有遍历完整个集合且更新alpha对数位0，需要遍历整个集合
        elif(alphasPairsChanged==0):
            entireSet=True
        print(f"迭代次数{iter}")
    return os.b,os.alphas
#绘图
def ploter(data,label,w,b):
    # 设置中文
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    m=len(data)
    data_mat=mat(data)
    x_list=list()
    y_list=list()
    label_data=mat(label).transpose()
    for i in range(m):
        if label[i]==1:
            plt.scatter(data[i][0],data[i][1],color='green')
        else:
            plt.scatter(data[i][0],data[i][1],color='blue')
    x = arange(10)

    # 根据x.w + b = 0 得到，其式子展开为w0.x1 + w1.x2 + b = 0, x2就是y值
    y = (-b - w[0, 0] * x) / w[1, 0]

    plt.plot(x, y.tolist()[0])

    # 找到支持向量，并在图中标黄
    for i in range(100):
        if alphas[i] > 0.0:
            plt.plot(data_mat[i, 0], data_mat[i, 1],marker='s',markersize=8,color='yellow')

    plt.show()
#计算w值
def calc_w(data,label,alphas):
    X = mat(data)
    labelMat = mat(label).transpose()
    m, n = shape(X)
    w = zeros((n, 1))

    for i in range(m):
        w += multiply(alphas[i] * labelMat[i], X[i, :].T)
    # print(multiply(alphas[i] * labelMat[i], X[i, :].T))
    return w

#测试
if __name__=='__main__':
    data,label=load_data("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch06/testSet.txt")
    b,alphas=smoP(data,label,0.6,0.001,40)
    w = calc_w(data, label, alphas)
    print(b)
    # print(alphas[alphas>0])
    ploter(data, label, w, b)
    #预测
    print(data[0]*mat(w)+b)
    print(label[0])

支持向量在图中使用黄色标出

5.总结

线性支持向量机的目标是找到一个最优的超平面，使得两个类别的样本能够尽可能地被完美地分开，并且两个类别样本离超平面的距离最大化。这个距离可以被称为间隔 (margin)。通过寻找最大间隔超平面，线性支持向量机能够在新的未知样本上取得较好的分类性能。在实际应用中，如果数据不是线性可分的，可以通过核函数 (Kernel Function) 将数据映射到高维空间中，从而使其在高维空间中线性可分。线性支持向量机
参考视频：简博士8 支持向量机（31）：SMO算法中参数变量的选择.MP4_哔哩哔哩_bilibili

参考书籍：《机器学习实战》peter,《机器学习》周志华，《统计学习方法》李航

参考博客：(33条消息) 支持向量机（SVM）—— 详细推导及案例应用可视化_svm算法应用实例_不会三刀流的索隆的博客-CSDN博客

​ 【机器学习】支持向量机 SVM（非常详细） - 知乎 (zhihu.com)

​ 支持向量机原理详解(一): 间隔最大化，支持向量 - 知乎 (zhihu.com)

​ 支持向量机原理详解(二): 拉格朗日对偶函数，SVM的对偶问题 - 知乎 (zhihu.com)

​ 支持向量机原理详解(七): 序列最小最优化(SMO)算法(Part II) - 知乎 (zhihu.com)

​ 支持向量机原理详解(六): 序列最小最优化(SMO)算法(Part I) - 知乎 (zhihu.com)