研习代码 day13 | 二叉树层序遍历的应用 && 翻转二叉树 && 对称二叉树
一、二叉树的层序遍历
1.1 题目
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
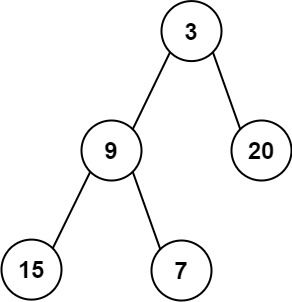
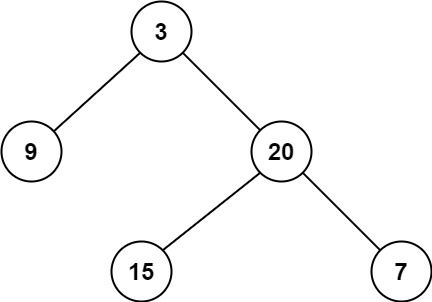
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
1.2 题目链接
102.二叉树的层序遍历
1.3 解题思路和过程想法
(1)解题思路:
借用队列存储当前层的结点,当前队列中的结点数量为本层需操作处理次数,在出队当前层结点的同时,将其左右孩子入队,从而获得层序遍历的结果。
(2)过程想法:
之前学过数据结构,直接手撕皆可。
1.4 代码
from queue import Queue
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
myQueue = Queue()
res = []
if root:
myQueue.put(root)
while not myQueue.empty():
# 记录该层的结点情况
level = []
size = myQueue.qsize()
# 上一层有多少个元素,就对应增加多少个结点的左右孩子
for i in range(size):
# 出队的同时,将其左右孩子入队
cur = myQueue.get()
level.append(cur.val)
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
res.append(level)
return res
二、二叉树的层序遍历 II
2.1 题目
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
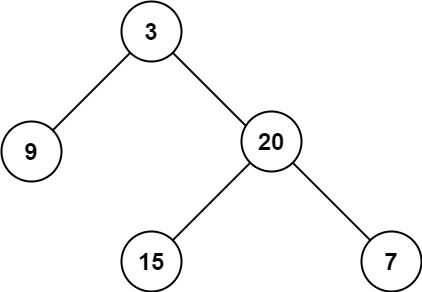
输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
2.2 题目链接
107.二叉树的层序遍历 II
2.3 解题思路和过程想法
(1)解题思路:
因所要结果就是层序遍历的逆置,所以考虑先用层序遍历得到结果,再使用栈将其逆置。
(2)过程想法:
思路比较简单,想法比较自然。
2.4 代码
from queue import Queue
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
# 因所要结果就是层序遍历的逆置,所以考虑先用层序遍历得到结果,再使用栈将其逆置
# 存储最后结果
res = []
# 用于逆置的栈
mystack = []
# 用于层序遍历的队列
myqueue = Queue()
if root:
myqueue.put(root)
# 层序遍历
while not myqueue.empty():
level = []
size = myqueue.qsize()
for i in range(size):
cur = myqueue.get()
level.append(cur.val)
if cur.left:
myqueue.put(cur.left)
if cur.right:
myqueue.put(cur.right)
mystack.append(level)
# 将层序遍历所得结果逆置
for i in range(len(mystack)):
res.append(mystack.pop())
return res三、二叉树的右视图
3.1 题目
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4] 输出: [1,3,4]
示例 2:
输入: [1,null,3] 输出: [1,3]
示例 3:
输入: [] 输出: []
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
3.2 题目链接
199.二叉树的右视图
3.3 解题思路和过程想法
(1)解题思路:
在层序遍历的基础上,将每层最后一个结点追加至结果列表。
(2)过程想法:
思路比较简单,想法比较自然。
3.4 代码
from queue import Queue
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
# 在层序遍历的基础上,将每层最后一个结点追加至结果列表
# 用于存储结果
res = []
# 用于遍历的队列
myQueue = Queue()
if root:
myQueue.put(root)
while not myQueue.empty():
level = []
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
level.append(cur.val)
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
res.append(level[-1])
return res四、二叉树的层平均值
4.1 题目
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:[3.00000,14.50000,11.00000] 解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。 因此返回 [3, 14.5, 11] 。
示例 2:
输入:root = [3,9,20,15,7] 输出:[3.00000,14.50000,11.00000]
提示:
- 树中节点数量在
[1, 104]范围内 -2^31 <= Node.val <= 2^31 - 1
4.2 题目链接
637.二叉树的层平均值
4.3 解题思路和过程想法
(1)解题思路:
在层序遍历的基础上,将每层结点的平均值追加至结果列表。
(2)过程想法:
思路比较简单,想法比较自然。
4.4 代码
from queue import Queue
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
# 在层序遍历的基础上,将每层结点的平均值追加至结果列表。
# 用于存储结果
res = []
# 用于层序遍历的队列
myQueue = Queue()
if root:
myQueue.put(root)
while not myQueue.empty():
level = []
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
level.append(cur.val)
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
# 统计该层结点的平均值
summ = 0
for num in level:
summ += num
res.append(summ/len(level))
return res五、N叉树的层序遍历
5.1 题目
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:
输入:root = [1,null,3,2,4,null,5,6] 输出:[[1],[3,2,4],[5,6]]
示例 2:
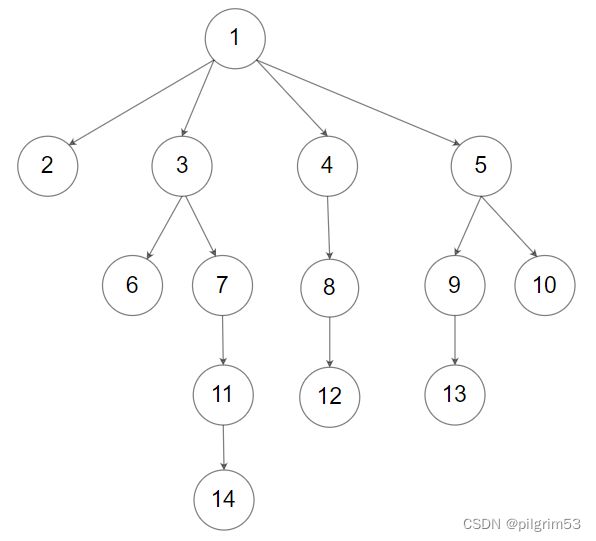
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
提示:
- 树的高度不会超过
1000 - 树的节点总数在
[0,10^4]之间
5.2 题目链接
429.N 叉树的层序遍历
5.3 解题思路和过程想法
(1)解题思路:
总体思路类似于层序遍历,只是每个结点的孩子是个数组。
(2)过程想法:
思路比较简单,想法比较自然。
5.4 代码
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
from queue import Queue
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
# 总体思路类似于层序遍历
# 用于存储结果
res = []
# 用于层序遍历的队列
myQueue = Queue()
# 层序遍历
if root:
myQueue.put(root)
while not myQueue.empty():
level = []
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
level.append(cur.val)
# 处理当前结点的所有子结点
for child in cur.children:
myQueue.put(child)
res.append(level)
return res六、在每个树行中找最大值
6.1 题目
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:
输入: root = [1,3,2,5,3,null,9] 输出: [1,3,9]
示例2:
输入: root = [1,2,3] 输出: [1,3]
提示:
- 二叉树的节点个数的范围是
[0,10^4] -2^31 <= Node.val <= 2^31 - 1
6.2 题目链接
515.在每个树行中找最大值
6.3 解题思路和过程想法
(1)解题思路:
在层序遍历的基础上,将每层结点的最大值追加至结果列表。
(2)过程想法:
思路比较简单,想法比较自然。
6.4 代码
from queue import Queue
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
# 在层序遍历的基础上,将每层结点的最大值追加至结果列表。
# 用来存储结果
res = []
# 用来层序遍历的队列
myQueue = Queue()
# 层序遍历
if root:
myQueue.put(root)
while not myQueue.empty():
level = []
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
level.append(cur.val)
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
# 求该层结点的最大值
res.append(max(level))
return res七、填充每个节点的下一个右侧节点指针
7.1 题目
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:
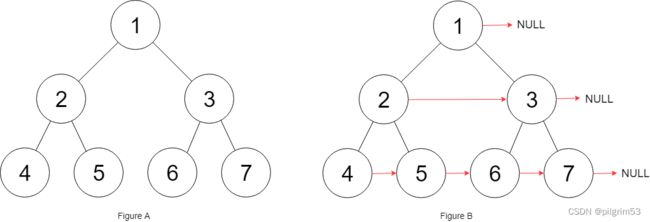
输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = [] 输出:[]
提示:
- 树中节点的数量在
[0, 2^12 - 1]范围内 -1000 <= node.val <= 1000
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
7.2 题目链接
116.填充每个节点的下一个右侧节点指针
7.3 解题思路和过程想法
(1)解题思路:
在层序遍历的过程中修改结点的next指针。因为需要在不出队元素的情况下,获取队头元素,所以此处用了deque结构。
(2)过程想法:
思路比较简单,想法比较自然。
7.4 代码
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
from collections import deque
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
# 在层序遍历的过程中修改结点的next指针。
# 用来存储结果
res = []
# 用来层序遍历的队列
myQueue = deque()
# 层序遍历
if root:
myQueue.append(root)
while len(myQueue):
size = len(myQueue)
for i in range(size):
cur = myQueue.popleft()
# 将该结点的next指针指向剩下的同层结点的队头结点
if len(myQueue):
cur.next = myQueue[0]
if cur.left:
myQueue.append(cur.left)
if cur.right:
myQueue.append(cur.right)
# 将该层最后一个结点的next指针指向None
cur.next = None
return root八、二叉树的最大深度
8.1 题目
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
提示:
- 树中节点的数量在
[0, 10^4]区间内。 -100 <= Node.val <= 100
8.2 题目链接
104.二叉树的最大深度
8.3 解题思路和过程想法
(1)解题思路:
在层序遍历的过程中统计树的层数,即树的最大高度。
(2)过程想法:
思路比较简单,想法比较自然。
8.4 代码
from queue import Queue
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
# 在层序遍历的过程中记录树的层数
# 用来存储结果
res = 0
# 用来层序遍历的队列
myQueue = Queue()
# 层序遍历
if root:
myQueue.put(root)
while not myQueue.empty():
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
# 更新树的层数
res += 1
return res九、二叉树的最小深度
9.1 题目
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
提示:
- 树中节点数的范围在
[0, 10^5]内 -1000 <= Node.val <= 1000
9.2 题目链接
111.二叉树的最小深度
9.3 解题思路和过程想法
(1)解题思路:
在层序遍历的过程中记录树的层数,最早出现的叶节点的层数就是二叉树的最小深度
(2)过程想法:
思路比较简单,想法比较自然。
9.4 代码
from queue import Queue
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
# 在层序遍历的过程中记录树的层数,最早出现的叶节点的层数就是二叉树的最小深度
# 用来存储结果
res = 0
# 用来层序遍历的队列
myQueue = Queue()
# 层序遍历
if root:
myQueue.put(root)
while not myQueue.empty():
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
# 记录叶子结点的层数
if not cur.left and not cur.right:
return res + 1
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
# 更新树的层数
res += 1
return res十、翻转二叉树
10.1 题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:
输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
10.2 题目链接
226.翻转二叉树
10.3 解题思路与过程想法
(1)解题思路:
层序遍历:翻转是基于层的翻转——左右子树进行交换,所以基于层序遍历,在遍历过程中交换左右子树。
递归:每棵树的操作都是一样的,将左右子树交换,考虑使用递归。1. 主要步骤——当前左右子树交换,左子树内部完成交换,右子树内部完成交换。2. 出口——当前树的根节点为空结点。3. 递归的传入值与返回值——传入指向根结点的指针,在函数内部修改root结点的属性(左右指针)。
迭代:可以递归实现的,也可以用栈实现----迭代。此处以前序遍历举例;但需注意:若是借助中序遍历可能出现重复反转
(2)过程想法:
思路比较简单,想法比较自然。
10.4 代码
10.4.1 层序遍历
from queue import Queue
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 翻转是基于层的翻转,即左右子树进行交换,所以基于层序遍历,在遍历过程中交换左右子树
# 用于层序遍历的队列
myQueue = Queue()
# 层序遍历
if root:
myQueue.put(root)
while not myQueue.empty():
size = myQueue.qsize()
for i in range(size):
cur = myQueue.get()
# 无论左右子树是否有空树,直接交换指针内容
cur.left,cur.right = cur.right,cur.left
if cur.left:
myQueue.put(cur.left)
if cur.right:
myQueue.put(cur.right)
return root10.4.2 递归
class Solution:
def inverse(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 主要步骤:当前左右子树交换,左子树内部完成交换,右子树内部完成交换。
# 出口为:当前树的根节点为空结点
if root:
root.left,root.right = root.right,root.left
self.inverse(root.left)
self.inverse(root.right)
else:
return
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 每棵树的操作都是一样的,将左右子树交换,考虑使用递归
self.inverse(root)
return root10.4.3 前序迭代
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 可以递归实现的,也可以用栈实现----迭代
# 此处以前序遍历举例;但需注意:若是借助中序遍历可能出现重复反转
mystack = []
# 前序遍历:根左右----栈:右左根
if root:
mystack.append(root)
while len(mystack):
cur = mystack.pop()
# 交换左右子树
cur.left,cur.right = cur.right,cur.left
if cur.right:
mystack.append(cur.right)
if cur.left:
mystack.append(cur.left)
return root十一、对称二叉树
11.1 题目
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
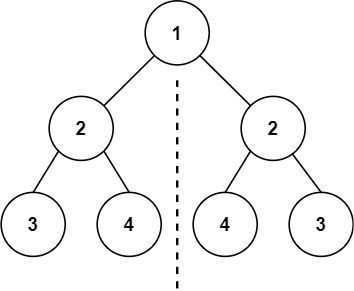
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
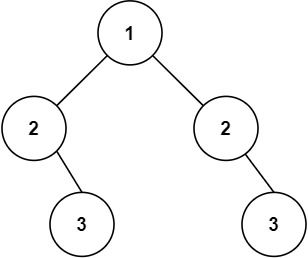
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
11.2 题目链接
101.对称二叉树
11.3 解题思路与过程想法
(1)解题思路:
判断树是否具有镜像对称的特性,而树的结构具有相似性,考虑使用递归。1)主体思路:判断树的“内侧”和“外侧”是否相等。2)最终出口:判断两结点是否相等。3)递归函数的传入值与返回值:指向左右子树的指针,两子树是否具有镜像特性的结果。
(2)过程想法:
最初只想到判断左右孩子是否相等,但是又觉得不对,没想到如何去写主体部分。
11.4 代码
class Solution:
def symm(self,left,right) -> bool:
# 若有一方为空,则直接返回结果False
if not left and right:
return False
# 若有一方为空,则直接返回结果False
elif left and not right:
return False
# 若两方为空,则直接返回结果True
elif not left and not right:
return True
# 若两方数值不同,则直接返回结果False
elif left.val != right.val:
return False
else:
# 比较内侧与外侧是否相等----即两边是否符合镜像对称
inside = self.symm(left.right,right.left)
outside = self.symm(left.left,right.right)
return inside and outside
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
# 判断树是否具有镜像对称的特性,而树的结构具有相似性,考虑使用递归
# 主体思路:判断树的“内侧”和“外侧”是否相等
# 最终出口:判断两结点是否相等
# 递归函数的传入值与返回值:指向左右子树的指针,两子树是否具有镜像特性的结果
if not root:
return True
else:
return self.symm(root.left,root.right)