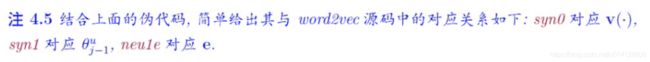基于Hierarchical Softmax的模型
本节开始正式介绍word2vec中用到的两个重要模型——CBOW模型（Continuous Bag-of-Words ）和Skip-gram模型（Continuous Skip-gram）。
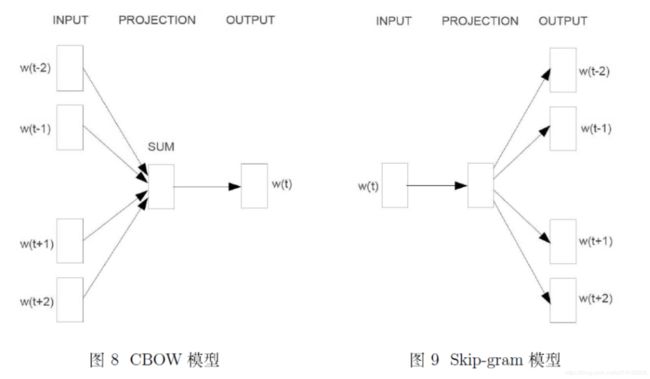
由图8、9可见，两个模型都包含三层：输入层、投影层和输出层。
CBOW是在已知当前词 w t w_{t} wt的上下文 w t − 2 , w t − 1 , w t + 1 , w t + 2 w_{t-2}, w_{t-1}, w_{t+1}, w_{t+2} wt−2,wt−1,wt+1,wt+2的前提下预测当前词 w t w_{t} wt。
Skip-gram则相反，是在已知当前词 w t w_{t} wt的前提下，预测其上下文 w t − 2 , w t − 1 , w t + 1 , w t + 2 w_{t-2}, w_{t-1}, w_{t+1}, w_{t+2} wt−2,wt−1,wt+1,wt+2。
对于CBOW和Skip-gram两个模型，word2vec给出了两套框架，他们分别基于Hierarchical Softmax和Negative Sampling来进行设计。即，当前word2vec主流实现有4种：基于Negative Sampling框架和基于Hierarchical Softmax框架的CBOW模型和Skip-gram模型。
在word2vec(2) 背景知识中，介绍了目标函数为如下对数似然函数，然后对这个函数进行最大化。
神经网络中已经给定了一种构造方式：
对于基于Hierarchical Softmax 的CBOW，优化目标函数形如公式4.1。
而基于Hierarchical Softmax 的CBOW，目标函数形如：
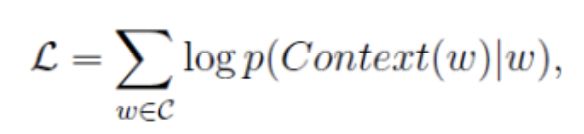
优化过程中的重心在 p ( w ∣ c o n t e x t ( w ) ) p(w|context(w)) p(w∣context(w))， p ( c o n t e x t ( w ) ∣ w ) p(context(w)|w) p(context(w)∣w)的构造上。注意，对一个样本而言， ( w , c o n t e x t ( w ) ) (w,context(w)) (w,context(w))表示skip-gram是根据中间词去预测上下文， ( w , c o n t e x t ( w ) ) (w,context(w)) (w,context(w))表示CBOW的样本，是根据上下文去预测中间词。
5.1 CBOW模型
5.1.1 CBOW网络结构
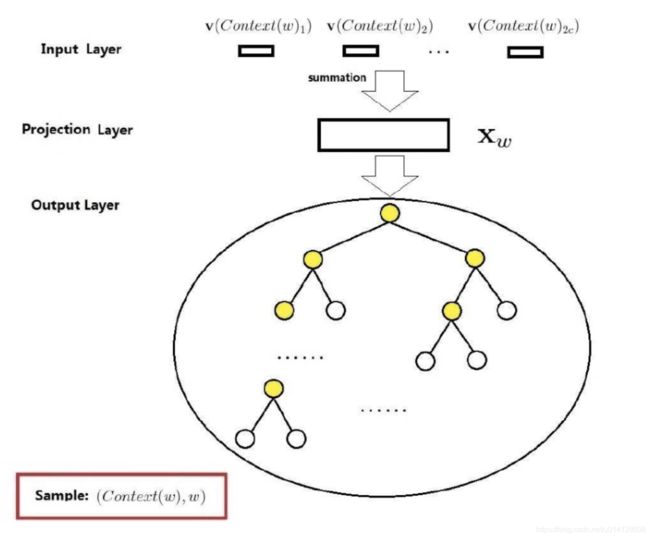
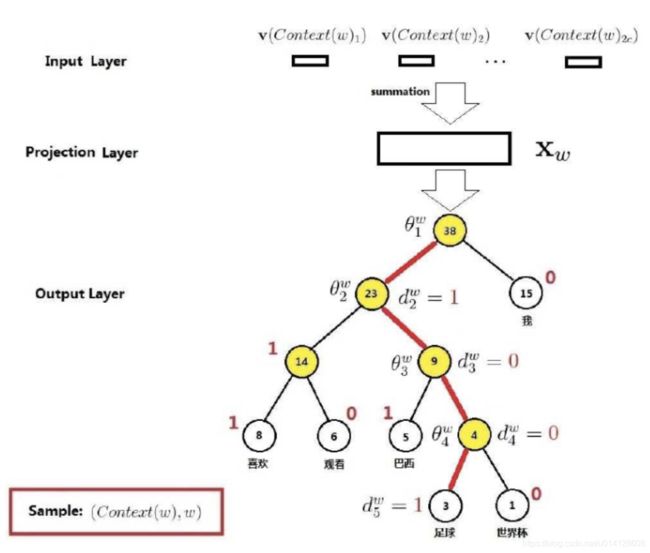
下图给出了基于层次Softmax的CBOW的整体结构，首先它包括输入层、投影层和输出层：
- 输入层：包含 c o n t e x t ( w ) context(w) context(w)中2c个词的词向量 v ( c o n t e x t ( w ) 1 ) , v ( c o n t e x t ( w ) 2 ) , , . . . , v ( c o n t e x t ( w ) 2 c ) ∈ R m v(context(w)_{1}),v(context(w)_{2}),,...,v(context(w)_{2c})\in \mathbb{R}^{m} v(context(w)1),v(context(w)2),,...,v(context(w)2c)∈Rm，这里m表示词向量的长度。
- 投影层：将输入层的2c个向量求和累加（ 大师，这里为啥要求和累加啊 ），公式如下：
- 输出层：输出层对应一棵二叉树，它是以语料中出现过的词当叶子结点，以各词在语料中出现的次数当权值构造出的Huffman树。在这颗哈夫曼树中，叶节点有N(=|D|)个，分别对应词典D中的词。
对比以往的神经概率语言模型和CBOW模型主要有以下三种不同：
- 从输入层到投影层的操作：前者是通过首尾相连的拼接，后者是通过累加求和。
- 隐藏层：前者有隐藏层，后者无隐藏层
- 输出层：前者是线性结构，后者是树形结构
在神经概率语言模型中，模型的大部分计算集中在隐藏层和输出层之间的矩阵向量运算，以及输出层上的softmax 归一化运算。而从上面的对比中可见，CBOW 模型对这些计算复杂度高的地方有针对性地进行了改变，首先，去掉了隐藏层，其次，输出层改用了Huffiman 树，从而为利用Hierarchical softmax 技术奠定了基础。
##5.1.2 梯度计算
Hierarchical Softmax是word2vec中用于提高性能的一项关键技术。为了描述方便，引入若干符号。考虑到Huffman树种的某个叶子结点，假设对应词典D中的词w，记：
- p w p^w pw：从根结点出发到达 w w w对应的叶子结点的路径。
- l w l^w lw：路径 p w p^w pw中包含的结点的个数。（包含根节点和叶子节点）
- p 1 w , p 2 w , . . . , p l w w p_{1}^{w},p_{2}^{w},...,p_{l^{^{w}}}^{w} p1w,p2w,...,plww：路径 p w p^w pw中的 l w l^w lw个结点，其中 p 1 w p_{1}^{w} p1w表示根节点， p l w w p_{l^{^{w}}}^{w} plww表示词 w w w对应的结点。
表示词 w w w的Huffman编码，是由 l w − 1 l^w-1 lw−1位编码构成的， d j w d_{j}^{w} djw表示路径 p w p^w pw中的第j个单词对应的哈夫曼编码，根结点不参与对应的编码。（所以d的下标是从2开始的。）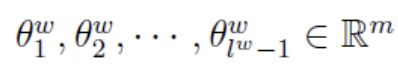
θ j w \theta_{j}^{w} θjw表示路径 p w p^w pw中第j个非叶子节点对应的词向量。之所以给非叶子节点定义词向量，是因为这里的非叶子节点的词向量会作为下面的一个辅助变量进行计算，在下面推导公式的时候就会发现它的作用了。
既然已经引入了那么多符号，我们通过一个简单的例子把它们落到实处吧，我们考虑单词 w w w="足球"的情形。
下图中红色线路就是我们的单词走过的路径，整个路径上的5个结点就构成了路径 p w p^w pw ，其长度 l w = 5 l^w=5 lw=5 ，然后 p 1 w , p 2 w , . . . , p 5 w p_{1}^{w},p_{2}^{w},...,p_{5}^{w} p1w,p2w,...,p5w就是路径 p w p^w pw上的五个结点，其中 p 1 w p_{1}^{w} p1w 对应根结点。 d 2 w , d 3 w , d 4 w , d 5 w d_{2}^{w},d_{3}^{w},d_{4}^{w},d_{5}^{w} d2w,d3w,d4w,d5w 分别为1,0,0,1，即"足球"对应的哈夫曼编码就是1001。最后 θ 1 w , θ 2 w , θ 3 w , θ 4 w \theta_{1}^{w},\theta_{2}^{w},\theta_{3}^{w},\theta_{4}^{w} θ1w,θ2w,θ3w,θ4w就是路径 p w p^w pw 上的4个非叶子节点对应的向量。
下面我们需要开始考虑如何构建条件概率函数 p ( w ∣ c o n t e x t ( w ) ) p(w|context(w)) p(w∣context(w)) ，更具体地说，就是如何利用向量 x w ∈ R m x_{w} \in \mathbb{R}^{m} xw∈Rm 以及huffman树来定义函数 p ( w ∣ c o n t e x t ( w ) ) p(w|context(w)) p(w∣context(w))呢？
以上面的w="足球"为例，从根节点到"足球"这个叶子节点，经历了4次分支，也就是那4条红色的线，而对于这个哈夫曼树而言，每次分支相当于一个二分类。
既然是二分类，那么我们可以定义一个为正类，一个为负类。我们的"足球"的哈夫曼编码为1001，这个哈夫曼编码是不包含根节点的，因为根节点没法分为左还是右子树（这里限定了左为1，右为0，但是根节点无法分别，指的是当前节点没有父节点，不能归为左子树或者右子数，不是说当前节点没有左子树或右子数）。那么根据哈夫曼编码，我们一般可以把正类就认为是哈夫曼编码里面的1，而负类认为是哈夫曼编码里面的0。不过这只是一个约定而已，因为哈夫曼编码和正类负类之间并没有什么明确要求对应的关系。事实上，**Word2Vec将编码为1的认定为负类，而编码为0的认定为正类，也就是说如果分到了左子树，就是负类；分到了右子树，就是正类。**为了方便对照着文档看源码，下文中统一采用后者，即约定。
即编码是1的时候，label = 0，是负例。简而言之，就是将一个结点进行分类时，分到左边就是负类，分到右边就是正类。
在进行二分类的时候，这里选择了Sigmoid函数。那么，一个结点被分为正类的概率就是：
被分为负类的概率就是：
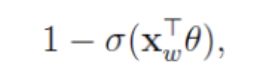
注意，公式里面包含的有 θ \theta θ，这个就是非叶子对应的向量 θ j w \theta_{j}^{w} θjw。
对于从根节点出发到达“足球”这个叶子节点所经历的4次二分类，将每次分类的概率（条件概率）写出来就是：
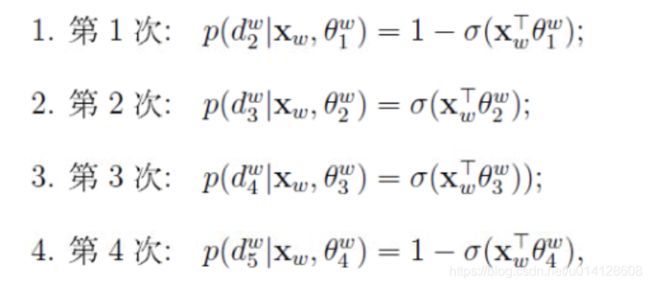
但是，我们要求的是 p ( w ∣ c o n t e x t ( w ) ) p(w|context(w)) p(w∣context(w))，即 p ( 足 球 ∣ c o n t e x t ( 足 球 ) ) p(足球|context(足球)) p(足球∣context(足球)) ，它跟这4个概率值有什么关系呢？关系就是：
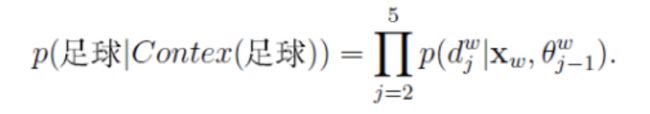
至此，通过w="足球"的小例子，Hierarchical Softmax的基本思想就已经介绍完了。小结一下：对于词典中的任意一个单词 w w w ，哈夫曼树中肯定存在一条从根节点到单词 w w w对应叶子结点的路径 p w p^w pw ，且这条路径是唯一的。路径 p w p^w pw 上存在 l w − 1 l^w-1 lw−1个分支，将每个分支看做一次二分类，每一次分类就产生一个概率，将这些概率乘起来，就是所需要的 p ( w ∣ c o n t e x t ( w ) ) p(w|context(w)) p(w∣context(w))。
条件概率 p ( w ∣ c o n t e x t ( w ) ) p(w|context(w)) p(w∣context(w))的一般公式可写为：
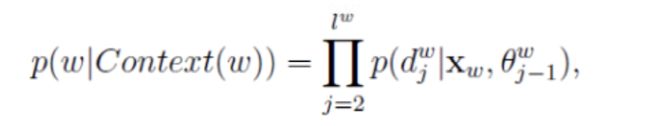
其中：
或者写成整体表达式：
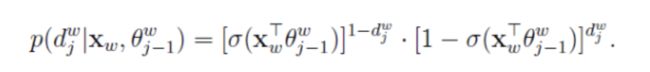
将上式代入对数似然函数。
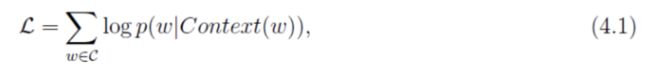
（ 注，这里的x表示输入层的2c个向量求和累加 ）
为下面梯度推导方便起见，将上式中双重求和符号下花括号里的内容简记为：
以上就是CBOW模型的目标函数。接下来将讨论如何将这个函数最大化。在word2vec中，由于使用的是随机梯度上升法。
随机梯度上升法的做法是：每取一个样本 ( c o n t e x t ( w ) , w ) (context(w), w) (context(w),w)就对目标函数中所有（相关的）参数做一次刷新。观察目标函数易知，该函数中的参数包括向量 x w , θ j − 1 w , w ∈ C , j = 2 , . . . , l w x_{w},\theta_{j-1}^{w},w\in C,j=2,...,l^w xw,θj−1w,w∈C,j=2,...,lw，为此，先给出函数 L ( w , j ) L(w,j) L(w,j)关于这些向量的梯度。
于是， θ j − 1 w \theta_{j-1}^{w} θj−1w的更新公式可写为：
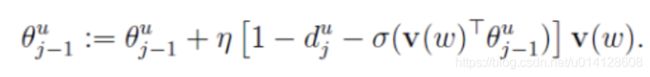
接下来考虑 L ( w , u , j ) L(w,u,j) L(w,u,j)关于 v ( w ) v(w) v(w)的梯度。同样利用 L ( w , u , j ) L(w,u,j) L(w,u,j)中 v ( w ) v(w) v(w)和 θ j − 1 w \theta_{j-1}^{w} θj−1w的对称性，有
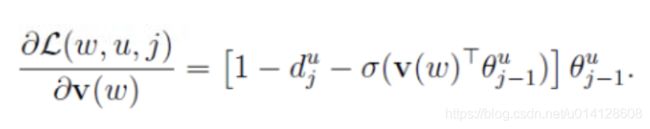
于是， v ( w ) v(w) v(w)的更新公式可写为：
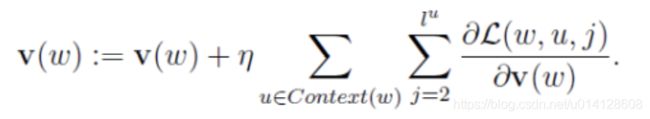
下面以样本 ( w , c o n t e x t ( w ) ) (w,context(w)) (w,context(w))为例，给出skip-gram模型中采用随机梯度上升法更新各参数的伪代码。
word2vec 代码中，并不是等 C o n t e x t ( w ) Context(w) Context(w) 中的所有词都处理完后才更新 v ( w ) v(w) v(w)，而是每处理完 C o n t e x t ( w ) Context(w) Context(w)中的一个词 u u u，就及时更新一次 v ( w ) v(w) v(w)。
同样，需要注意的是，循环体内的步骤3和步骤4不能次序交换，即 θ j − 1 w \theta_{j-1}^{w} θj−1w要等贡献到 e e e后才更新。
①
②(隐藏层)
③(输出层)
红色
绿色
- [Word2Vec] Efficient Estimation of Word Representations in Vector Space (Google 2013)
Google的Tomas Mikolov提出word2vec的两篇文章之一，这篇文章更具有综述性质，列举了NNLM、RNNLM等诸多词向量模型，但最重要的还是提出了CBOW和Skip-gram两种word2vec的模型结构。虽然词向量的研究早已有之，但不得不说还是Google的word2vec的提出让词向量重归主流，拉开了整个embedding技术发展的序幕。
- [Word2Vec] Distributed Representations of Words and Phrases and their Compositionality (Google 2013)
Tomas Mikolov的另一篇word2vec奠基性的文章。相比上一篇的综述，本文更详细的阐述了Skip-gram模型的细节，包括模型的具体形式和 Hierarchical Softmax和 Negative Sampling两种可行的训练方法。
- [Word2Vec] Word2vec Parameter Learning Explained (UMich 2016)
虽然Mikolov的两篇代表作标志的word2vec的诞生，但其中忽略了大量技术细节，如果希望完全读懂word2vec的原理和实现方法，比如词向量具体如何抽取，具体的训练过程等，强烈建议大家阅读UMich Xin Rong博士的这篇针对word2vec的解释性文章。惋惜的是Xin Rong博士在完成这篇文章后的第二年就由于飞机事故逝世，在此也致敬并缅怀一下Xin Rong博士。
—————————————————————————————————————
介绍Word2vec之前，首先说明一下，什么是embedding?
embedding就是用低维向量表征一个对象。这个对象可以是一个词，或是一个商品，或是一个电影等等。embedding具有如下性质：
- 距离相近的embedding向量对应的物体有相近的含义。比如 embedding(复仇者联盟)和embedding(钢铁侠)之间的距离就会很接近，但 embedding(复仇者联盟)和embedding(乱世佳人)的距离就会远一些。
- embedding甚至还具有数学运算的关系。比如embedding（纽约）- embedding（美国）+ embedding(法国) ≈ Embedding(巴黎)
从embedding的特性来看，能够用低维向量对物体进行编码还能保留其含义的特点非常适合深度学习。
在传统机器学习模型构建过程中，我们经常使用one hot encoding对离散特征，特别是id类特征进行编码，但由于one hot encoding的维度等于物体的总数，比如阿里的商品one hot encoding的维度就至少是千万量级的。这样的编码方式对于商品来说是极端稀疏的。而深度学习的特点以及工程方面的原因使其不利于稀疏特征向量的处理。因此如果能把物体编码为一个低维稠密向量再喂给DNN，自然是一个高效的基本操作。
因此在推荐系统中，embedding 的应用之一是实现高维稀疏特征向量向低维稠密特征向量的转换，将训练好的embedding可以当作输入深度学习模型的特征。
对word的vector表达的研究早已有之，但让embedding方法空前流行，我们还是要归功于google的word2vec。不过，在说Word Embedding之前，先更粗略地介绍下语言模型，因为一般NLP里面做预训练一般的选择是用语言模型任务来做。
什么是语言模型？看上图就明白了，为了能够量化地衡量哪个句子更像一句人话，可以设计如上图所示函数，核心函数P的思想是根据句子里面前面的一系列前导单词预测后面跟哪个单词的概率大小（理论上除了上文之外，也可以引入单词的下文联合起来预测单词出现概率）。句子里面每个单词都有个根据上文预测自己的过程，把所有这些单词的产生概率乘起来，数值越大代表这越像一句人话。
简而言之，语言模型，即设计一个函数，根据上文预测后面跟随单词的概率大小。
NNLM
假设现在需要设计一个神经网络结构，去实现这个语言模型的任务，目前有很多语料做这个事情，用来训练一个神经网络。在训练好网络之后，假设输入一句话的前面几个单词，要求这个网络输出后面紧跟的单词应该是哪个，应该如何实现呢？
具体的实现流程如上图所示，图中的网络结构，这其实就是大名鼎鼎的中文人称“神经网络语言模型（Nerual Network Language Model）”，英文小名NNLM的网络结构，用来做语言模型。这个工作有年头了，是个陈年老工作，是Bengio 在2003年发表在JMLR上的论文。
NNLM的学习任务是输入某个句中单词 W t W_{t} Wt（假设这个单词是"Bert"）前面句子的 t − 1 t-1 t−1个单词，要求网络正确预测单词W_{t}，即最大化：
P ( W t = B e r t ∣ W 1 , W 2 , . . . , W t − 1 ; θ ) P(W_{t} = Bert| W_{1},W_{2},...,W_{t-1};\theta ) P(Wt=Bert∣W1,W2,...,Wt−1;θ)
在NNLM中，前面任意单词 W i W_{i} Wi用Onehot编码（比如：0001000）作为原始单词输入，之后乘以矩阵Q后获得向量 C ( W i ) C(W_{i}) C(Wi)，每个单词的 C ( W i ) C(W_{i}) C(Wi)进行拼接（ 这里的拼接可以有很多种方式 ），随后接入隐藏层，然后接softmax去预测后面应该后续接哪个单词。
图中， C ( W i ) C(W_{i}) C(Wi)其实就是单词对应的Word Embedding值，那个矩阵Q包含V行，V代表词典大小，每一行内容代表对应单词的Word embedding值。只不过Q的内容也是网络参数，需要学习获得，训练刚开始用随机值初始化矩阵Q，当这个网络训练好之后，矩阵Q的内容被正确赋值，每一行代表一个单词对应的Word embedding值。（ 原始单词是[1, V]的向量，Q是大小为[V, m]的矩阵，二者相乘，相当于选中了矩阵Q的1行，即原始单词one-hot后不为0的那一行，此时生成该单词对应的Word embedding值。）所以你看，通过这个网络学习语言模型任务，这个网络不仅自己能够根据上文预测后接单词是什么，同时获得一个副产品，就是那个矩阵Q，这就是单词的Word Embedding是被如何学会的。
word2vec
2013年最火的用语言模型做Word Embedding的工具是Word2Vec，后来又出了Glove，Word2Vec是怎么工作的呢？如下图所示：
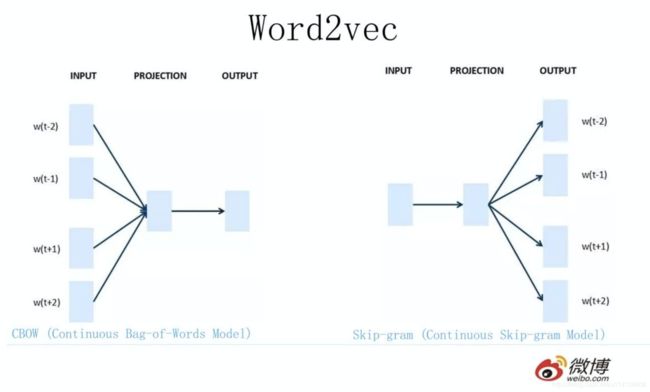
2013年，Google开源了一款用于词向量计算的工具——word2vec，引起了工业界和学术界的关注。首先，word2vec可以在百万数量级的词典和上亿的数据集上进行高效地训练；其次，该工具得到的训练结果——词向量（word embedding），可以很好地度量词与词之间的相似性。随着深度学习（Deep Learning）在自然语言处理中应用的普及，很多人误以为word2vec是一种深度学习算法。其实word2vec算法的背后是一个浅层神经网络。另外需要强调的一点是，word2vec是一个计算word vector的开源工具。当我们在说word2vec算法或模型的时候，其实指的是其背后用于计算word vector的CBoW模型和Skip-gram模型。很多人以为word2vec指的是一个算法或模型，这也是一种谬误。
Word2Vec的网络结构其实和NNLM是基本类似的，区别是二者训练方法不太一样。Word2Vec有两种训练方法， 一种叫CBOW，核心思想是在一个句子里面把一个词抠掉，用这个词的上文和下文去预测被抠掉的这个词；第二种叫做Skip-gram，和CBOW正好反过来，输入某个单词，要求网络预测它的上下文单词。
反观NNLM是怎么训练的呢？是输入一个单词的上文，去预测这个单词。这是有显著差异的。为什么Word2Vec这么处理？原因很简单，因为Word2Vec和NNLM不一样，NNLM的主要任务是要学习一个解决语言模型任务的网络结构，语言模型就是要看到上文预测下文，在NNLM中，word embedding只是无心插柳的一个副产品（ 这里学到的word embedding有些类似于DNN的参数矩阵 W W W）。但是Word2Vec目标不一样，它单纯就是要word embedding的，这是主产品，所以它完全可以随性地这么去训练网络。
在word2vec中，采用了标准的预训练过程。要理解这一点要看看学会Word Embedding后下游任务是怎么用它的。
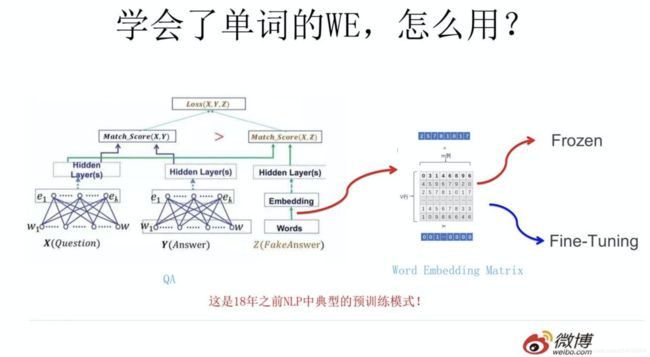
假设如上图所示，我们有个NLP的下游任务，比如QA，就是问答问题，所谓问答问题，指的是给定一个问题X，给定另外一个句子Y，要判断句子Y是否是问题X的正确答案。问答问题假设设计的网络结构如上图所示，这里不展开讲了，懂得自然懂，不懂的也没关系，因为这点对于本文主旨来说不关键，关键是网络如何使用训练好的Word Embedding的。它的使用方法其实和前面讲的NNLM是一样的，句子中每个单词以Onehot形式作为输入，然后乘以学好的Word Embedding矩阵Q，就直接取出单词对应的Word Embedding了。这乍看上去好像是个查表操作，不像是预训练的做法是吧？其实不然，那个Word Embedding矩阵Q其实就是网络Onehot层到embedding层映射的网络参数矩阵。所以你看到了，使用Word Embedding等价于什么？等价于把Onehot层到embedding层的网络用预训练好的参数矩阵Q初始化了。这跟图像领域的低层预训练过程其实是一样的，区别无非Word Embedding只能初始化第一层网络参数，再高层的参数就无能为力了。下游NLP任务在使用Word Embedding的时候也类似图像有两种做法，一种是Frozen，就是Word Embedding那层网络参数固定不动；另外一种是Fine-Tuning，就是Word Embedding这层参数使用新的训练集合训练也需要跟着训练过程更新掉。
在下游任务中，one-hot到embedding间的网络参数矩阵的初始化，不是随机初始化了，而是用训练好的word embedding。
Word Embedding其实对于很多下游NLP任务是有帮助的，但实际效果并没有想象中好，主要原因在于word2vec有问题。这片在Word Embedding头上笼罩了好几年的乌云是什么？是多义词问题。如下图所示：
多义词对Word Embedding来说有什么负面影响？如上图所示，比如多义词Bank，有两个常用含义，但是Word Embedding在对bank这个单词进行编码的时候，是区分不开这两个含义的，因为它们尽管上下文环境中出现的单词不同，但是在用语言模型训练的时候，不论什么上下文的句子经过word2vec，都是预测相同的单词bank，而同一个单词占的是同一行的参数空间，这导致两种不同的上下文信息都会编码到相同的word embedding空间里去。所以word embedding无法区分多义词的不同语义，这就是它的一个比较严重的问题。
#Q & A
1.为什么深度学习不利于稀疏特征向量的处理？
因为深度学习表达能力强，特征过于稀疏的可能造成过拟合。从模型角度来讲，特征过于稀疏会导致整个网络收敛过慢，因为每次更新只有极少数的权重会得到更新。这在样本有限的情况下几乎会导致模型不收敛。
#参考链接
- 万物皆Embedding，从经典的word2vec到深度学习基本操作item2vec
#参考链接 - 什么是embedding
- embedding的特性与应用
- NNLM的原理