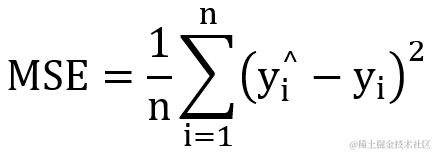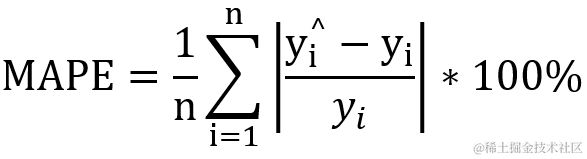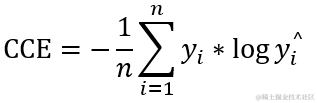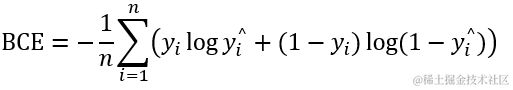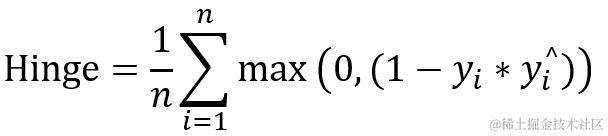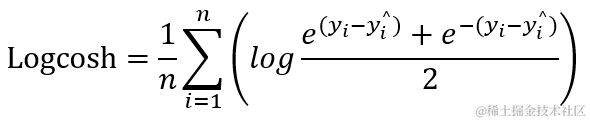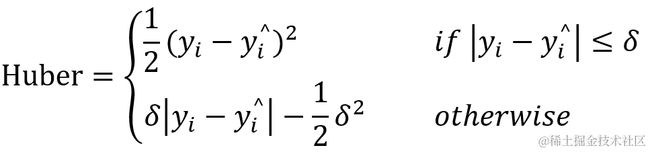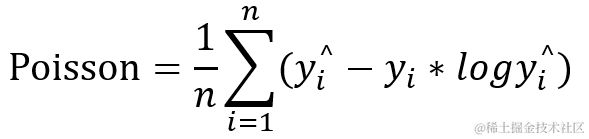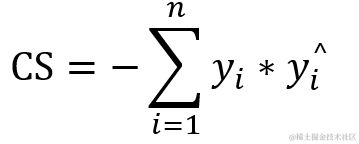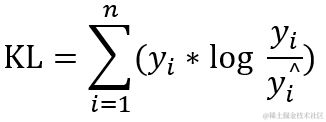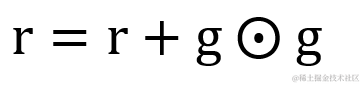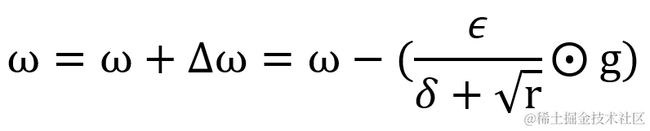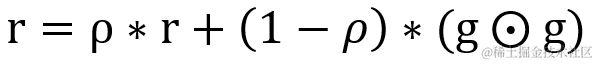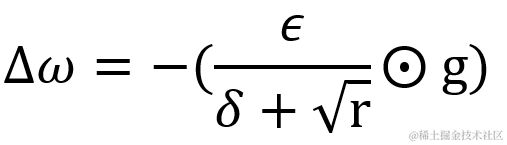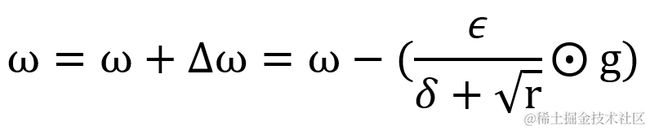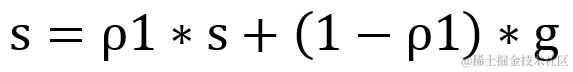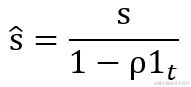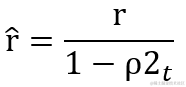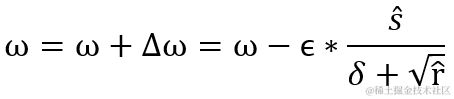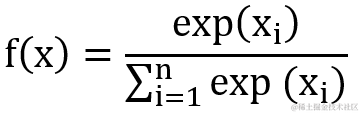TensorFlow 2.0 深度学习实战 —— 详细介绍损失函数、优化器、激活函数、多层感知机的实现原理

AI 人工智能包含了机器学习与深度学习，在前几篇文章曾经介绍过机器学习的基础知识，包括了监督学习和无监督学习，有兴趣的朋友可以阅读《 [Python 机器学习实战]》。
而深度学习开始只是机器学习的一分支领域，它更强调从连续的层中进行学习，这种层级结构中的每一层代表不同程序的抽象，层级越高，抽象程度越大。这些层主要通过神经网络的模型学习得到的，最大的模型会有上百层之多。而最简单的神经网络分为输入层，中间层（中间层往往会包含多个隐藏层），输出层。
下面几篇文章将分别从前馈神经网络 FNN、卷积神经网络 CNN、循环神经网络 RNN、编码器等领域进行详细介绍。

一、深度学习简介

1.1 深度学习的起源

AI 人工智能包含了机器学习，而深度学习本属于机器学习的一个分支，它结合了生物神经学的原理，以多层学习模型，将数据层层细化提炼，最后完成输出。如今深度学习已经广泛应用于图像识别、人脸识别、语音识别、搜索引擎、自动驾驶等多个领域。

深度学习强调从连续的层中进行学习，每个层都是通过神经网络的模型来学习得到，神经网络的结构逐层叠加，最后通过输出层完成输出。深度学习的原理本来源于生物神经学，由于受到外界刺激神经元细胞发送信号，从其他神经元接收，多层叠加后形成树状结构，当到某个阈值后转换成激活状态。而深度学习的结构与此类似，原始数据输入后会经过多个隐藏层，每个隐藏层都会存在若干个神经元，最后通过输出层完成输出，层越深所提炼到纯度越高。

1.2 深度学习的工作原理

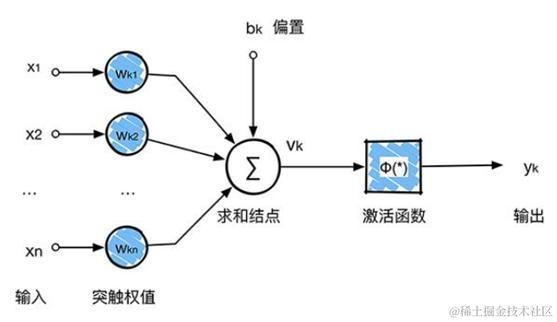
打个比方在输入层有 n 个参数 X1，X2，…，Xn，每个参数的取值权重都保存在W1，W2，…，Wn，偏置量都保存于 h1，h2，…，hn，其求和结点值为公式

当结点值超过某个值时就会引发激活函数 Φ(*) 把数据输出到下一层，周而复始直到输出层。而深度学习的意义在于通过千万个监督数据不断重复学习，从而调整权重与偏置量，使其与监督数据匹配。完成学习后，即使有末经测试的新数据输入，系统也可根据原有的基础进行判断，不断地完善。
区别于传统的数据学习，深度学习的不同在于： 1. 深度学习强调了模型结构的深度，它最少的深度有3层，就是输入层，隐藏层，输出层，而通常会有5层、6层，甚至10多层的隐藏层； 2. 深度明确了特征学习的重要性，通过逐层特征变换，将样本在原空间的特征表示变换到一个新特征空间，从而使特征纯度越来越高，让分类或预测更容易。

1.3 Tensorflow 2.0 简介

用于实现深度学习的框架有很多，常用的有 Tensorflow、Theano、CNTK 等，而在 Tensorflow 1.x 前 Keras 是用 Python 开发的模型库，能兼顾三大平台，在不同的后端运行。当 Tensorflow 2.0 出现后，已经把 Keras 定义为训练模型的一个 API 规范，把它包含到 Tensorflow 2.0 的一个库里，此后使用 Keras 时无需再额外下载 Keras 包。Eager 执行模型也是 Tensorflow 2.0 的一个重要特征，它可以跟 Keras 结合使用，形成一个高性能的流水线执行模式。另外 Tensorflow 2.0 使用函数代替了原来的 session 会话模式，把设计重心放在 Eager 执行模型上。以后在设计模型时无需要再考虑全局变量，占位符 placeholder 等繁琐的细节。Tensorflow 2.0 的应用将在下面几篇文章中一一介绍，敬请留意。

二、损失函数

上一节介绍到，深度学习是通过大量的监督数据进行训练，计算损失函数的最小值从而得出最符合现状的权重与偏移量的。损失函数的公式有很多，最常用的就是均方误差和交叉熵误差两种，关于损失函数的原理在《 [Python机器学习实战 —— 监督学习]》中已经深入讲解过，在这章中主要从实用层面进行介绍。

在 Tensoflow 2.0 中可通过 model.compile (optimizer , loss , metrics)  方法绑定损失函数和计算梯度的方法，loss 参数可绑定 tensorflow.keras.losses 中多种已定义的损失函数，常用的 loss 损失函数有下面几种：（当中 yi 为真实值 yi^为预测值）

2.1 mean_squared_error 均方误差

1 def mean_squared_error(y_true, y_pred):
2     return K.mean(K.square(y_pred - y_true), axis=-1)

均方误差是最常用的损失函数，一般用于回归计算

2.2 mean_absolute_error 平均绝对误差

1 def mean_absolute_error(y_true, y_pred):
2     return K.mean(K.abs(y_pred - y_true), axis=-1)

平均绝对误差与均方误差类似，一般用于回归计算，只不过均方误差公式使用的是平方和的平均值，而平均绝对误差则是用绝对值的平均值

2.3 mean_absolute_percentage_error 平均绝对值百分比误差

1 def mean_absolute_percentage_error(y_true, y_pred):
2     diff = K.abs((y_true - y_pred) / K.clip(K.abs(y_true),
3                                             K.epsilon(),
4                                             None))
5     return 100. * K.mean(diff, axis=-1)

平均绝对值百分比误差则是用真实值与预测值的差值比例进行计算的，通常会乘以百分比进行计算，一般用于回归计算。这是销量预测最常用的指标，在实际的线上线下销量预测中有着非常重要的评估意义

2.4 mean_squared_logarithmic_error 对数方差

1 def mean_squared_logarithmic_error(y_true, y_pred):
2     first_log = K.log(K.clip(y_pred, K.epsilon(), None) + 1.)
3     second_log = K.log(K.clip(y_true, K.epsilon(), None) + 1.)
4     return K.mean(K.square(first_log - second_log), axis=-1)

对数方差计算了一个对应平方对数（二次）误差或损失的预估值风险度量，一般用于回归计算。当目标具有指数增长的趋势时, 该指标最适合使用, 例如人口数量, 跨年度商品的平均销售额等。

2.5 categorical_crossentropy 多类交叉熵

1 def categorical_crossentropy(y_true, y_pred):
2     return K.categorical_crossentropy(y_true, y_pred)

交叉熵主要用于分类算法，当使用交叉熵损失函数时，目标值应该是分类格式 (nb_samples, nb_classes)  (即如果有10个类，输出数据格式应为 [-1,10]，每个样本的目标值 nb_class 应该是一个10维的向量 ，这个向量除了表示类别的那个索引为1，其他均为0，类似于 [ [0,0,0,0,1,0,0,0,0,0],[0,1,0,0,0,0,0,0,0,0] , […] … ] 数组)。 为了将 整数目标值转换为分类目标值，可以使用 Keras 实用函数 to_categorical(int_labels, num_classes=None)

2.6  sparse_categorical_crossentropy 稀疏交叉熵

1 def sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=-1):
2     y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred)
3     y_true = math_ops.cast(y_true, y_pred.dtype)
4     return backend.sparse_categorical_crossentropy(
5         y_true, y_pred, from_logits=from_logits, axis=axis)

SCCE 稀疏多分类交叉熵与 CCE 多分类交叉熵的实现方式相类似，主要用于分类算法，只是目标值输出值格式略有不同，CEE以向量作为输出，而SCEE 则直接转化为索引值进行输出。例如同一组测试数据如果有10个分类CEE 的输出方式是 [-1，10]，类似于 [ [0,0,0,0,1,0,0,0,0,0],[0,1,0,0,0,0,0,0,0,0] , […] … ] 数组)。而SCCE的输出方式将会是[-1,1]，即类似 [ [1]，[3]，[4]，[9] … ] 类型的数组。

2.7 binary_crossentropy 二进制交叉熵

def binary_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0):
     y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred)
  　　y_true = math_ops.cast(y_true, y_pred.dtype)
  　　label_smoothing = ops.convert_to_tensor_v2_with_dispatch(
      　　label_smoothing, dtype=backend.floatx())

  　　def _smooth_labels():
    　　return y_true * (1.0 - label_smoothing) + 0.5 * label_smoothing

  　　y_true = smart_cond.smart_cond(label_smoothing, _smooth_labels,
                                 lambda: y_true)
  　　return backend.mean(
     　　 backend.binary_crossentropy(
         　　 y_true, y_pred, from_logits=from_logits), axis=-1)

CCE 和 SCCE 主要用于多分类, 而 BCE 更适用于二分类，由于CCE 需要输出 n_class 个通道而 BCE 只需要输出一条通道，所以同一组测试数据往往 BCE 的运行效率会更高。需要注意的是，如果使用BCE损失函数，则节点的输出应介于(0-1)之间，这意味着你必须在最终输出中使用sigmoid激活函数。

2.8 hinge 合页

1 def hinge(y_true, y_pred):
2     return K.mean(K.maximum(1. - y_true * y_pred, 0.), axis=-1)

它通常用于 “maximum-margin” 二分类任务中，如 SVM 支持向量机。由公式可以看出，使用 hinge 损失函数会使( yi * yi^）>1 的样本损失皆为0，由此带来了稀疏解，使得 svm 仅通过少量的支持向量就能确定最终超平面。关于 SVM 支持向量机模型在之前有详细介绍，有兴趣的朋友可以打开链接。

2.9  squared_hinge 平方合页

1 def squared_hinge(y_true, y_pred):
2       y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred)
3       y_true = math_ops.cast(y_true, y_pred.dtype)
4       y_true = _maybe_convert_labels(y_true)
5       return backend.mean(
6           math_ops.square(math_ops.maximum(1. - y_true * y_pred, 0.)), axis=-1)

squared_hinge 平方合页损失函数与 hinge 类似，只有取最大值时加上平方值，与常规 hinge 合页损失函数相比，平方合页损失函数对离群值的惩罚更严厉，一般多于二分类计算。

2.10 categorical_hinge 多类合页

1 def categorical_hinge(y_true, y_pred):
2       y_pred = ops.convert_to_tensor(y_pred)
3       y_true = math_ops.cast(y_true, y_pred.dtype)
4       pos = math_ops.reduce_sum(y_true * y_pred, axis=-1)
5       neg = math_ops.reduce_max((1. - y_true) * y_pred, axis=-1)
6       return math_ops.maximum(0., neg - pos + 1.)

categorical_hinge 更多用于多分类形式

2.11 log_cosh

1 def log_cosh(y_true, y_pred):
2       y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred)
3       y_true = math_ops.cast(y_true, y_pred.dtype)
4 
5       def _logcosh(x):
6           return x + math_ops.softplus(-2. * x) - math_ops.cast(
7           math_ops.log(2.), x.dtype)
8 
9       return backend.mean(_logcosh(y_pred - y_true), axis=-1)

log_cosh 适用于回归，且比L2更平滑。它的计算方式是预测误差的双曲余弦的对数，对于较小的 x , log ( cosh(x))近似等于 x2 / 2 。对于大的 x，近似于  |x| - log2 。这表示 ‘logcosh’ 与均方误差算法大致相同，但是不会受到偶发性错误预测的强烈影响。

2.12 huber

 1 def huber(y_true, y_pred, delta=1.0):
 2       y_pred = math_ops.cast(y_pred, dtype=backend.floatx())
 3       y_true = math_ops.cast(y_true, dtype=backend.floatx())
 4       delta = math_ops.cast(delta, dtype=backend.floatx())
 5       error = math_ops.subtract(y_pred, y_true)
 6       abs_error = math_ops.abs(error)
 7       half = ops.convert_to_tensor_v2_with_dispatch(0.5, dtype=abs_error.dtype)
 8       return backend.mean( array_ops.where_v2(abs_error <= delta, 
 9              half * math_ops.square(error), 
10              delta * abs_error - half * math_ops.square(delta)),
11              axis=-1)

Huber 适用于回归, 它是平滑的平均绝对误差，优点是能增强平方误差损失函数对离群点的鲁棒性。当预测偏差小于 δ（delta）时，它采用平方误差,当预测偏差大于 δ 时，采用的绝对值误差，误差降到多小才变为平方误差由超参数δ。相比于均方误差，Huber 降低了对离群点的惩罚程度，所以 Huber  是一种常用的鲁棒的回归损失函数。也就是说当Huber 损失在 [0-δ，0+δ] 之间时，等价为MSE，而在 [-∞，δ] 和 [δ，+∞] 时相当于 MAE。这里超参数 δ（delta）的选择非常重要，因为这决定了对异常点的定义。当残差大于 δ（delta），应当采用 L1（对较大的异常值不那么敏感）来最小化，而残差小于超参数，则用 L2 来最小化。

2.13 poisson  泊松损失函数

1 def poisson(y_true, y_pred):
2       y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred)
3       y_true = math_ops.cast(y_true, y_pred.dtype)
4       return backend.mean(
5           y_pred - y_true * math_ops.log(y_pred + backend.epsilon()), axis=-1)

poisson 用于回归算法，一般用于计算事件发性的概率

2.14 cosine_similarity 余旋相似度

1 def cosine_similarity(y_true, y_pred, axis=-1):
2       y_true = nn.l2_normalize(y_true, axis=axis)
3       y_pred = nn.l2_normalize(y_pred, axis=axis)
4       return -math_ops.reduce_sum(y_true * y_pred, axis=axis)

预测值与真实标签的余弦距离平均值的相反数，它是一个介于-1和1之间的数字。当它是负数时在-1和0之间，0表示正交，越接近-1 表示相似性越大，值越接近1表示不同性越大，这使得它在设置中可用作损失函数。如果’ y_true ‘或’ y_pred '是一个零向量，余弦无论预测的接近程度如何，则相似度都为 0，而与预测值和目标值之间的接近程度无关。

2.15  kl_divergence 散度

1 def kl_divergence(y_true, y_pred):
2       y_pred = ops.convert_to_tensor_v2_with_dispatch(y_pred)
3       y_true = math_ops.cast(y_true, y_pred.dtype)
4       y_true = backend.clip(y_true, backend.epsilon(), 1)
5       y_pred = backend.clip(y_pred, backend.epsilon(), 1)
6       return math_ops.reduce_sum(y_true * math_ops.log(y_true / y_pred), axis=-1)

用于分类计算，通过衡量预测值概率分布到真值概率分布的相似度差异，在运动捕捉里面可以衡量未添加标签的运动与已添加标签的运动，进而进行运动的分类。

三、Optimizer 优化器

由于输入数据的特征很多，所以让计算损失函数变成很复杂，因此人们想出通过巧妙地利用梯度来计算损失函数最小值，而最常用的计算梯度方法就有梯度下降法和反向传播法。 
通过 model.compile (optimizer , loss , metrics) 中的 optimizer 优化器可绑定 SGD、AdaGrad、Adam、RMSProp 等多种算法。

1 @keras_export('keras.Model', 'keras.models.Model')
2 class Model(base_layer.Layer, version_utils.ModelVersionSelector):
3       def compile(self, optimizer='rmsprop', loss=None,
4               metrics=None,loss_weights=None,
5               weighted_metrics=None, run_eagerly=None,
6               steps_per_execution=None, **kwargs):

• optimizer：绑定优化器，用于绑定训练时所使用的优化器，一般有 SGD、AdaGrad、Adam、RMSProp 等。**
  **
• loss：绑定损失函数，有上述所介绍过的 15 种 损失函数可选择。**
  **
• metrics：绑定用于评估当前训练模型的性能参数，例如 [‘acc’ , ‘losses’] 正确率等，损失函数。评价函数和损失函数相似，只不过评价函数的结果只用于监测数据而不会用于训练过程中。
• loss_weights：参数类型 列表或字典，例如（0.7，0.3）。模型优化过程中，将损失函数最小化，是指对两个损失值求和之后最小化，那么这个loss_weights就是给这两个输出的损失值加权用的。

3.1 SGD 随机梯度下降法

1 class SGD(optimizer_v2.OptimizerV2):
2   def __init__(self,
3                learning_rate=0.01,
4                momentum=0.0,
5                nesterov=False,
6                name="SGD",
7                **kwargs):

参数说明

• learning_rate: float 类型，默认值为0.01，表示学习率
• momentum: float 类型，默认值为0，表示动量，大于等于0时可以抑制振荡
• nesterov: bool 类型，默认值为 False，是否启动 momentum 参数
• name: str类型，默认为 ‘SGD’，算法名称

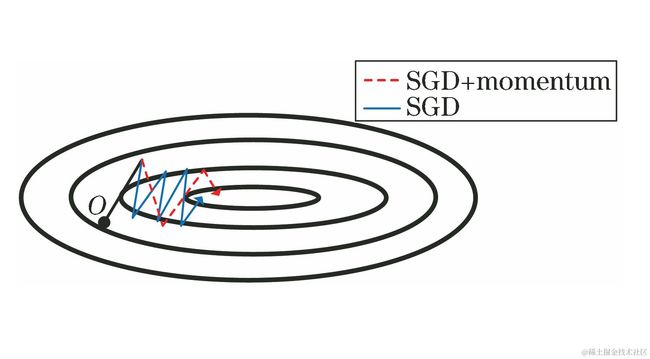
梯度下降法的实现原理已经详细介绍过，就是利用在微积分原理，对多元函数的输入参数求偏导数，把求得的各个参数的导数以向量的形式写出来就是梯度。梯度下降是迭代法的一种，通过不断小幅修改输入参数，求得切线斜率接近无限于0时的数据点（即鞍点）。通过多次递归方式，切线斜率就是无限接近于0，此就是数据点的最小值 。用此方法求得损失函数最小值，当损失函数到达最小值时，权重 w 和偏置量 h 则最符合数据集的特征。在无约束问题时，梯度下降是最常采用的方法之一。在使用 SGD 时，最重要的是选择合适的学习率 learning rate 比较困难 ，学习率太低会收敛缓慢，学习率过高会使收敛时的波动过大。

而梯度下降法也存在一定问题，因为所有参数都是用同样的 learning rate，在复杂的数据集情况下，损失函数就犹如一个小山丘，有多处小坑其梯度（偏导数）都为0，此时会有多个局部最小值（local  minimum）和一个是全局最小值（global minimum。到达局部最小值时梯度为0，如果 learning rate 太小，无论移向哪一方，其梯度都会增加，运算就会停止在坑中。因此，局部最小值就会被误认为全局最小值。
遇到此情况可尝试调节学习率 learning rate 或添加动量 momentum 加速收敛，但并不解决所有问题。

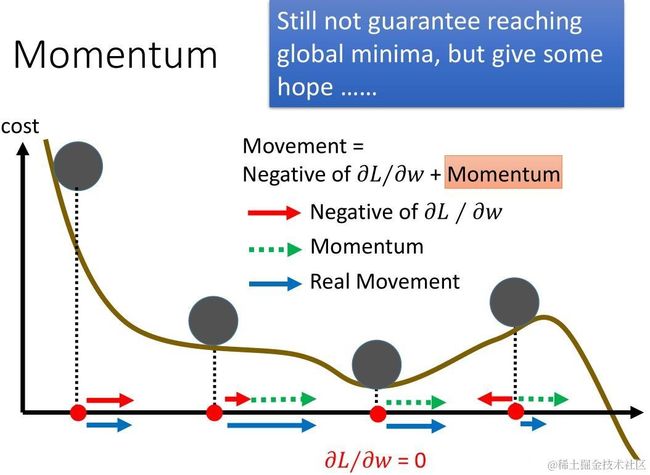
若想要加速收敛速度，可以尝试添加动量 momentum ，使用 momentum 的算法思想是：参数更新时在一定程度上保留之前更新的方向，同时又利用当前batch的梯度微调最终的更新方向，简言之就是通过积累之前的动量来加速当前的梯度。

在梯度方向改变时，momentum 能够降低参数更新速度，从而减少震荡；在梯度方向相同时，momentum可以加速参数更新， 从而增加冲过小坡的可能性。总而言之，momentum 能够加速SGD收敛，抑制震荡。

3.2  AdaGrad 算法

1 class Adagrad(optimizer_v2.OptimizerV2):
2   def __init__(self,
3                learning_rate=0.001,
4                initial_accumulator_value=0.1,
5                epsilon=1e-7,
6                name='Adagrad',
7                **kwargs):

参数说明

• learning_rate: float 类型，默认值为0.001，表示学习率
• initial_accumulator_value：float 类型，默认值为 0.1 ，累加器的初始值
• epsilon：float 类型，默认值为 1e-7，为的是避免计算时出现分母为 0 的特殊情况。
• name: str类型，默认为 ‘Adagrad’，算法名称

AdaGrad  也称自适应梯度法，它是 SGD 的一个优化算法，由 John Duchi 等人在 2011 年于 Adaptive Subgradient Methods for Online Learning and Stochastic Optimization 提出。相比起 SGD 它可以不断地自动调整学习率，当初期梯度矩阵平方的累积较小时，学习率相对比较快，到后期梯度矩阵平方的累积较大时，学习率会相对降低。

AdaGrad 的原理大概就是累计每一次梯度的矩阵平方，接着让学习率除以它的开方。这个的作用是为了不断地改变学习率。在前期，梯度累计平方和比较小，也就是 r 相对较小，这样就能够放大梯度对权重的影响力; 随着迭代次数增多，梯度累计矩阵平方和也越来越大，即 r 也相对较大，梯度对权重的影响力变得越来越小。

假设训练集中包含有 n 个样本 xi ，其对应的输出值为 yi，权重为 ωi ，学习率为 ϵ，则针对损失函数 L 的梯度 g 的计算公式如下：

r 为梯度矩阵平方的累积变量，初始值由 initial_accumulator_value 参数确定，默认为 0.1

计算权重的更新值 Δ ω，其中 δ 为小常数即参数 epsilon，默认值为 1e-7，为的是避免出现分母为 0 的特殊情况。而 ϵ 为学习率，默认值为0.001。由于分母越大值越小，这反映在图上就是在初始阶段，累积梯度矩阵平方值 r 较小，因此刚开发训练时变化会较快。但随着 r 值累计越来越大，变化会越来慢。但有个坏处就是有可能导致累计梯度矩阵平方 r 增速过大，权重的变化过早减小，学习率过早降低的情况。

最后更新权重值

3.3 RMSProp 算法

1 class RMSprop(optimizer_v2.OptimizerV2):
2       def __init__(self,
3                learning_rate=0.001,
4                rho=0.9,
5                momentum=0.0,
6                epsilon=1e-7,
7                centered=False,
8                name="RMSprop",
9                **kwargs):

• learning_rate: float 类型，默认值为0.001，表示学习率
• rho : float 类型 ，默认值0.9，衰减速率， 即是等式中的 ρ。
• epsilon : float 类型，默认值为 1e-7，为的是避免计算时出现分母为 0 的特殊情况。
• momentum ：float类型，默认值 0.0，即方程中的动量系数 α 。
• centered：bool类型，默认值为False。如果为True，则通过梯度的估计方差,对梯度进行归一化；如果False，则由未centered的第二个moment归一化。将此设置为True有助于模型训练，但会消耗额外计算和内存资源。默认为False。
• name：str类型，默认为 ‘RMSprop’，算法名称

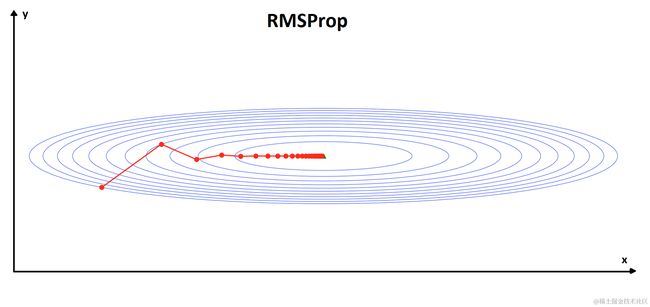
RMSProp 算法是 AdaGrad 算法的改量版，上面说过AdaGrad最大的问题在于当累计梯度矩阵平方 r 早期增速过大时，会导致权重的变化过早减小，学习率过早降低的情况。为解决这个问题，RMSProp 加入了衰减速率参数 rho ，使梯度矩阵平方的累积变量 r 值增加的速度更加平稳，从而避免权重的变化过早减小，学习率过早降低的情况。

假设训练集中包含有 n 个样本 xi ，其对应的输出值为 yi，权重为 ωi ，学习率为 ϵ，则针对损失函数 L 的梯度 g 的计算公式如下：

r 为梯度矩阵平方的累积变量，它的计算方式与AdaGrad 略有不同，在原有基础上加入衰减速率 ρ，默认值为 0.9，r 的变化率会受到衰减率 ρ 设置的影响。

计算权重的更新值 Δ ω，其中 δ 为小常数即参数 epsilon，默认值为 1e-7，为的是避免出现分母为 0 的特殊情况。而 ϵ 为学习率，默认值为0.001。与 AdaGrad相似，在累积梯度矩阵平方值 r 较小，因此刚开发训练时变化会较快。但随着 r 值累计越来越大，变化会越来慢。然而不同在于，由于 r 的取值加入了衰减速率 ρ 的控制，所以其减速现象明显得以抑制，避免了权重的变化过早减小，学习率过早降低的情况。若要调整权重更新值 Δ ω 的占比，也可设置动量系数 α。

由于动量系数 α （即参数 momentum ）默认值为 0，所以默认情况下权重更新值 Δ ω 与 AdaGrad 类似。

最后更新权重值

3.4 Adam  算法

1 class Adam(optimizer_v2.OptimizerV2):
2       def __init__(self,
3                learning_rate=0.001,
4                beta_1=0.9,
5                beta_2=0.999,
6                epsilon=1e-7,
7                amsgrad=False,
8                name='Adam',
9                **kwargs):

• learning_rate: float 类型，默认值为0.001，表示学习率
• beta_1：float 类型，默认值为 0.9 ，指定一阶矩估计的指数衰减率 ρ1
• beta_2：float 类型，默认值为 0.999 , 指定二阶矩估计的指数衰减率 ρ2
• epsilon：float 类型，默认值为 1e-7，为的是避免计算时出现分母为 0 的特殊情况。
• amsgrad: bool 类型，默认值为 False，是否应用该算法的 AMSGrad 变体
• name: str类型，默认为 ‘Adam’，算法名称

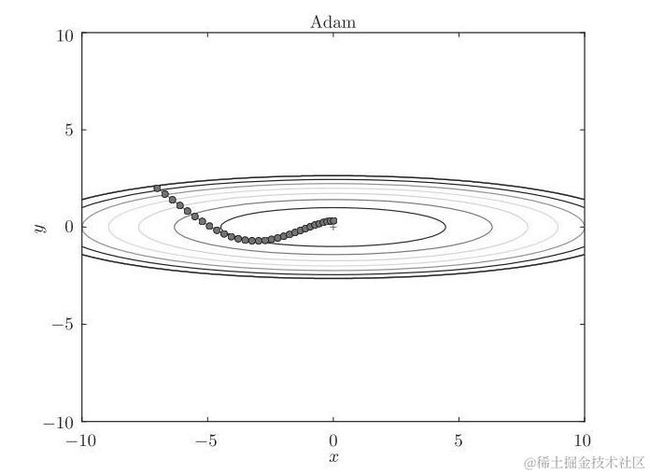
Adam 相当于把 AdaGrad 算法融合了动量 momentum 的概念，整合出来的新算法，由 Diederik Kingma 等人 2014 年在 A Method for Stochastic Optimization .arXiv:1412.6980 提出。实现偏置校正是 Adam 的特征，这使 Adam 算法的运算效率更高。它分别指定了一阶矩估计的指数衰减率 ρ1 和二阶矩估计的指数衰减率 ρ2，随着训练集的循环会不断更新一阶矩偏差 s^ 和 二阶矩偏差 r^，从而计算出计算权重的更新值 Δ ω 。

假设训练集中包含有 n 个样本 xi ，其对应的输出值为 yi，权重为 ωi ，学习率为 ϵ，则针对损失函数 L 的梯度 g 的计算公式如下：

Adam 把 RMSProp 中的梯度矩阵平方的累积变量的算法转换成计算一阶矩偏差 s^  和 二阶矩偏差 r^，最后用它们的比值 s ^ / sqrt( r ^ ) 得出结果 。这样做梯度经过偏置校正，每一次迭代学习率都有一个固定范围，因此学习流程更加平稳。s 与 r 的初始值均为 0 ，指数衰减率 ρ1、ρ2 的初始值默认为 0.9 和 0.999 。每次循环，系统都会根据累积变量 s、r 修正偏差值 s^、 r^。

更新一阶矩累积变量

更新二阶矩估计累积变量

跟随训练，循环修正一阶矩的偏差值 s^

跟随训练，循环修正二阶矩的偏差值 r^

计算权重的更新值 Δ ω，其中 δ 为小常数即参数 epsilon，默认值为 1e-7，为的是避免出现分母为 0 的特殊情况。而 ϵ 为学习率，默认值为0.001。

最后更新权重值

四、激活函数

在第一节曾经介绍到，每个神经元要传播到下一层时，都需要通过激活函数，我们可以把这看成是输入信号的加权和转化为输出信号的的一个过程，它为神经元提供了模拟非线性数据集所必需的非线性特征。正因为大部分神经元之间的数据都存在非线性关系，所以激活函数都非线性的，要不然隐藏层就会失去其意义。最常见的激活函数有阶跃激活函数、Sigmoid 激活函数、ReLU激活函数、Tanh 激活函数、Softmax激活函数等，下面将一一介绍。

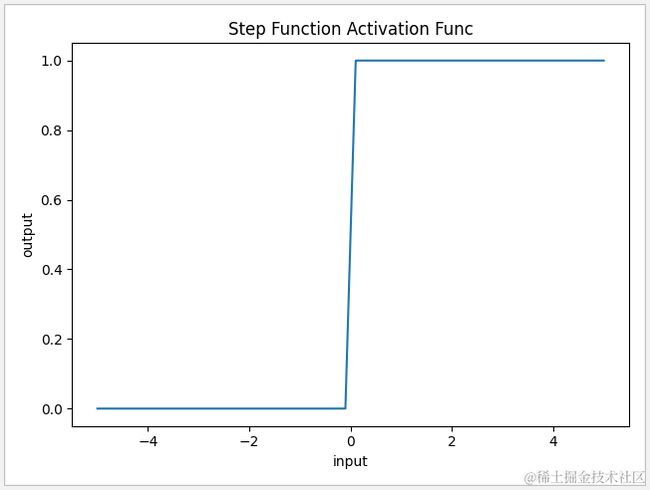
4.1 阶跃激活函数

这是最简单的一种激活方式，它以0为临界时，当输入值 input 小于0 时返回 0，大于 0 时返回 1。由于它的值呈阶梯式变化，因为被称为阶跃激活函数（也称阈值激活函数）。但是这简单方法的缺点也是非常明显的。 首先它是不连续且不光滑的，这就导致在反向传播时这一层很难学习。 其次阶跃函数有着 “非黑即白” 的特性，所以一般只适用于简单的二分类非线性激活。由于它在 x=0 时不具有连贯性，因此不适合用于梯度下降的数据训练中。

 1 def func(x):
 2     return np.array(x>0)
 3 
 4 x=np.linspace(-5,5,50)
 5 y=func(x)
 6 plt.xlabel('input')
 7 plt.ylabel('output')
 8 plt.title('Step Function Activation Func')
 9 plt.plot(x,y)
10 plt.show()

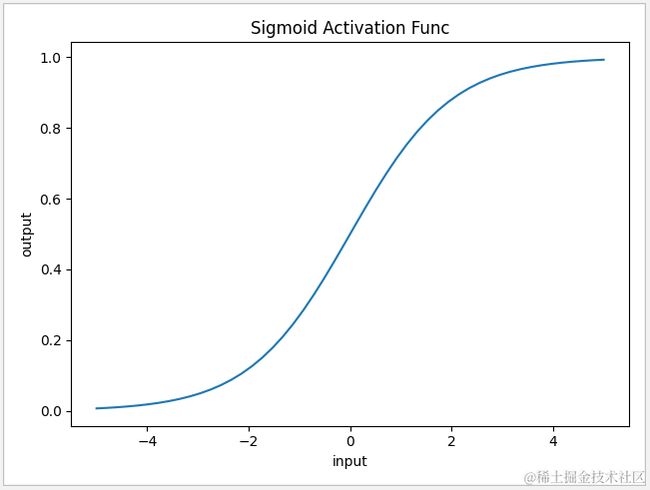
4.2 Sigmoid 激活函数

sigmoid 的输出函数由 f(x)=1/(1+exp(-x)) 确定，在tensorflow 中可以通过 tf.sigmoid 调用，由于形状很像 S，因此命名为 sigmoid 。相比起阶跃激活函数，sigmoid 在0~1之间值过渡显得更平滑，但在两个边缘值梯度都无穷接近于 0，这非常容易造成 “梯度消失”，因此为优化训练增加了难度。此外 sigmoid 函数输出值在 0 到 1 之间，其均值为0.5，不符合神经网络内数值期望为 0 的设想。一般情况 sigmoid 用于隐藏层的激活或输出层的回归。

 1 def func(x):
 2     return 1/(1+np.exp(-x))
 3 
 4 x=np.linspace(-5,5,50)
 5 y=func(x)
 6 plt.xlabel('input')
 7 plt.ylabel('output')
 8 plt.title('Sigmoid Activation Func')
 9 plt.plot(x,y)
10 plt.show()

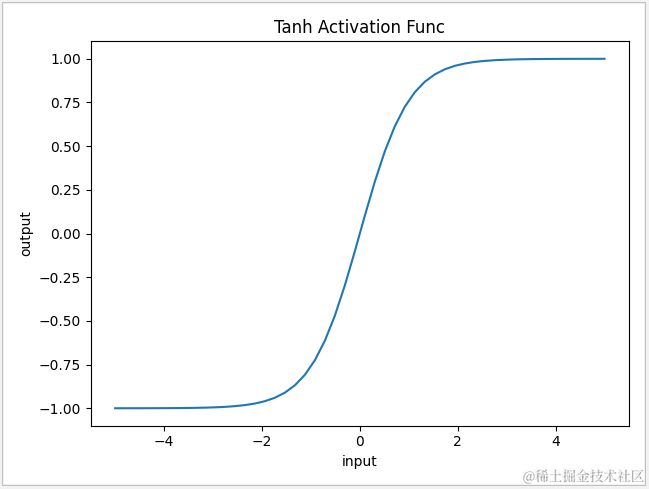
4.3 Tanh 激活函数

tanh 双曲正切激活函数公式由 f(x)=(1-exp(-2x)) / (1+exp(-2x)) 确定，在tensorflow 中可以通过 tf.tanh 调用。它相当于 sigmoid 的改良版，其输入值从 -1 到 1 之间均值为0，这正解决了 sigmoid 均值为0.5 的缺陷，并且它的切线比 sigmoid 更陡峭。然而 tanh 的两个边缘值梯度也是无穷接近于 0， 并不能解决 sigmoid “梯度消失” 的问题。一般情况 tanh 会用于隐藏层的激活或输出层的回归。

 1 def func(x):
 2     return (1-np.exp(-2*x))/(1+np.exp(-2*x))
 3 
 4 x=np.linspace(-5,5,50)
 5 y=func(x)
 6 plt.xlabel('input')
 7 plt.ylabel('output')
 8 plt.title('Tanh Activation Func')
 9 plt.plot(x,y)
10 plt.show()

4.4 ReLU激活函数

ReLU 激活函数是分段线性函数，它能在多层激活时捕获非线性特征，在tensorflow 中可以通过 tf.nn.relu 调用。在输入为正数的时候，其输出值为无穷大，弥补了sigmoid函数以及tanh函数的梯度消失问题。而且 ReLU 函数只有线性关系，因此不管是前向传播还是反向传播，计算速度都比 sigmod 和 tanh 要快。ReLU 最大的问题在于当输入值小于0 时，梯度一直为0，因此产生梯度消失问题。尽管如此，ReLU 也是最常用的激活函数之一，常用于隐藏层的激活和输出层的回归。

 1 def func(x):
 2     return np.maximum(0,x)
 3 
 4 x=np.linspace(-5,5,50)
 5 y=func(x)
 6 plt.xlabel('input')
 7 plt.ylabel('output')
 8 plt.title('ReLU Activation Func')
 9 plt.plot(x,y)
10 plt.show()

4.5 Leaky ReLU 激活函数

Leaky ReLU 激活函数是 ReLU 的改良版，在 tensorflow 中可以通过 tf.nn.leaky_relu 调用。它是为了改善 ReLU 输入值小于0 时，梯度一直为 0 的问题而设计的。在 Leaky ReLU 中当输入值小于0时，输出值将为 ax，因此不会造成神经元失效。当神经元输出值有可能出现小于0的情况，就会使用 Leaky ReLU 输出，常用于隐藏层的激活和输出层的回归。

 1 def func(x,a=0.01):
 2     return np.maximum(a*x,x)
 3 
 4 x=np.linspace(-5,5,50)
 5 y=func(x)
 6 plt.xlabel('input')
 7 plt.ylabel('output')
 8 plt.title('Leaky ReLU Activation Func')
 9 plt.plot(x,y)
10 plt.show()

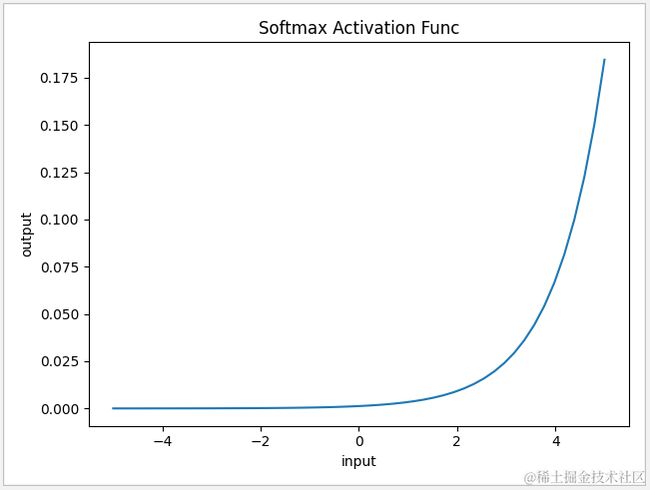
4.6 Softmax 函数

Softmax 的计算公式如下，在tensorflow中可直接通过 tf.nn.softmax 调用，一般用作输出层的分类激活函数，它表示每个分类的输出概率，所有输出概率合共为 1。

 1 def func(x):
 2     return np.exp(x)/np.sum(np.exp(x))
 3 
 4 x=np.linspace(-5,5,50)
 5 y=func(x)
 6 plt.xlabel('input')
 7 plt.ylabel('output')
 8 plt.title('Softmax Activation Func')
 9 plt.plot(x,y)
10 plt.show()

到此归纳总结一下阶跃激活函数、Sigmoid 激活函数、Tanh 激活函数、ReLU激活函数、Leaky ReLU 激活函数、Softmax 函数和恒等输出的应用场景。一般阶跃激活函数只用于简单的二分类输出，Sigmoid 和 Tanh 激活函数用于隐藏层的输出或输出层的回归，但两者皆会存在输出梯度消失的风险。ReLU 和 Leaky ReLU 激活函数可用于隐藏层的输出或输出层的回归，它能消除梯度消失的风险，而且性能高。当输出值为正值时可使用 ReLU，当输出值存在负值的可能时使用 Leaky ReLU 。而在输出层的分类计算可使用 Softmax 函数，简单分类也可用 Sigmoid 逻辑回归，在输出层的回归计算可使用恒等函数，即对输入信息不作任何修改直接输出。

五、多层感知机 MLP

多层感知机 MLP，它以层为组织搭建：至少包含一个一个输入层，一个或多个隐藏层，一个输出层。数据通过输入层输入，通过多个隐藏层传递，通过输出层输出，过程中层与层之间没有信息反馈，因此被称为前馈神经网络 FNN。当数据传到输出层时，系统会把输出数据与正确数据进行对比，把梯度反馈同时更新权重，如此反复循环，最后把误差减到最小。

5.1 三层分类感知机

下面从最简单的分类感知机开始介绍，用 mnist 数据进行测试，当中只包含一个输入层，一个隐藏层，一个输出层 。为了方便讲解，第一个例子先用 tensorflow 1.x 版本进行讲解，先用占位符设定输入数据X，y。由于 mnist 的图像是2828 像素，0~9 的数字，这个感知机的目的就是把 784 特征的数据分成 0~9 的10类，所以隐藏层参数形状应为 [784,10]，h 为 [10] 。通过公式 y=wx+h 进行计算，最后 softmax 分类函数输出。由于是分类计算，所以损失函数选用了常用的交叉熵损失函数，算法使用 Adam 算法，把学习率设置为 0.3 。输入测试数据，分多批每批 500 个进行训练，每隔200个输出一次正确率，如此循环训练10次。可见10次后，测试数据的准确率已经达到 91%，最后查看测试数据的准确率，也将近有 90%。
这就是最简单的三层感知机 ，可见其结构原理比较简单，然后使用 tensorflow 1.x 的方法略显繁琐。下面介绍一下多层感知机，使用 tensorflow 2.x 进行编写，可读性会更高。

def test():
    tf.disable_eager_execution()
    X=tf.placeholder(tf.float32,[None,784])
    y=tf.placeholder(tf.float32,[None,10])
    # 隐藏层参数w0,h0
    w0=tf.Variable(tf.random_normal([784,10],stddev=0.1))
    h0=tf.Variable(tf.random_normal([10],stddev=0.1))
    # 计算 logits
    logits=tf.matmul(X,w0)+h0
    # 计算输出值 y_
    y_=tf.nn.softmax(logits)
    # 交叉熵损失函数
    cross_entropy=tf.nn.softmax_cross_entropy_with_logits(logits=logits,labels=y)
    cross_entropy=tf.reduce_mean(cross_entropy)
    # Adam 算法,学习率为 0.3
    train_step=tf.train.AdamOptimizer(0.3).minimize(cross_entropy)
    # 计算准确率
    correct=tf.equal(tf.argmax(y_,1),tf.argmax(y,1))
    accuray=tf.reduce_mean(tf.cast(correct,tf.float32))
     # 计入测试数据
    (X_train,y_train),(X_test,y_test)=datasets.mnist.load_data()
    with tf.Session() as session:
        session.run(tf.global_variables_initializer())
        #训练10次
        for epoch in range(10):
            #分批处理训练数据，每批500个数据
            start=0
            n=int(len(X_train)/500)
            print('---------------epoch'+str(epoch)+'---------------')
            for index in range(n):
                end = start + 500
                batch_X,batch_y=X_train[start:end],y_train[start:end]
                batch_X=batch_X.reshape(500,784)
                batch_y=keras.utils.to_categorical(batch_y)
                #分批训练
                train_,cross,acc=session.run([train_step,cross_entropy,accuray]
                       ,feed_dict={X:batch_X,y:batch_y})
                if index%200==0:
                    # 每隔200个输出准确率
                    print('  accuray:'+str(acc*100))
                start+=500
        #处理测试数据输出准确率
        X_test=X_test.reshape(-1,784)
        y_test=keras.utils.to_categorical(y_test)
        accuray=session.run(accuray,feed_dict={X:X_test,y:y_test})
        print('--------------test data-------------\n  accuray:'+str(accuray*100))            

运行结果

5.2 多层感知机

前面介绍过 tensorflow 2.0 已经融入 keras 库，因此可以直接使用层 layer 的概念，先建立一个 model，然后通过 model.add(layer) 方法，加入每层的配置。完成层设置后，调用 model.compile(optimizer, loss, metrics) 可绑定损失函数和计算方法。最后用 model.fit() 进行训练，分批的数据量和重复训练次数都可以直接通过参数设置。

1 @keras_export('keras.Model', 'keras.models.Model')
2 class Model(base_layer.Layer, version_utils.ModelVersionSelector):
3   　　def fit(self, x=None,y=None,batch_size=None, epochs=1,
4           verbose='auto',callbacks=None, validation_split=0.,
5           validation_data=None, shuffle=True, class_weight=None,
6           sample_weight=None,initial_epoch=0, steps_per_epoch=None,
7           validation_steps=None,validation_batch_size=None,
8           validation_freq=1,max_queue_size=10,
9           workers=1, use_multiprocessing=False):

参数说明

• x：输入数据。如果模型只有一个输入，那么x的类型是 array，如果模型有多个输入，那么x的类型应当为list，list的元素是对应于各个输入的 array
• y：输入数据的验证标签，array
• batch_size：整数，指定进行梯度下降时每个batch包含的样本数。训练时一个batch的样本会被计算一次梯度下降，使目标函数优化一步。
• epochs：整数，训练终止时的epoch值，训练将在达到该epoch值时停止，当没有设置initial_epoch时，它就是训练的总轮数，否则训练的总轮数为epochs - inital_epoch
• verbose：日志显示，0为不在标准输出流输出日志信息，1为输出进度条记录，2为每个epoch输出一行记录
• callbacks：list，其中的元素是keras.callbacks.Callback的对象。这个list中的回调函数将会在训练过程中的适当时机被调用，参考回调函数
• validation_split：0~1之间的浮点数，用来指定训练集的一定比例数据作为验证集。验证集将不参与训练，并在每个epoch结束后测试的模型的指标，如损失函数、精确度等。注意，validation_split的划分在shuffle之前，因此如果你的数据本身是有序的，需要先手工打乱再指定validation_split，否则可能会出现验证集样本不均匀。
• validation_data：形式为（X，y）的 tuple，是指定的验证数量集。设定此参数后将覆盖 validation_spilt。
• shuffle：布尔值或字符串，一般为布尔值，表示是否在训练过程中随机打乱输入样本的顺序。若为字符串“batch”，则是用来处理HDF5数据的特殊情况，它将在batch内部将数据打乱。
• class_weight：字典，将不同的类别映射为不同的权值，该参数用来在训练过程中调整损失函数（只能用于训练）
• sample_weight：权值的numpy array，用于在训练时调整损失函数（仅用于训练）。可以传递一个1D的与样本等长的向量用于对样本进行1对1的加权，或者在面对时序数据时，传递一个的形式为（samples，sequence_length）的矩阵来为每个时间步上的样本赋不同的权。这种情况下请确定在编译模型时添加了sample_weight_mode=’temporal’。
• initial_epoch: 从该参数指定的epoch开始训练，在继续之前的训练时有用。
• validation_steps：验证数据的批次数
• validation_batch_size：每批次验证数据的数量

相比起 tensorflow 1.x 可读性更强，而且能支持多平台运行，它去除了占位符的概念，开发时无受到 session 的约束，而是直接通过函数来调用。
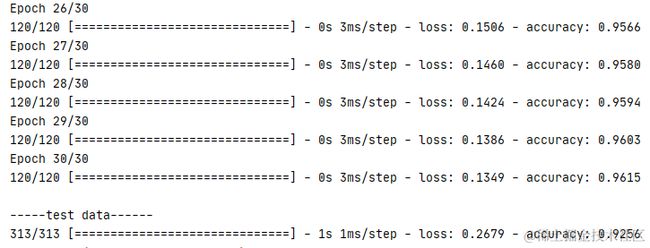
还是以 mnist 为例子，通过 5 层的训练，神经元数目从 784 逐层下降 200、100、60、30、10，最后通过 softmax 函数输出。通过 5 层的神经元，正确率可提升到将近 93%。

 1 def getModel():
 2     # 神经元数目从 784 逐层下降 200、100、60、30、10，最后通过 softmax 函数输出
 3     model=keras.models.Sequential()
 4     model.add(layers.Flatten(input_shape=(28,28)))
 5     model.add(layers.Dense(units=200,activation='relu'))
 6     model.add(layers.Dense(units=100,activation='relu'))
 7     model.add(layers.Dense(units=60,activation='relu'))
 8     model.add(layers.Dense(units=30,activation='relu'))
 9     model.add(layers.Dense(10,activation='softmax'))
10     return model
11 
12 def test():
13     # 获取数据集
14     (X_train,y_train),(X_test,y_test)=keras.datasets.mnist.load_data()
15     X_train,y_train=tf.convert_to_tensor(X_train,tf.float32) , tf.convert_to_tensor(y_train,tf.float32)
16     # 建立 model
17     model=getModel()
18     # 使用 SGD 梯度下降法，学习率为 0.003
19     # 使用交叉熵算法
20     model.compile(optimizer=optimizers.SGD(0.003),
21                   loss=losses.sparse_categorical_crossentropy,
22                   metrics=['accuracy'])
23     # 绑定 tensorboard 对日志数据进行监测
24     callback=keras.callbacks.TensorBoard(log_dir='logs', histogram_freq=1, embeddings_freq=1)
25     # 重复训练30次，每 500 个作为一批
26     model.fit(X_train,y_train,epochs=30,batch_size=500，callbacks=callback)
27     # 输出测试数据准确率
28     X_test, y_test = tf.convert_to_tensor(X_test, tf.float32), tf.convert_to_tensor(y_test, tf.float32)
29     print('\n-----test data------')
30     model.fit(X_test,y_test)

运行结果

通过 keras.callbacks.TensorBoard(log_dir=‘日志路径’）直接绑定日志目录，训练时绑定回调函数即可将检测数据写入日志 model.fit (x=测试数据, y=正确输出结果,batch_size=分批运行时每批数量, epochs=训练重复次数, callbacks=绑定回调），最后通过命令 “ tensorboard --logdir=日志路径 “ 即可在浏览器 http://localhost:6006/ 上查看日志。

5.3 多层感知机回归测试

以波士顿房价作为测试数据集，尝试使用多层感知机对未来房价进行预测，看一下测试结果如何。首先建好 Model，测试数据集有13个特征，把神经元扩展到 20、50 个。由于是回归计算，所以输出层使用 sigmoid 所以输出值只需要一列。由于 boston 数据集中有多列数据，大小不一，所以在输入可以前先利用 MinMaxScaler 进行归一化处理。注意测试数据集中 y_train 和 y_test只有一列，所以在归一化处理前先要先利用 y_train[:,np.newaxis] 或其他方式进行行列调换，不然系统将报错。然后使用 Adam 算法，huber 损失函数进行10次训练。
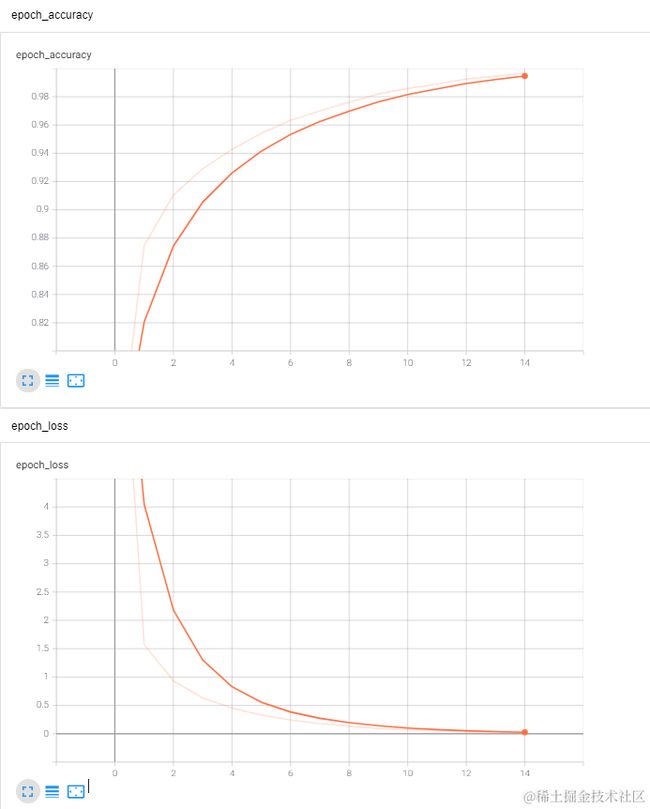
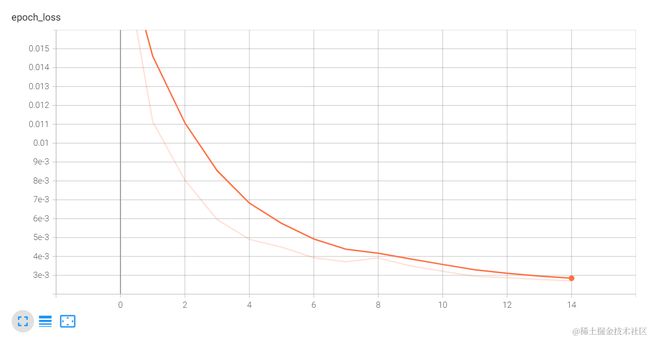
完成训练后，对比测试数据与原数据的值。可见经过15次训练后，损失率已到达0.003 以下，测试值与真实值已经相当接近。

 1 def getModel():
 2     # 神经元从13到20、50，输出层使用sigmoid激活函数
 3     model=keras.models.Sequential()
 4     model.add(layers.Flatten())
 5     model.add(layers.Dense(units=20,activation='relu'))
 6     model.add(layers.Dense(units=50,activation='relu'))
 7     model.add(layers.Dense(units=1,activation='sigmoid'))
 8     return model
 9 
10 def test():
11     # Boston房价测试数据集
12     (X_train,y_train),(X_test,y_test)=keras.datasets\
13         .boston_housing.load_data()
14     # 数据多列大于1，所以先把数据进行归一化处理
15     scale = MinMaxScaler()
16     X_train = scale.fit_transform(X_train)
17     X_test = scale.fit_transform(X_test)
18     y_train=y_train[:,np.newaxis]
19     y_train=scale.fit_transform(y_train)
20     y_test=y_test[:,np.newaxis]
21     y_test=scale.fit_transform(y_test)
22     # 生成 Model
23     model=getModel()
24     # 使用Adam算法，学习率为0.003，huber损失函数
25     model.compile(optimizer=optimizers.Adam(0.003)
26                   ,loss=losses.huber)
27     # 回调生成日志记录
28     callback=keras.callbacks.TensorBoard(log_dir='logs'
29                   , histogram_freq=1, embeddings_freq=1)
30     # 训练数据训练
31     model.fit(X_train,y_train,10,epochs=15,callbacks=callback)
32     # 计算测试输出数据
33     y_hat=model.predict(X_test)
34     # 画图对象测试输出数据与真实输出数据差别
35     x=np.linspace(0,1,len(y_hat))
36     # 把单列数据变形返回单行数据
37     y1=y_hat.flatten()
38     y2=y_test.flatten()
39     # 画出对比图
40     plt.scatter(x,y1,marker='^',s=60)
41     plt.scatter(x,y2,marker='*',s=60)
42     plt.title('Boston_Housing Test vs Actual')
43     plt.legend(['test data','actual data'])
44     plt.show()

运行结果

对比图

损失函数图

六、利用 Dropout 进行正则化

6.1 回顾 L1/L2 正则化处理

过拟合就是说模型在训练数据上的效果远远好于在测试集上的性能，参数越多，模型越复杂，而越复杂的模型越容易过拟合。记得曾经介绍过通过正则化处理过拟合问题，常用的处理方式方式 L1/ L2 两种：

• L1 正则化则是以累加绝对值来计算惩罚项，因此使用 L1 会让 W(i) 元素产生不同量的偏移，使某些元素为0，从而产生稀疏性，提取最有效的特征进行计算。
• L2 正则化则是使用累加 W 平方值计算惩罚项，使用 L2 时 W(i) 的权重都不会为0，而是对每个元素进行不同比例的放缩。 此时可以考虑正则化，通过设置正则项前面的 hyper parameter，来权衡损失函数和正则项，减小参数规模，达到模型简化的目的，从而使模型具有更好的泛化能力。

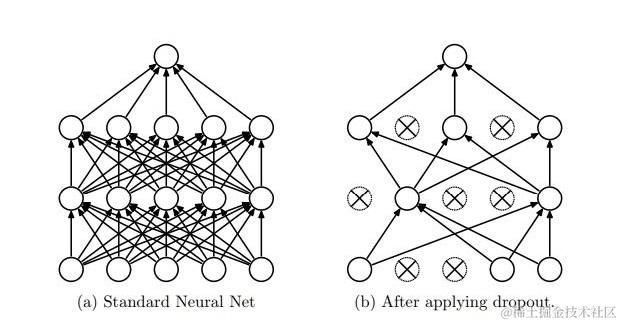
6.2 Dropout 优化处理

而在 MLP 中也提供了 dropout 对过拟合的数据进行正则化处理，它的处理方式是在学习阶段，设置丢失神经元的概率，当一个神经元被丢弃时，它的输出值被设为0。由于神经元在每次新的训练中被随机丢弃，所以每个训练阶段其丢失的神经元都不相同。在面对复杂的数据集时，很多时候 dropout 会跟 L2 正则化同时使用以降低过拟合情况。

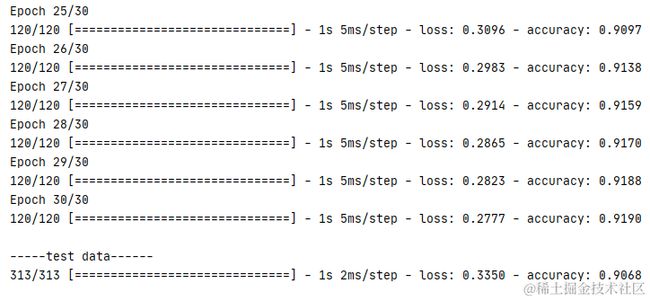
下面的例子以 mnist 数据集为例子，经过五层的训练，每层训练都加入 5% 的丢失率进行正则化处理。反复训练 30 次后，测试数据的准确率依然达到 90%，可见 dropout 对避免过拟合是有一定的效果。

 1 def getModel():
 2     # 神经元数目从 784 逐层下降 200、100、60、30、10，最后通过 softmax 函数输出
 3     model=keras.models.Sequential()
 4     model.add(layers.Flatten(input_shape=(28,28)))
 5     model.add(layers.Dense(units=200,activation='relu'))
 6     model.add(layers.Dropout(rate=0.05))
 7     model.add(layers.Dense(units=100,activation='relu'))
 8     model.add(layers.Dropout(rate=0.05))
 9     model.add(layers.Dense(units=60,activation='relu'))
10     model.add(layers.Dropout(rate=0.05))
11     model.add(layers.Dense(units=30,activation='relu'))
12     model.add(layers.Dropout(rate=0.05))
13     model.add(layers.Dense(units=10,activation='softmax'))
14     return model
15 
16 def test():
17     # 获取数据集
18     (X_train,y_train),(X_test,y_test)=keras.datasets.mnist.load_data()
19     X_train,y_train=tf.convert_to_tensor(X_train,tf.float32) , tf.convert_to_tensor(y_train,tf.float32)
20     # 建立 model
21     model=getModel()
22     # 使用 SGD 梯度下降法，学习率为 0.003
23     # 使用交叉熵算法
24     model.compile(optimizer=optimizers.SGD(0.003),
25                   loss=losses.sparse_categorical_crossentropy,
26                   metrics=['accuracy'])
27     # 绑定 tensorboard 对日志数据进行监测
28     callback=keras.callbacks.TensorBoard(log_dir='logs', histogram_freq=1, embeddings_freq=1)
29     # 重复训练50次，每 500 个作为一批
30     model.fit(X_train,y_train,epochs=30,batch_size=500,callbacks=callback)
31     # 输出测试数据准确率
32     X_test, y_test = tf.convert_to_tensor(X_test, tf.float32), tf.convert_to_tensor(y_test, tf.float32)
33     print('\n-----test data------')
34     model.fit(X_test,y_test)

运行结果

本篇总结

本文主要介绍了MSE、MAE、CEE 、Hinge、Huber 等 15 个常用损失函数的计算方式和使用场景，分析 SGD、AdaGrad、Adam、RMSProp 4类优化器的公式原理，对阶跃激活函数、Sigmoid 激活函数、ReLU激活函数、Leaky ReLU 激活函数、Tanh 激活函数、Softmax激活函数等进行讲解。
多层感知器 MLP 是深度学习的基础，本文通过分类、回归的使用例子对 MLP 的使用进行介绍。最后，讲解了如何使用 dropout 正则化对复杂类型的数据集进行优化处理。
希望本篇文章对相关的开发人员有所帮助，由于时间仓促，错漏之处敬请点评。