数据结构之链表

引言

链表，是实现顺序表的一种常用方式。通过链接关系来显式表示元素之间的顺序关系。
常见的链表结构共分为五种：

1. 单向简单链表结构：只有一个属性域self._head。在进行表内元素操作时，只支持从前到后遍历，时间复杂度较高
2. 单向改进链表结构：增加了一个属性域self._rear，能够在O(1)的复杂度对表尾元素进行增加操作。
3. 单向循环链表结构：链表是一个环状结构。与普通链表的差异在于扫描循环的结束控制
4. 双向简单链表结构：链表中每个元素都有三个属性，既能记录前继结点又能记录后驱结点。
5. 双向循环链表结构：顾名思义

结点类

在定义链表结构类之前，我们需要首先了解链表内的每个元素的结构和属性。根据前面介绍可知，对于普通的单向链表结构，其元素有两个属性：该节点代表的值以及其后驱结点的位置；

而对于双向链表结构，其元素要有三个属性，该节点代表的值、其后驱结点的位置以及前继结点的位置。

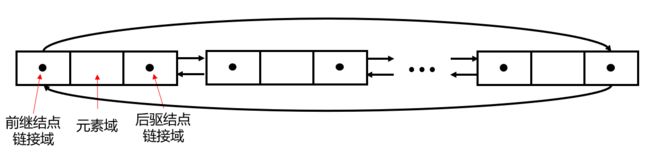
废话不多说直接上代码

# 单向链表结点类
class LNode():
    def __init__(self, elem, next_=None):
        self.elem = elem
        self.next = next_

在LNode类中，对于属性名next_，需要加上下划线_，将其与Python中标准函数next()区分开来。

# 双向链表结点类
class DLNode(LNode):
    def __init__(self, elem, prev = None, next_=None):
        LNode.__init__(self, elem, next_)
        self.prev = prev

在定义双向结点类DLNode时，选择继承父类LNode的相关属性（DLNode表示 DoubleLinkNode）

单向简单链表结构

实现单链表的基本需求是：

• 能够找到链表中的第一个元素
• 根据链表中的任一元素，可以找到其对应的下一个元素

像列表、元组这样的顺序结构固然可以简单地通过将元素保存在连续的存储区进行实现，但其需要消耗大量的存储空间，且在进行查找、变更等操作时十分复杂。

接下来本博客会重点介绍一下单向简单链表的构建和功能实现。

# 单链表类
class LList():
    # 初始化
    def __init__(self):
        # 由_开头的属性名或者函数名不宜在类外进行调用
        # 由__开头（但不以__结尾的）不能在类外用该名字进行访问
        # 如果访问 则会报错： object has no attribute
        self._head = None

首先，定义一个__init__函数来进行类的初始化，设置_head域来充当C++等语言中的指针。将属性名定义为_head是为了保护该属性不在类外被调用。

下面，将着重介绍链表类的各个功能函数的实现

is_empty函数

对于一个链表，首先需要判断其是否非空，非空链表和空链表在增加删除元素等方面均有较大不同。

# 判断链表是否非空
def is_empty(self):
    return (self._head is None)

__len__函数

对于一个链表，通过函数来计算该链表的长度。Python的内置函数len可以自动调用用户定义类里的相关函数__len__.

# 计算链表的长度
def __len__(self):
    p = self._head

    sum = 0
    while p is not None:    # 表尾结点会进入while循环
        sum += 1
        p = p.next
        
    return sum

prepend函数

在链表的前端添加新元素，需要注意要将原首元素链接到新元素（结点）后面，即应满足：new_element.next = self._head

# 在表头添加元素
def prepend(self, elem):
    self._head = LNode(elem, self._head)

append函数

由于链表的结构性质，当需要在链表的末端添加新元素时，必须将整个链表从前向后遍历一遍，找到尾结点，将新结点链接到尾结点之后。

# 在表尾添加元素
def append(self, elem):
    p = self._head
    while p.next is not None:
        p = p.next
    p.next = LNode(elem)

insert函数

倘若需要在链表之中插入新元素（按位置进行索引），则需要首先从前向后定位到插入新元素的位置，将新元素与定位的结点及其之后的结点建立链接关系。

# 指定位置添加元素
def insert(self, position, elem):
    if position < 0 or position > self.__len__():
        raise LinkedListUnderflow('in insert')
    
    if position == 0:
    	self.prepend(LNode(elem))
    pos = 1    # 方便理解
    # 当position = self.__len__时，即是append操作
    p = self._head
    while pos != position:
        p = p.next
        pos += 1
        
    node = LNode(elem)
    node.next = p.next
    p.next = node

这个insert函数时prepend函数和append函数更加一般化的函数表达，其涵盖了这两个函数的功能，并能根据任意指定位置来进行结点增加的操作。

pop函数

当需要将表头元素删除时，需要注意删除后_head域的指向问题，并且需要考虑链表为空的情况，此时我们需要定义一个异常类来帮助我们处理异常。

# 定义异常类
class LinkedListUnderflow(ValueError):
    pass

由于在链表类里会出现的异常情况基本只有对空链表进行删除操作，故我们定义的类是继承ValueError类的

# 删除表头元素，并返回其值
def pop(self):
    if self._head is None:
        raise LinkedListUnderflow('in pop')
        
    e = self._head.elem
    self._head = self._head.next
    return e

pop_last函数

当需要删除表尾元素时，需要从前向后遍历到尾结点，对其进行删除。在进行该操作时，必须考虑到链表有一个元素和多于一个元素的情况。原因是：删除链表的最后一个元素，实际上便是将倒数第二个元素的next指向None，这一操作必须要保证链表中至少有两个元素。

# 删除表尾元素，并返回其值
# 倒数第一个元素 element.next = None
def pop_last(self):
    if self._head is None:
        raise LinkedListUnderflow('in pop_last')
        
    p = self._head
    if p.next is None:    # 若链表只有一个元素
        e = p.elem
        self._head = None
        return e 
        
    while p.next.next is not None:   # 找链表倒数第二个元素 
        p = p.next
    e = p.next.elem
    p.next = None
    return e

find函数和filter函数

当需要寻找链表中的某一个或某多个元素时，需要从前向后对链表进行遍历，输出相应结果。
find函数可以输出满足要求的第一个元素

# 寻找某一元素 判断谓词**pred**
def find (self, pred):
    p = self._head
    while p is not None:
        if pred(p.elem):
            return p.elem
        p = p.next

判断谓词pred通常由一个判断函数或lambda函数表示：

def pred(elem):
    return (5 > elem)
# 也可以用lambda表达式定制操作参数
pred = lambda elem : elem < 5

上述find函数在找到满足pred要求的第一个元素时，便会停止遍历，返回该元素值。当需要寻找能够链表内满足pred要求的所有函数时，需要利用生成器：

# 筛选生成器
def filter(self, pred):
    p = self._head
    while p is not None:
        if pred(p.elem):
            yield p.elem
        p = p.next

yield关键字可以使返回一个可迭代的 generator（生成器）对象，可以利用next()或者for循环遍历生成器对象来提取结果，这里对于生成器不作过多介绍，实际操作一遍就能明白。

pred = lambda elem : elem < 5
for x in mlist.filter(pred):   # mlist是一个LList类的非空链表结构
    print(x)
# 上述for循环可以输出所有满足pred条件的链表中的元素

element函数

前面在介绍filter函数时介绍了生成器的使用，element函数即是对链表中所有的元素进行输出：

# 生成迭代器
def elements(self):
    p = self._head
    while p is not None:
        yield p.elem
        p = p.next

revs函数——进阶难度

传统的顺序表如list可以通过reverse函数对表中元素进行反转，即将表中元素的顺序进行逆序操作。
对于单链表而言，可以将一个表的首端不断取下结点（首端插入删除结点最为简单，复杂度为O(1))，将其加入到另一个表的首端，这样便完成了一次反转的操作。例如将一摞书一本一本拿下来，放在另一堆。

# 进行反转操作
def revs(self):
	p = None
	while self._head is not None:
		q = self._head
		self._head = q.next       # 摘下原来的首结点
		q._next = p
		p = q                     # 将刚摘下的结点加入p引用的结点序列
	self._head = p                # 反转后的结点序列已经做好，重置表头链接

单向改进链表结构

单向改进链表结构增添了一个属性域_rear，该属性作为另一个指针，可以指向链表的最后一个元素结点，从而使得在尾端添加函数时不需要进行链表遍历。
改进链表结构需注意以下两点：

1. 类定义的内在一致性

前面定义的LList类在判断非空操作时，是根据self._head域进行判断的。在LList1类（改进链表结构）中，

• self._head == None
• self._rear == None

上述两种方法都能进行链表非空判断，但一般需要采用第一种方式，一方面，在同一个类里，不同的方法处理同一事项上应该保持一致，即类定义的内在一致性；另一方面，如果LList1类里判断表空是根据_rear is None来判断， 那么在删除元素时会变得很麻烦，需要时刻关注_rear域，且跟父类不统一。

2. 尾端元素的删除

由于单链表是一个单向结构，在删除最后一个元素时，仍需要从表头开始遍历，这是因为：在删除最后一个元素时，我们需要找的并不是最后一个元素，而是倒数第二个元素，将倒数第二个元素的next值指向None，即可完成尾端元素的删除

其他功能的实现均可根据LList类的对应相关功能进行复写，在这里就不一一赘述，直接上完整的LList1类代码

完整的LList1类代码

# 单链表的简单变形
# 表对象增加一个表尾结点引用域
class LList1(LList):
    def __init__(self):
        LList.__init__(self)
        self._rear = None
    
    def prepend(self, elem):
        # 同一个类里，不同的方法处理同一事项上应该保持一致
        # 如果LList1类里判断表空是根据_rear is None来判断， 那么在删除元素时会变得很麻烦，且跟父类不统一
        # 设计类时，需重点考虑 ** 类设计的内在一致性 **
        if self._head is None:
            self._head = LNode(elem, self._head)
            self._rear = self._head
        else:
            self._head = LNode(elem, self._head)
    
    def append(self, elem):
        if self._head is None:
            self._head = LNode(elem, self._head)
            self._rear = self._head
        else:
            self.rear.next = LNode(elem)
            self._rear = self._rear.next
    
    # pop函数可以不用复写，直接调用
    
    # 由于单链表是一个单向结构，在删除最后一个元素时，仍需要从表头开始遍历
    # 原因： 在删除最后一个元素时，我们需要找的并不是最后一个元素，而是倒数第二个元素
    def pop_last(self):
        if self._head is None:
            raise LinkedListUnderflow('in pop_last')
        
        p = self._head
        
        # 链表只有一个元素
        # p.next is None 等价于 p == self._rear
        if p.next is None:
            e = p.elem
            self._head = None
            # self._rear = None         
            # 该类里判断表空统一用的是self._head
            # 在删除链表里最后一个节点使表变空时，不需要将self._rear赋值为None 
            return e 
        
        while p.next.next is not None:  
            p = p.next
        e = p.next.elem
        p.next = None
        
        self._rear = p   # 删除最后一个元素后，倒数第二个元素变为表尾元素，需加上表尾引用域

        return e

链表相关功能的测试：

mlist = LList1()
mlist.append(1)
print(mlist._head.elem)
print(mlist._rear.elem)
mlist.pop_last()
# print(mlist._head.elem)   # 会报错：AttributeError: 'NoneType' object has no attribute 'elem'
print(mlist._head)
print(mlist._rear.elem)     # 当链表里只有一个元素时，将该元素删除，链表_head会指向None 但_rear仍会指向删除之前的结点

单向循环链表结构

循环链表也是链表的一种变异形式，对于尾端元素，其next值不再指向None，而是指向链表的首端元素。这时，self._head和self._rear从表的内部形态上已无法区分，主要是概念问题。

对于循环链表，需要注意的点是：其只需要一个数据域（采用_rear数据域更方面尾端元素的操作），其在逻辑上始终引用表的尾端结点。
当首端加入结点时，就是在尾结点和首结点之间加入新的首结点，此时尾结点引用不变；当尾端加入结点时，就是在原尾端结点之后（与首端结点之间）插入新的结点，并将新结点作为新的尾端节点。

对于输出链表元素操作，关键在于循环结束的控制。

下面也是直接将完整的LCList类代码附上

完整的LCList类代码

# 循环单链表类
# 只需要一个表尾结点数据域_rear
# 当前端加入结点时，就是在尾结点和首结点之间添加新的首结点
# 当末端加入结点时，就是在现尾结点后添加新的结点，并将其设置为新的尾结点
class LCList():
    def __init__(self):
        self._rear = None
    
    def is_empty(self):
        return (self._rear is None)
    
    # 前端插入新元素
    def prepend(self, elem):     # 这里不能用self.is_empty代替条件
        p = LNode(elem)
        if self._rear is None:
            p.next = p     # 建立一个节点的环
            self._rear = p
        else:
            p.next = self._rear.next      # self._rear.next 代表的是链表的首结点
            self._rear.next = p
    
    # 后端插入新元素
    def append(self, elem):
        self.prepend(elem)
        self._rear = self._rear.next
    
    # 删除元素
    def pop(self):
        if self._rear is None:   
            raise LinkedListUnderflow('in pop')
        
        p = self._rear.next    # 即链表首结点
        if self._rear is p:
            self._rear = None
        else:
            self._rear.next = p.next
        
        return p.elem
    
    # 删除尾端元素
    def pop_last(self):
        if self._rear is None:
            raise LinkedListUnderflow('in pop')
        
        p = self._rear.next
        while p.next is not self._rear:
            p = p.next         # 寻找链表中倒数第二个元素

        p.next = self._rear.next
        self._rear = p
        
    def printall(self):
        if self.is_empty():
            return
        
        p = self._rear.next
        while True:
            print(p.elem)
            if p is self._rear:
                break
            p = p.next

双向简单链表结构

双向链表中的每一个元素结点除了能够链接其后驱结点，同时也能链接其前继结点，使得链表元素的增加与删除操作变得更加复杂。

在完善双向链表的功能时，首先完成其定义：

# 双向链表类
class DLList(LList1):
    def __init__(self):
        LList1.__init__(self)

在添加新元素结点时，需建立新元素和其前后元素的双向链接，建立方法是判断新结点与其附近已有结点的前后关系

prepend函数

要在链表首端前添加新元素，则新元素的next_属性是指向原链表的self._head，同时要将原链表的首端结点与新结点建立prev关系。

# 前端插入新元素
def prepend(self, elem):
    p = DLNode(elem, None, self._head)
    if self._head is None:
        self._rear = p
    else:
        p.next.prev = p    # 建立后一元素和前一元素的前向链接

    self._head = p

append函数

append函数同理

# 后端插入新元素
def append(self, elem):
    p = DLNode(elem, self._rear, None)
    if self._head is None:
        self._head = p
    else:
        p.prev.next = p   # 建立前一元素和后一元素的链接
    self._rear = p

pop和pop_last等函数在进行定义时也有些许差别，具体可见完整的DLList类代码

完整的DLList类代码

# 双向链表类
class DLList(LList1):
    def __init__(self):
        LList1.__init__(self)
    
    # 添加新元素时，需建立新元素和其前后元素的双向链接
    # 建立方法：判断新元素和已有元素的前后关系 
    # 前端插入新元素
    def prepend(self, elem):
        p = DLNode(elem, None, self._head)
        if self._head is None:
            self._rear = p
        else:
            p.next.prev = p    # 建立后一元素和前一元素的前向链接

        self._head = p
    
    # 后端插入新元素
    def append(self, elem):
        p = DLNode(elem, self._rear, None)
        if self._head is None:
            self._head = p
        else:
            p.prev.next = p   # 建立前一元素和后一元素的链接
    
        
        self._rear = p
    
    def pop(self):
        if self._head is None:
            raise LinkedListUnderflow('in pop of DLList')
        
        e = self._head.elem
        self._head = self._head.next   # 删除前端元素
        if self._head is not None: 
            self._head.prev = None
        # 若删除完链表变为空表，可以不进行任何操作。
        # if self._head is None:
        #     self._rear = None
        # else:
        #     self._head.prev = None
        
        return e
    
    def pop_last(self):
        if self._head is None:          # 这里的判别条件就不能是self._rear 因为当有一个元素的链表删除元素后， self._rear不为None
            raise LinkedListUnderflow('in pop_last of DLList')
        
        e = self._rear.elem
        self._rear = self._rear.prev

        if self._rear is None:
            self._head = None           # 防止表空判断出现问题
        else:
            self._rear.next = None
        
        return e

双向循环链表结构

双链表也可以采用循环链表的结构，将尾端结点的next域指向表的首端结点，并将首端结点的prev域指向尾端结点。在这种结构中，各结点的next引用形成了向下一结点的引用换，而prev引用形成了向前一结点方向的引用换。因此，可以将尾端结点的指针取消掉。
完整的DLCList类代码如下所示：

# 双向循环链表类
# 由于prev属性的存在，尾结点指针并不必要
class DLCList(LList):
    def __init__(self):
        LList.__init__(self)
    
    def is_empty(self):
        return (self._head is None)
    
    # 前端插入新元素
    def prepend(self, elem):
        p = DLNode(elem)
        if self._head is None:
            self._head = p
            p.next = p
            p.prev = p
        else:
            cur = self._head
            # 寻找尾结点
            while cur.next is not self._head:
                cur = cur.next
            
            # 将新结点与前端结点建立联系
            p.next = self._head
            self._head.prev = p

            self._head = p

            # 将新结点与尾端结点建立联系
            cur.next = self._head
            self._head.prev = cur
    
    # 末端插入新元素
    def append(self, elem):
        p = DLNode(elem)

        if self._head is None:
            self._head = p
            p.next = p
        else:
            cur = self._head
            # 寻找尾结点
            while cur.next is not self._head:
                cur = cur.next
            
            cur.next = p
            p.prev = cur

            p.next = self._head
            self._head.prev = p
    
    # 删除前端元素
    def pop(self):
        if self._head is None:
            raise LinkedListUnderflow('in pop of DLCList')
        
        p = self._head
        if p.next is self._head:    # 链表中仅有一个元素
            self._head = None
        else:
            self._head.next.prev = self._head.prev
            self._head.prev.next = self._head.next
            
            self._head = self._head.next

        return p.elem
    
    def printall(self):
        p = self._head

        while p.next is not self._head:
            print(p.elem, end='')
            print(', ', end='')

            p = p.next
            
        print(p.elem, end='')

总结

总而言之，链表这一结构能够将表元素储存在一批较小的存储块里，通过显式链接形成一种链式结构，直接反映元素的顺序关系。
链表实现的灵活性较强，操作的实现方式更加灵活多样，但其元素不能随机访问，按位置访问的代价极高。对于一个链表，能直接掌握的只有首结点（以及可能的尾结点，这需要额外的存储空间代价），只能顺着链接结构一步一步去查找。

为了突破简单链表的操作限制，可以通过增加尾端结点指针域、双向结构建立循环连接等对链表进行变形，但这些不仅需要付出存储的代价，同时也给操作的实现带来新的问题，如尾指针的维护、前向链接的维护等。