2017-2018 ACM-ICPC, Asia Tsukuba Regional Contest(部分题解)
传送门
2017-2018 ACM-ICPC 日本筑波区域赛
Problem A:Secret of Chocolate Poles
思路:简单dp。 d [ i ] [ 0 / 1 ] d[i][0/1] d[i][0/1]表示高度为i时,顶层圆盘是0/1颜色时的方案数。
#include
using namespace std;
typedef long long ll;
ll d[110][2];
int main()
{
int n,k;
cin>>n>>k;
memset(d,0,sizeof d);
d[0][0]=1;
for(int i=1;i<=n;i++)
{
d[i][0]+=d[i-1][1];
d[i][1]+=d[i-1][0];
if(i>=k)d[i][1]+=d[i-k][0];
}
ll ans=0;
for(int i=1;i<=n;i++)ans+=d[i][1];
cout< Problem B:Parallel Lines
思路:首先预处理出子集 f [ i ] [ j ] f[i][j] f[i][j],表示线段集合为 i i i且集合中有一条线段为 j j j时,这个子集里面的所有线段之间互相平行的对数。
然后状压枚举子集求答案。
理论上最高的复杂度为 O ( 2 n ∗ 12 0 2 + 3 n ) O(2^n*120^2+3^n) O(2n∗1202+3n),但实际上预处理的过程中有许多无效状态。
#include
using namespace std;
typedef long long ll;
struct Point{int x,y;}p[20],tp[125];
Point operator-(Point A,Point B){return (Point){A.x-B.x,A.y-B.y};}
int operator^(Point A,Point B){return A.x*B.y-A.y*B.x;}
int f[1<<16][125];
int ans[1<<16];
int main()
{
int n;
cin>>n;
for(int i=0;i Problem C:Medical Checkup
思路:推一下,可以发现一个人的h值影响着以后的人的检查时间,每一个人依次检查完设备的时间是一个等差数列,注意t=0的情况。(用二分可以避免)
#include
using namespace std;
const int MAX=1e5+10;
typedef long long ll;
ll h[MAX];
int main()
{
ll n,t;
cin>>n>>t;
for(int i=1;i<=n;i++)scanf("%lld",&h[i]);
ll sum=0;
for(int i=1;i<=n;i++)
{
sum+=h[i];
ll d=max(h[i],h[i-1]);
ll l=1,r=1e9+10,ans=1;
while(r>=l)
{
ll m=(l+r)/2;
if(sum+d*(m-1)>t)
{
r=m-1;
ans=m;
}
else l=m+1;
}
h[i]=d;
printf("%lld\n",ans);
}
return 0;
}
Problem E:Black or White
思路:DP。 d [ i ] d[i] d[i]表示前 i i i个格子已经涂好了的最小次数,那么 d [ i ] = m i n ( d [ j ] + c o s t [ j + 1 , i ] ) , ( j + k > = i ) d[i]=min(d[j]+cost[j+1,i]),(j+k>=i) d[i]=min(d[j]+cost[j+1,i]),(j+k>=i)对于 c o s t [ j + 1 , i ] cost[j+1,i] cost[j+1,i]可以发现,若这个区间有 x x x个连续的颜色段,那么最少次数为 x 2 + 1 \frac x2+1 2x+1
其中 c o s t [ j + 1 , i ] cost[j+1,i] cost[j+1,i]可以预处理出来,转移方程就需要用单调递增的队列来优化了。
d [ i ] = m i n ( d [ j ] + c o s t [ i ] − c o s t [ j ] 2 + 1 ) d[i]=min(d[j]+\frac{cost[i]-cost[j]}{2}+1) d[i]=min(d[j]+2cost[i]−cost[j]+1) 2 ∗ d [ i ] = m i n ( 2 ∗ d [ j ] − c o s t [ j ] + c o s t [ i ] + 2 ) 2*d[i]=min(2*d[j]-cost[j]+cost[i]+2) 2∗d[i]=min(2∗d[j]−cost[j]+cost[i]+2)
#include
using namespace std;
const int MAX=5e5+10;
typedef long long ll;
char a[MAX],b[MAX];
int sum[MAX],d[MAX];
deque >p;
int main()
{
memset(d,0,sizeof d);
memset(sum,0,sizeof sum);
int n,k;
cin>>n>>k;
scanf("%s%s",a+1,b+1);
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+(b[i]!=b[i-1]);
p.push_front({0,0});
for(int i=1;i<=n;i++)
{
while(!p.empty()&&p.back().first+k=2*d[i]-sum[i])p.pop_front();
p.push_front({i,2*d[i]-sum[i]});
}
cout< Problem F:Pizza Delivery
思路:预处理出 d [ i ] d[i] d[i]和 f [ i ] f[i] f[i], d [ i ] d[i] d[i]表示沿有向边的正方向从点1到 i i i点的最短距离, f [ i ] f[i] f[i]表示沿有向边的反方向点2到 i i i点的最短距离。
我们首先可以求出一个从点1到点2的所有最短路经过的边构成的DGA。
对于第 i i i条边,如果 d [ b ] + f [ a ] + c < d [ 2 ] d[b]+f[a]+c<d[2] d[b]+f[a]+c<d[2],那么输出明显是"HAPPY";否则,看这条边是否是上述DGA中的桥,如果是就是"SAD",否则就不会改变这个DGA的连通性,也就不会改变最短路,输出"SOSO"。
#include
using namespace std;
const int MAX=2e5+10;
typedef long long ll;
struct lenka{int x,y,z,index;}a[MAX];
struct EDG{int to,next,cost,dir;}ed[MAX];
int head[MAX],tot=0;
void add(int x,int y,int z,int dir)
{
ed[tot].to=y;
ed[tot].cost=z;
ed[tot].dir=dir;
ed[tot].next=head[x];
head[x]=tot++;
}
priority_queue,vector >,greater > >p;
void BFS(ll *d,int st,int dir) //求最短路
{
d[st]=0;
p.push({0,st});
while(!p.empty())
{
pairnow=p.top();p.pop();
if(now.first!=d[now.second])continue;
for(int i=head[now.second];i!=-1;i=ed[i].next)
{
if(ed[i].dir!=dir)continue;
int nex=ed[i].to;
if(d[nex]==-1||d[nex]>now.first+ed[i].cost)
{
d[nex]=now.first+ed[i].cost;
p.push({d[nex],nex});
}
}
}
}
ll d[MAX],f[MAX];
int low[MAX],pre[MAX],v[MAX],dfs_clock=0;
vector >e[MAX];
void dfs(int k,int fa) //找出DGA中的桥
{
low[k]=pre[k]=++dfs_clock;
for(int i=0;inex=e[k][i];
if(pre[nex.first]==0)
{
dfs(nex.first,nex.second);
low[k]=min(low[k],low[nex.first]);
if(low[nex.first]>pre[k])v[nex.second]=1;
}
else if(nex.second!=fa)low[k]=min(low[k],pre[nex.first]);
}
}
int main()
{
int n,m;
cin>>n>>m;
memset(head,-1,sizeof head);
for(int i=1;i<=m;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z,1);
add(y,x,z,0);
a[i]=(lenka){x,y,z,i};
}
memset(d,-1,sizeof d);
memset(f,-1,sizeof f);
BFS(d,1,1);
BFS(f,2,0);
for(int i=1;i<=m;i++)
{
if(d[a[i].x]==-1||f[a[i].y]==-1)continue;
if(d[a[i].x]+f[a[i].y]+a[i].z==d[2])
{
e[a[i].x].push_back({a[i].y,a[i].index});
e[a[i].y].push_back({a[i].x,a[i].index});
}
}
dfs(1,0);
for(int i=1;i<=m;i++)
{
if(d[a[i].y]!=-1&&f[a[i].x]!=-1&&d[a[i].y]+f[a[i].x]+a[i].z Problem G:Rendezvous on a Tetrahedron
思路:在三维坐标系下计算很复杂,可以把这个正四面体各个面展开平铺在二维平面上并向四周扩展。此时只需找出终点在哪个正三角行内即可。
如下图
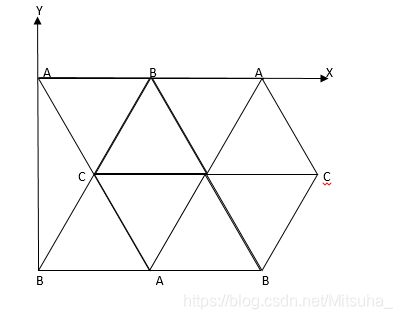
扩展开来发现这些三角形是有规律的,只要找出终点在哪一行的哪个三角形里,就可以求解。
#include
using namespace std;
const int MAX=2e9+10;
const double PI=acos(-1.0);
typedef long long ll;
struct Point{double x,y;};
Point operator+(Point A,Point B){return (Point){A.x+B.x,A.y+B.y};} //向量A+B
Point operator-(Point A,Point B){return (Point){A.x-B.x,A.y-B.y};} //向量A-B
Point operator*(Point A,double B){return (Point){A.x*B,A.y*B};} //向量A*B
Point operator/(Point A,double B){return (Point){A.x/B,A.y/B};} //向量A/B
double abs(Point A){return sqrt(A.x*A.x+A.y*A.y);} //向量A的长度
double operator*(Point A,Point B){return A.x*B.x+A.y*B.y;} //向量A B的点积
double operator^(Point A,Point B){return A.x*B.y-A.y*B.x;} //向量A B的叉积
double cross(Point A,Point B){return A.x*B.y-A.y*B.x;} //向量A B的叉积
double dis(Point A,Point B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}//A B两点的距离
double dis2(Point A,Point B){return (A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y);} //A B两点的距离的平方
Point cal(Point st,Point A,Point B,int degree)
{
double l=0,r=1;
Point m;
for(int i=1;i<=200;i++)
{
m=((B-A)*(l+r)/2)+A;
//m.show();
double angle=((B-st)*(m-st))/(abs(B-st)*abs(m-st));
angle=acos(angle)*180/PI;
if(angle-degree>1e-6)l=(l+r)/2;
else r=(l+r)/2;
}
return m-st;
}
string solve(string edg,int degree,int L)
{
Point v=cal({0,0},{1.0,-sqrt(3)},{2.0,0},degree);//求出速度矢量
v=v/abs(v)*L; //求出终点
int y=0;
while((y+1)*sqrt(3)/2+v.y<0)y++;//求出v在第几行的正三角形里面
if(y%4==0||y%4==2)
{
Point A={0,-y*sqrt(3)/2};
Point B={0.5,-(y+1)*sqrt(3)/2};
for(int i=1;;i++) //找出v是第几个正三角形
{
if(cross(A-v,B-v)<0)
{
if(y%4==0)
{
if(i%4==1)return "ACD";
if(i%4==2)return "ABC";
if(i%4==3)return "BCD";
if(i%4==0)return "ABD";
}
else
{
if(i%4==1)return "BCD";
if(i%4==2)return "ABD";
if(i%4==3)return "ACD";
if(i%4==0)return "ABC";
}
}
if(i%2)A.x+=1;
else B.x+=1;
}
}
if(y%4==1||y%4==3)
{
Point A={0.5,-y*sqrt(3)/2};
Point B={0,-(y+1)*sqrt(3)/2};
for(int i=1;;i++) //找出v是第几个正三角形
{
if(cross(A-v,B-v)<0)
{
if(y%4==1)
{
if(i%4==1)return "BCD";
if(i%4==2)return "ABC";
if(i%4==3)return "ACD";
if(i%4==0)return "ABD";
}
else
{
if(i%4==1)return "ACD";
if(i%4==2)return "ABD";
if(i%4==3)return "BCD";
if(i%4==0)return "ABC";
}
}
if(i%2)B.x+=1;
else A.x+=1;
}
}
}
mapma;
int main()
{
ma['A']='A';
string edg;
int degree,L;
cin>>edg>>degree>>L;
for(int i=0;i<=1;i++)ma['B'+i]=edg[i];//因为初始出发的方向不同,把点替换成相应的点
ma['D']='B'+'C'+'D'-edg[0]-edg[1];
string A=solve(edg,degree,L);
for(int i=0;i<=2;i++)A[i]=ma[A[i]];
cin>>edg>>degree>>L;
for(int i=0;i<=1;i++)ma['B'+i]=edg[i];
ma['D']='B'+'C'+'D'-edg[0]-edg[1];
string B=solve(edg,degree,L);
for(int i=0;i<=2;i++)B[i]=ma[B[i]];
sort(A.begin(),A.end());
sort(B.begin(),B.end());
puts(A==B?"YES":"NO");
return 0;
}
Problem I:Starting a Scenic Railroad Service
思路:第一种情况的答案就是对于所有线段,与其有公共区间的线段数量的最大值。
求与一条线段有公共区间的线段数量,对所有线段按左端点排序,二分求出所有左端点在该线段里的线段数量,然后再用主席树求出右端点在该线段里的线段数量,累加即是答案。
第二种情况用差分,然后累加和的最大值就是答案。
#include
using namespace std;
const int MAX=2e5+10;
typedef long long ll;
vectorv;
struct lenka
{
int L,R,sum;
}A[MAX*40];
int tot,root[MAX],a[MAX];
void init()
{
tot=1;
root[0]=0;
A[0].L=A[0].R=A[0].sum=0;
}
void build(int x,int&rt,int l,int r)
{
A[tot++]=A[rt];
rt=tot-1;
A[rt].sum++;
if(l==r)return;
if(x<=(l+r)/2)build(x,A[rt].L,l,(l+r)/2);
else build(x,A[rt].R,(l+r)/2+1,r);
}
int ask(int l,int r,int x,int y,int k)
{
if(l==r)return A[y].sum-A[x].sum;
if(k>(l+r)/2)return ask((l+r)/2+1,r,A[x].R,A[y].R,k);
return A[A[y].R].sum-A[A[x].R].sum+ask(l,(l+r)/2,A[x].L,A[y].L,k);
}
int getid(int x){return lower_bound(v.begin(),v.end(),x)-v.begin()+1;}
struct Point{int x,y;}p[MAX],B[MAX];
int cmpx(const Point&x,const Point& y)
{
if(x.x==y.x)return x.y=l)
{
int m=(l+r)/2;
if(B[m].x>n;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&p[i].x,&p[i].y);
sum[p[i].x]++;
sum[p[i].y]--;
}
for(int i=1;i<=n;i++)B[i]=p[i];
sort(B+1,B+n+1,cmpx);
init();
for(int i=1;i<=n;i++)v.push_back(B[i].y);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=n;i++)
{
root[i]=root[i-1];
build(getid(B[i].y),root[i],1,n);
}
int ans=0;
for(int i=1;i<=n;i++)
{
int R=f(p[i].y);
int L=f(p[i].x);
ans=max(ans,max(0,R-L)+ask(1,n,root[0],root[L],getid(p[i].x+1)));
}
for(int i=1;i<=100000;i++)sum[i]+=sum[i-1];
printf("%d %d\n",ans,*max_element(sum+1,sum+100001));
return 0;
}