LeNet网络（1989年提出,1998年改进）

LeNet网络（1989年提出,1998年改进）

1.LeNet网络简介

LeNet:

LeNet卷积神经网络的雏形：1989年，LeCun等人设计了用于手写邮政编码的卷积神经网络，并使用反向传播算法训练卷积神经网络，将其应用与美国邮政服务。

性能：LeNet网络性能优异，在邮政编码数字数据集上的测试结果显示，该网络错误率仅为1%。

限制：由于当时计算机硬件能力限制，卷积神经网络规模无法进一步增大，制约了其在更复杂任务以及更大数据集上的发展，没有引起广泛关注

LeNet-5网络：卷积神经网络的经典之作和开山之作、先驱。

应用：最先被用于处理计算机视觉的问题，在识别手写体数字的准确性上取得了非常好的成绩。

发展：1998年出现改进版本LeNet-5。

1998年论文：《Gradient-Based Learning Applied to Document Recognition》——Yann LeCun等

主要用于手写字符的识别。

地位：层数较少，包含卷积层、池化层、全连接层等深度神经网络的基本模块，可以作为学习其他深度网络模型的基础。

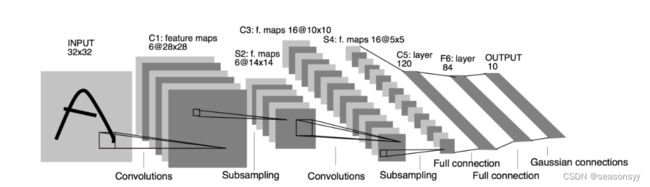
LeNet-5网络结构如图0所示

图0

LeNet-5网络从左往右分别是INPUT层、C1层、S2层、C3层、S4层、C5层、F6层和OUTPUT层。

一共包括输入层、两个卷积层(Convolutions)、两个池化层(Pooling/ 下采样层 Subsampling)、三个全连接层(Full connection)。

它的输入是一个32× 32× 1的灰度图像；输出则有10个分类，分别代表10个手写字符0~9

接下来分层介绍：

（1）INPUT层（输入层）

默认输入数据必须是一个32× 32× 1的灰度图像，即高度和宽度均为32的单色彩通道图像。

实际上，输入图像原始大小为28×28像素，其中的字符大小不超过20× 20像素，此处将输入图像补全至32× 32像素，以确保经过卷积层后，图像中位于边缘的信息不会丢失。

（2）C1层（第一个卷积层）

使用的卷积滑动窗口大小为5× 5× 1，步长为1，不使用Padding（填充）。

套用卷积通用公式：
$$output=[(input-filterSize+2\ast padding)/stride]+1$$
输出特征图的高度和宽度为28=[(32-5+2*0)/1]+1

同时在图0中可以看到，这个卷积层最后要求的深度输出深度为6的特征图，因此需要进行6次同样的卷积操作（6个卷积核），最后得到的输出特征图的维度为28× 28×6.

经过了一层卷积，图像尺寸变小了，但是深度却增加了

（3）S2层（第一个池化层/下采样层/汇聚层）

下采样层的功能：缩减输入特征图的大小，这里使用最大汇聚层进行下采样

输入特征图的维度为28× 28×6.

S2层采样方式比较特殊，包含可学习的参数。形式上看更类似于卷积核尺寸为2*2，步长为2的不重叠卷积。

不同的是，其输出为：

对于2×2内的4个输入数据xi，首先求和，然后乘以一个可训练参数w，再加上一个可训练偏置b，得到的结果通过Sigmoid函数进行激活。

由于输入为6通道数据，所以S2层有6个可学习的运算核，共12个可学习的参数。

并且，S2层实质上包含了激活层，采用的激活函数为Sigmoid函数。

输出特征图尺寸：[(28-2+2×0)/2]+1=14

最后得到的输出特征图的维度为14× 14×6.

在这篇论文写成的年代，人们普遍喜欢用平均池化方法，所以LeNet-5网络的所有池化操作都采取平均池化。

注：池化操作不改变特征图的深度，即通道数不会变

（4）C3层（第二个卷积层）

卷积核：5×5×6，因为输入特征图的维度为14 ×14×6，所以卷积核窗口的深度必须和输入特征图深度一致。

步长为1，不使用Padding。

输出特征图大小：[（14-5+2×0）/1]+1=10

同时，这个卷积层要求最后输出深度为16的特征图，因此需要进行16次卷积，最后得到的输出特征图的维度为

10× 10×16

（5）S4层（第二个池化层/下采样层/汇聚层）

输入特征图是C3输出的维度为10× 10×16的特征图

滑动窗口大小2× 2×16，步长为2

输出特征图的高度和宽度：[（10-2+2×0）/2]+1=5

最后输出的特征图维度为5×5×16

（6）C5层（第一个全连接层）

是卷积池化层和后面的全连接层的第一个中间层/隐含层，可以看做第3个卷积层，由120个神经元组成，激活函数采用Tanh或Sigmoid函数

输入的特征图维度为5×5×16

卷积核滑动窗口大小：5×5×16，步长为1，不使用Padding。

最后输出的特征图的高度和宽度：[(5-5+2×0)/1]+1=1

同时这个卷积层要求最后输出的深度为120的特征图，因此需要进行120次卷积，最后得到的输出特征图的维度为1×1×120，实际上实现了二维数据的展平。

（7）F6层(第二个全连接层)

是卷积池化层和后面的全连接层的第二个中间层/隐含层。由84个神经元构成，激活函数与上一层相同，Tanh或Sigmoid函数

输入数据数据是维度为1×1×120的特征图。

最后要求输出深度为84的特征图，因此本层任务就是对输入特征图进行压缩，最后得到维度为 1×84的特征图。

要完成这个过程，需要让输入特征图乘以一个维度为120×84的权重参数。

根据矩阵运算规则：[1×120]×[120× 84]=[1×84]

输出节点数为84:，之所以选择84，是因为将特征图映射到7×12=84大小的ASCII码比特图像中。

每个图像中，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应与一个编码。

输出特征图：维度为1×84的矩阵

（8）OUTPUT层（输出层/全连接层）

output层也是全连接层，共有10个节点，分别代表数字0~9

因为LeNet-5是用来解决分类问题的，所以需要根据输入图判断图像中手写数字的类别，输出的结果是输入图像对应10个类别的可能性。

在此之前，需要先将F6层输入的维度为184的数据压缩成维度为1×10的数据，依靠一个维度为84× 10的矩阵完成。（output层有8410=840个参数和连接）

[1×84]×[84× 10]=[1×10]

将最终得到的10个数据全部输入Softmax激活函数中，得到的就是模型预测的输入图像所对应的10个类别的可能性值。

总结LeNet-5网络结构：

（1）C1层使用6个5×5卷积核，做步长为1的卷积，激活函数使用Tanh或Sigmoid函数，且有偏值。

（2）S2层做2×2的平均池化

（3）C3层使用16个5×5卷积核，做步长为1的卷积，激活函数使用Tanh或Sigmoid函数，且有偏值。

（4）S4层做2×2的平均池化

（5）C5层有120个神经元，激活函数使用Tanh或Sigmoid函数，且有偏值。

（6）F6层有84个神经元，Tanh或Sigmoid函数，且有偏值。

（7）分类器有10个分类输出

layer_name	input	kernel_size	kernel_num	stride	padding	output
C1层（卷积层）	32× 32×1	5×5	6	1	0	[(32-5+2×0)/1]+1=28 28×28×6
S2层（池化层）	28*28×6	2×2	6	2	0	[(28-2+2×0)/2]+1=14 14× 14×6
C3层（卷积层）	14× 14×6	5×5	16	1	0	[（14-5+2×0）/1]+1=10 10× 10×16
S4层（池化层）	10× 10×16	2×2	16	2	0	[（10-2+2×0）/2]+1=5 5×5×16
C5层（全连接层）	5×5×16	5×5	16	1	0	[(5-5+2×0)/1]+1=1 1×1×120
F6层（全连接层）	1×1×120					[1×120]×[120× 84]=[1× 84] 1×84
output层（全连接层）	1×84					[1×84]×[84× 10]=[1× 10] 1×10

2.LeNet网络代码讲解

图像分类篇：pytorch官方demo代码讲解

参考：

b站博主@霹雳吧啦Wz：https://space.bilibili.com/18161609/channel/index

github:https://gitcode.net/mirrors/wzmiaomiao/deep-learning-for-image-processing?utm_source=csdn_github_accelerator

代码位置：\deep-learning-for-image-processing-master\pytorch_classification\Test1_official_demo

用到了pytorch官网对应代码：https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html

这节课主要内容：

• 讲解LeNet网络的模型
• 通过pytorch搭建了LeNet的模型
• 介绍了CIFAR10数据集，下载了数据集，对数据集进行了预处理
• 查看了数据集，导入LeNet模型
• 定义了损失函数、优化器
• 进行网络的训练，并将训练好的权重保存
• 通过pridect.py脚本调用保存好的模型权重进行预测

Pytorch Tenor的通道排序：[batch ,channel,height,width]

讲解的LeNet-5网络示意图，如图0

图0

讲解页面：model.py

import torch.nn as nn
import torch.nn.functional as F


class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        #输入图像矩阵深度=3，输出图像矩阵深度/卷积核个数=16，卷积核大小5*5
        self.conv1 = nn.Conv2d(3, 16, 5)
        self.pool1 = nn.MaxPool2d(2, 2)#池化核2*2，步长=2
          #输入图像矩阵深度=16（因为第一个卷积层输出矩阵深度为16，池化层不改变图像深度），输出图像矩阵深度/卷积核个数=32，卷积核大小5*5
        self.conv2 = nn.Conv2d(16, 32, 5)
        self.pool2 = nn.MaxPool2d(2, 2)#池化核2*2，步长=2
        #全连接层 全连接层的输入是一个一维的向量，所以需要将得到的特征矩阵展平，展成一个一维的向量。
        #图0中这一层的结点个数是120，所以第二个参数是120（120这个参数是自定义的）
        self.fc1 = nn.Linear(32*5*5, 120)
        #第二个全连接层的输入是第一个全连接层的输出：120个节点。
        #图0中这一层设置的是84个节点，所以第二个参数是84（84这个参数是自定义的）
        self.fc2 = nn.Linear(120, 84)
        #最后一个全连接层的输入是上一层的输出：84个节点
        #输出需要根据训练集来进行修改，因为今天使用的训练集是有10个类别的，所以第二个参数设置成10
        self.fc3 = nn.Linear(84, 10)

        #正向传播过程
        #x代表输入的数据，数据就是pytorch Tensor的通道顺序：[batch,channel,height,width]
    def forward(self, x):
      #首先数据经过卷积层1(conv1)，然后得到的输出通过relu激活函数
        x = F.relu(self.conv1(x))    # input(3, 32, 32) output(16, 28, 28)
        #然后再将上面的输出经过下采样一层（pool1）
        x = self.pool1(x)            # output(16, 14, 14)
        #将上面的输出进入到第二个卷积层（conv2），然后得到的输出通过relu激活函数
        x = F.relu(self.conv2(x))    # output(32, 10, 10)
        #然后再将输出通过第二个下采样层（pool2）
        x = self.pool2(x)            # output(32, 5, 5)
        #接下来要把数据放到全连接层中，但是全连接层的输入是一维向量。所以要把现在的向量展平成一维向量
        #做法：使用.view函数展平向量，第一个参数-1代表第一个维度，进行自动推理（因为第一维是batch，所以设置成-1）第二个维度是展平后的节点的个数32*5*5
        x = x.view(-1, 32*5*5)       # output(32*5*5)
        #全连接层1，如图0中，自定义了120个节点，所以第一个全连接层的输出是120
        x = F.relu(self.fc1(x))      # output(120)
        #全连接层2，自定义了输出是84个节点
        x = F.relu(self.fc2(x))      # output(84)
        #全连接层3，自定义了输出是10个节点
        #输出需要根据训练集来进行修改，因为今天使用的训练集是有10个类别的，所以第二个参数设置成10
        x = self.fc3(x)              # output(10)
        #为什么这里没有用softmax层（对于一般分类问题最后一个全连接层会跟上一个softmax层，将输出转化成为一个概率分布，理论上确实应该这么做，但是在我们训练网络过程中，计算卷积交叉熵的过程中已经实现了一个更加高效的softmax方法，所以在这里不需要添加softmax层了）
        return x

在pytorch中搭建模型流程：

1. 新建一个类LeNet，这个类继承自nn.Module这个父类

2. 在这个类中实现两个方法：

• 一个是初始化函数：def__ init__(self)

• 初始化函数中会实现在搭建网络过程中所使用的一些网络层结构

• 首先使用super这个函数，（只要涉及到多继承，都会使用super这个函数）

• 1. 定义第一个卷积层：在pytorch中定义卷积层用 nn.Conv2d函数

  ctrl点入Conv2d中去：

  def __init__(
      self,
      in_channels: int, #输入图像矩阵的深度（RGB就是3）
      out_channels: int,#输出特征矩阵的深度=卷积核的个数
      kernel_size: _size_1_t,#卷积核的大小
      stride: _size_1_t = 1,#步长，默认为1
      padding: Union[str, _size_1_t] = 0,#在四周进行补0处理，默认=0
      dilation: _size_1_t = 1,#高阶用法
      groups: int = 1,#高阶用法
      bias: bool = True,#偏执，默认使用=True
      padding_mode: str = 'zeros',  # TODO: refine this type
      device=None,
      dtype=None
  ) 
  

经卷积后的矩阵尺寸大小计算公式为：N=(W-F+2P)/S+1

• 输入图片大小W×W
• Filter大小F×F(卷积核大小)
• 步长S
• padding的像素数P

所以第一个卷积层的输出计算：

• 输入大小为：32×32，卷积核大小为5×5，步长默认=1，padding默认=0.
• 使用公式计算得出N=28.即输出图像的大小为28×28
• 输出图像的深度=卷积核的个数=16
• 所以输出图像尺寸为：16× 28× 28

• 2. 定义下采样层：pool1。使用的方法：nn.MaxPool2d

  ctrl点入MaxPool2d中去：

  class _MaxPoolNd(Module):
      __constants__ = ['kernel_size', 'stride', 'padding', 'dilation',
                       'return_indices', 'ceil_mode']
      return_indices: bool
      ceil_mode: bool
  
      def __init__(self,
                   kernel_size: _size_any_t,
                   stride: Optional[_size_any_t] = None,
                   padding: _size_any_t = 0, dilation: _size_any_t = 1,
                   return_indices: bool = False, ceil_mode: bool = False) -> None:
          super().__init__()
          self.kernel_size = kernel_size
          #stride步长指定或者步长=卷积核大小
          self.stride = stride if (stride is not None) else kernel_size
          self.padding = padding
          self.dilation = dilation
          self.return_indices = return_indices
          self.ceil_mode = ceil_mode
  
  

  因为池化只改变特征矩阵的宽和高，不改变channel

  所以池化层之后的输出矩阵深度=16（前一个卷积层的输出作为这个池化层的输入）

  步长=2，所以输出的图像大小缩小为输入的一半，输入是28× 28，所以输出时14× 14

• 3. 定义第二个卷积层：conv2。使用nn.Conv2d函数。
• 4. 定义第二个池化层：pool2。使用nn.MaxPool2d函数。

• 一个是forward函数中定义正向传播的过程：def forward(self, x)

当我们实例化这个类之后，将参数传入到实例中就会进行正向传播（也就是按照forward这个顺序进行运行）

讲解页面：train.py层

def main():
    # transform这个函数首先通过transforms.Compose这个函数将所要使用的一些预处理方法给打包成为一个整体
    # 在这里使用了两个预处理方法：
    # 第一个是ToTensor，ctrl点进去看具体功能
    transform = transforms.Compose(
        [transforms.ToTensor(),
         transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

ToTensor函数ctrl点进去：

class ToTensor:
 #这是一个把PIL图像或者ndarray转化成tensor的函数
 """Convert a PIL Image or ndarray to tensor and scale the values accordingly.
 This transform does not support torchscript.
# 导入的图片不管是通过PIL导入还是通过ndarray导入，所显示的数据图像的顺序是高度Height*宽度#Width*通道数/深度Channels。每个维度的像素值范围都是0-255
 Converts a PIL Image or numpy.ndarray (H x W x C) in the range
 [0, 255] to a torch.
 #通过ToSensor这个函数把shape变成了通道数/深度Channels*高度Height*宽度#Width。
 #并且将每个维度的像素值范围从0-255变成了0-1
 FloatTensor of shape (C x H x W) in the range [0.0, 1.0]
 if the PIL Image belongs to one of the modes (L, LA, P, I, F, RGB, YCbCr, RGBA, CMYK, 1)

总结：Tensor作用：

原来输入图像的通道顺序是高度Height×宽度#Width*深度Channels。且每个维度的像素值范围都是0-255

通过ToSensor这个函数把shape变成了深度Channels × 高度Height× 宽度Width。
并且将每个维度的像素值范围从0-255变成了0-1

Normalize函数ctrl点进去：

class Normalize(torch.nn.Module):
#使用均值和标准差来标准化我们的tensor
#计算过程：输出=（原始数据-均值）/标准差
 """Normalize a tensor image with mean and standard deviation.
 This transform does not support PIL Image.
 #提供的参数有均值mean，标准差std
 #这个模型将会标准化每个输入的通道
 Given mean: ``(mean[1],...,mean[n])`` and std: ``(std[1],..,std[n])`` for ``n``
 channels, this transform will normalize each channel of the input
 ``torch.*Tensor`` i.e.,
 #计算过程：输出=（原始数据-均值）/标准差
 ``output[channel] = (input[channel] - mean[channel]) / std[channel]``

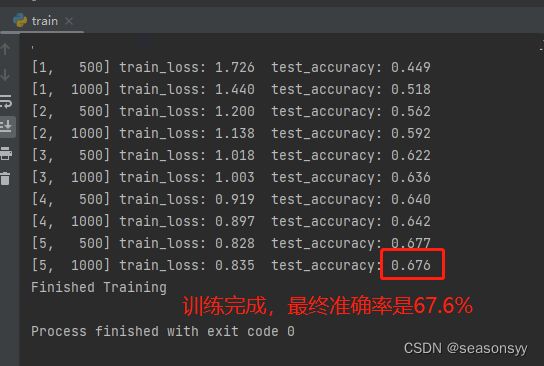
运行train.py页面，结果如图1

图1

训练完之后在目前的根目录下生成了一个模型权重文件：Lenet.pth，如图2

图2

然后在网上下载一张飞机的图片，放到目前项目的根目录中。

打开predict.py文件，这个文件就是调用模型权重进行预测的脚本

运行完之后，得到结果，如图3

图3

3.参考文献

1.《深度学习与神经网络》 赵眸光 编著

出版社：电子工业出版社 2023年1月第一版

ISBN: 978-7-121-44429-6

2.《深度卷积神经网络 原理与实践》周浦城 李从利 王勇 韦哲 编著

出版社：北京：电子工业出版社，2020.10

ISBN: 978-7-121-39663-2

3.《Python神经网络 入门与实践》 王凯 编著

出版社：北京大学出版社

ISBN： 9787301316290
4. b站博主@霹雳吧啦Wz：https://www.bilibili.com/video/BV187411T7Ye/?spm_id_from=333.788&vd_source=647760d93691c99109dee33aad004b62