机器学习——ROC曲线、PR曲线

背景介绍

目录

背景介绍

ROC曲线

介绍

深入

ROC曲线的主要用途及其优点

补充

PR曲线

介绍

深入

使用场景

ROC曲线和PR曲线关系

具体实现

ROC曲线的实现

PR曲线的实现

实验总结

---

ROC曲线

介绍

ROC曲线（receiver operating characteristic）是一种对于灵敏度进行描述的功能图像，又称为感受性曲线（sensitivity curve。ROC曲线可以通过描述真阳性率（TPR）和假阳性率（FPR）来实现。由于是通过比较两个操作特征（TPR和FPR）作为标准，ROC曲线也叫做相关操作特征曲线。

ROC分析给选择最好的模型和在上下文或者类分布中抛弃一些较差的模型提供了工具。ROC曲线首先是由二战中的电子工程师和雷达工程师发明的，他们是用来检测战场中的敌军的，也就是信号检测理论。ROC分析现在已经在相关的领域得到了很好的发展，特别是在医学，无线电领域中，而且最近在机器学习和数据挖掘领域也得到了很好的发展。

深入

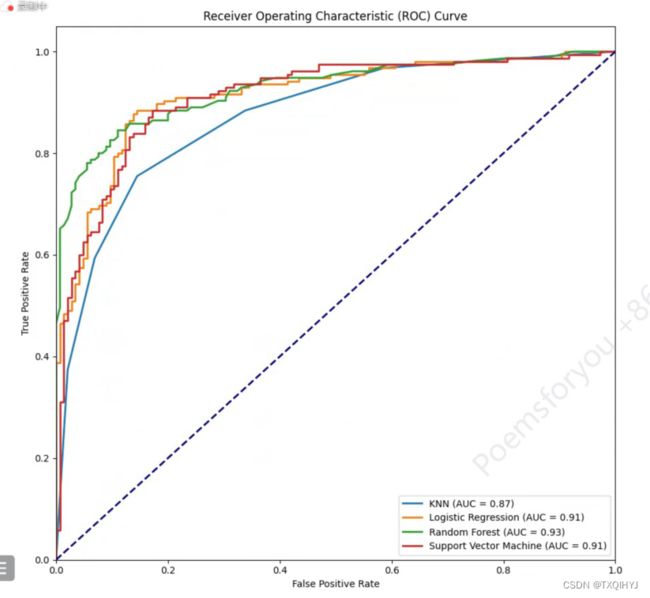
上图是一个以虚惊概率为横轴，击中概率为纵轴所组成的坐标图。如何判断哪个ROC曲线效果更好呢？我们常见：AUC(Area Under Curve)被定义为ROC曲线下的面积，取值范围一般在0.5和1之间(当AUC=0.5时，)。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。不难看出，ROC曲线越靠近坐标的左上角越好。

平面的横坐标是false positive rate(FPR)，纵坐标是true positive rate(TPR)。对某个分类器而言，我们可以根据其在测试样本上的表现得到一个TPR和FPR点对。这样，此分类器就可以映射成ROC平面上的一个点。调整这个分类器分类时候使用的阈值，我们就可以得到一个经过(0, 0)，(1, 1)的曲线，这就是此分类器的ROC曲线。

ROC曲线内概念的四种分类：

真正（True Positive , TP）被模型预测为正的正样本；

假负（False Negative , FN）被模型预测为负的正样本；

假正（False Positive , FP）被模型预测为正的负样本；

真负（True Negative , TN）被模型预测为负的负样本。

ROC曲线的主要用途及其优点

主要用途：

1.ROC曲线能很容易地查出任意界限值时的对性能的识别能力。
2.选择最佳的诊断界限值。ROC曲线越靠近左上角,试验的准确性就越高。最靠近左上角的ROC曲线的点是错误最少的最好阈值，其假阳性和假阴性的总数最少。
3.两种或两种以上不同诊断试验对算法性能的比较。在对同一种算法的两种或两种以上诊断方法进行比较时，可将各试验的ROC曲线绘制到同一坐标中，以直观地鉴别优劣，靠近左上角的ROC曲线所代表的受试者工作最准确。亦可通过分别计算各个试验的ROC曲线下的面积(AUC)进行比较，哪一种试验的 AUC最大，则哪一种试验的诊断价值最佳。

优点：

该方法简单、直观，通过图示可观察分析方法的准确性，并可用肉眼作出判断。ROC曲线将灵敏度与特异性以图示方法结合在一起，可准确反映某分析方法特异性和敏感性的关系，是试验准确性的综合代表。ROC曲线不固定分类界值，允许中间状态存在，利于使用者结合专业知识，权衡漏诊与误诊的影响，选择一更佳截断点作为诊断参考值。提供不同试验之间在共同标尺下的直观的比较，ROC曲线越凸越近左上角表明其诊断价值越大，利于不同指标间的比较。曲线下面积可评价诊断准确性

补充

真正类率(True Positive Rate, TPR)：TPR=TP/(TP+FN)

假正类率(False Positive Rate, FPR)：FPR=FP/(FP+TN)

PR曲线

介绍

P-R曲线刻画查准率和查全率之间的关系，查准率指的是在所有预测为正例的数据中，真正例所占的比例，查全率是指预测为真正例的数据占所有正例数据的比例。
即：精准率P=TP／(TP + FP)      召回率=TP／（TP+FN）
查准率和查全率是一对矛盾的度量，一般来说，查准率高时，查全率往往偏低，查全率高时，查准率往往偏低，例如，若希望将好瓜尽可能多选出来，则可通过增加选瓜的数量来实现，如果希望将所有的西瓜都选上，那么所有的好瓜必然都被选上了，但这样查准率就会较低；若希望选出的瓜中好瓜比例尽可能高，则可只挑选最有把握的瓜，但这样就难免会漏掉不少好瓜，使得查全率较低。

深入

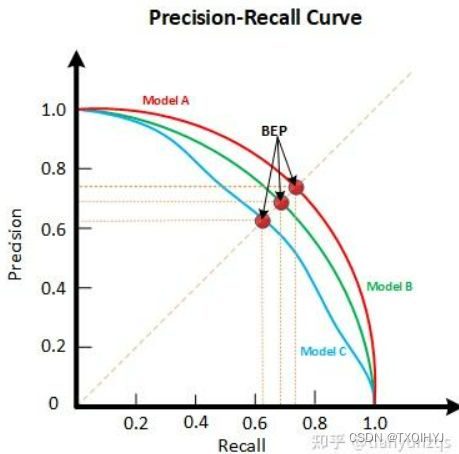
PR（Precision-Recall）曲线和ROC曲线类似，P代表的是precision（精准率），R代表的是recall（召回率），ROC曲线是FPR和TPR的点连成的线，PR曲线是准确率和召回率的点连成的线，如下图所示。

PR曲线的横坐标为召回率R，纵坐标为查准率P，绘制步骤如下： 1. 将预测结果按照预测为正类概率值排序； 2. 将概率阈值由1开始逐渐降低，按此顺序逐个把样本作为正例进行预测，每次可以计算出当前的P，R值； 3. 以P为纵坐标，R为横坐标绘制点，将所有点连成曲线后构成PR曲线。

precision（精准率）：precision = TP/(TP+FP)

recall（召回率）：recall = TP/(TP+FN)

使用场景

1.ROC曲线由于兼顾正例与负例，所以适用于评估分类器的整体性能，相比而言PR曲线完全聚焦于正例。
2.如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响，则ROC曲线比较适合，因为类别分布改变可能使得PR曲线发生变化时好时坏，这种时候难以进行模型比较；反之，如果想测试不同类别分布下对分类器的性能的影响，则PR曲线比较适合。
3.如果想要评估在相同的类别分布下正例的预测情况，则宜选PR曲线。
4.类别不平衡问题中，ROC曲线通常会给出一个乐观的效果估计，所以大部分时候还是PR曲线更好。
5.最后可以根据具体的应用，在曲线上找到最优的点，得到相对应的precision，recall，f1 score等指标，去调整模型的阈值，从而得到一个符合具体应用的模型。

ROC曲线和PR曲线关系

在ROC空间，ROC曲线越凸向左上方向效果越好。与ROC曲线左上凸不同的是，PR曲线是右上凸效果越好。

ROC和PR曲线都被用于评估机器学习算法对一个给定数据集的分类性能，每个数据集都包含固定数目的正样本和负样本。而ROC曲线和PR曲线之间有着很深的关系。

  定理1：对于一个给定的包含正负样本的数据集，ROC空间和PR空间存在一一对应的关系，也就是说，如果recall不等于0，二者包含完全一致的混淆矩阵。我们可以将ROC曲线转化为PR曲线，反之亦然。

定理2：对于一个给定数目的正负样本数据集，一条曲线在ROC空间中比另一条曲线有优势，当且仅当第一条曲线在PR空间中也比第二条曲线有优势。（这里的“一条曲线比其他曲线有优势”是指其他曲线的所有部分与这条曲线重合或在这条曲线之下。）

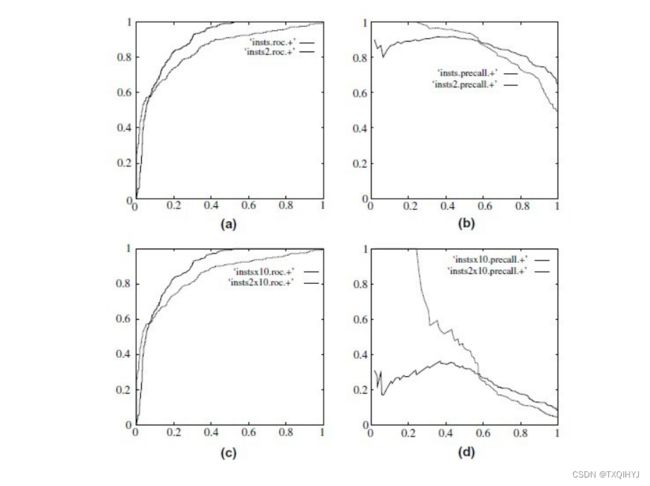
当正负样本差距不大的情况下，ROC和PR的趋势是差不多的，但是当负样本很多的时候，两者就截然不同了，ROC效果依然看似很好，但是PR上反映效果一般。解释起来也简单，假设就1个正例，100个负例，那么基本上TPR可能一直维持在100左右，然后突然降到0.如图，(a)(b)分别为正负样本1:1时的ROC曲线和PR曲线，二者比较接近。而(c)(d)的正负样本比例为1:1，这时ROC曲线效果依然很好，但是PR曲线则表现的比较差。这就说明PR曲线在正负样本比例悬殊较大时更能反映分类的性能。

具体实现

ROC曲线的实现

具体代码：

from sklearn.metrics import roc_curve, auc
import numpy as np
##y_test相当于真实值，注意，roc曲线仅适用于二分类问题，多分类问题应先转化为二分类
y_test = np.array([1,1,0,1,1,1,0,0,1,0,1,0,1,0,0,0,1,0,1,0,1,0,0,1,1,1,1,0,0,1,0,0,1,0])
y_score = np.array([0.9,0.8,0.7,0.6,0.55,0.54,0.53,0.52,0.51,0.505,0.4,0.39,0.38,0.37,0.36,0.35,0.34,0.33,0.3,0.1,0.5,0.3,0.34,0.9,0.55,0.54,0.53,0.52,0.51,0.4,0.39,0.38,0.37,0.36])
##
fpr,tpr,thre = roc_curve(y_test,y_score)
##计算auc的值，就是roc曲线下的面积
auc = auc(fpr,tpr)
##画图
plt.plot(fpr,tpr,color = 'darkred',label = 'roc area:(%0.2f)'%auc)
plt.plot([0,1],[0,1],linestyle = '--')
plt.xlim([0,1])
plt.ylim([0,1])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc = 'lower right')

自定义数据：

运行结果：

补充

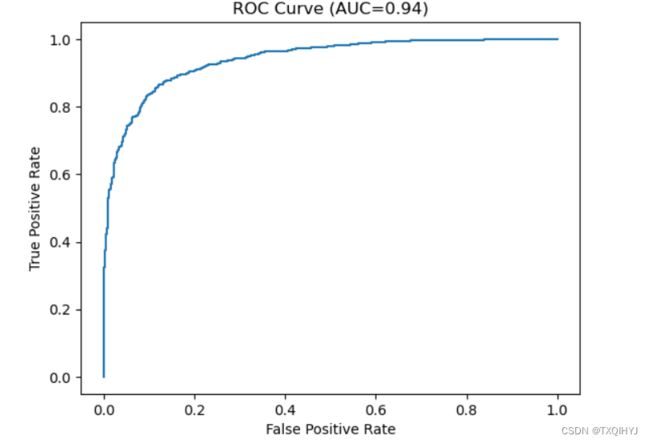
由于之前是由自己输入的数据绘制的ROC曲线，所以曲线不是那么平滑，一下我采用随机生成二分类数据集并绘制ROC曲线，我随机生成包含1000个样本的数据集，这样绘制出来的ROC曲线就会更加平滑了，如下：

具体代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score

# 随机生成两个类别的样本数据
np.random.seed(42)

# 正类样本（标签为1）
num_samples_positive = 1000
positive_mean = [1, 1]  # 正类样本的均值
positive_cov = [[2, 0], [0, 2]]  # 正类样本的协方差矩阵
positive_samples = np.random.multivariate_normal(positive_mean, positive_cov, num_samples_positive)

# 负类样本（标签为0）
num_samples_negative = 1000
negative_mean = [-1, -1]  # 负类样本的均值
negative_cov = [[1, 0.5], [0.5, 1]]  # 负类样本的协方差矩阵
negative_samples = np.random.multivariate_normal(negative_mean, negative_cov, num_samples_negative)

# 合并正类和负类样本
X = np.concatenate((positive_samples, negative_samples), axis=0)
y = np.concatenate((np.ones(num_samples_positive), np.zeros(num_samples_negative)))

# 使用逻辑回归模型对样本进行训练
model = LogisticRegression(random_state=42)
model.fit(X, y)

# 预测概率值
y_pred_prob = model.predict_proba(X)[:, 1]

# 计算FPR、TPR和AUC评分，并绘制ROC曲线
fpr, tpr, thresholds = roc_curve(y, y_pred_prob)
roc_auc = roc_auc_score(y, y_pred_prob)

plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title(f'ROC Curve (AUC={roc_auc:.2f})')
plt.show()

运行结果：

不难看出，相较于之前自己手动设置的数据（数目太少，所以ROC曲线不平滑），这次的ROC曲线显得平滑许多了。

PR曲线的实现

具体代码：

from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt

# 自定义数据
y_test = np.array([1,1,0,1,1,1,0,0,1,0,1,0,1,0,0,0,1,0,1,0])
y_score = np.array([0.9,0.8,0.7,0.6,0.55,0.54,0.53,0.52,0.51,0.505,0.4,0.39,0.38,0.37,0.36,0.35,0.34,0.33,0.3,0.1])

# 计算precision和recall
precision, recall, thresholds = precision_recall_curve(y_test, y_score)

# 绘制PR曲线
plt.plot(recall, precision, color='darkblue', label='PR Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc='lower left')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.show()

自定义数据：

运行结果：

实验总结

ROC曲线和PR曲线都是衡量分类器性能的重要工具。其中，ROC曲线可以表示分类器在正负样本比例不平衡的情况下分类性能，而PR曲线则更加关注分类器能够正确检测出正例的性能。

具体来说，ROC曲线可以帮助我们判断分类器效果的好坏，ROC曲线越接近左上角，说明分类器的效果越好，AUC值也越高。而PR曲线则主要用于评估正例的检测能力，当正例数量比较少时，PR曲线的效果优于ROC曲线。

在实际应用中，我们需要根据不同的任务需求来选择采用哪种曲线进行性能评估。如果关注的是分类器对不同阈值下的性能表现，比如二分类或多分类问题中判定阈值的设置，采用ROC曲线更为恰当；反之，如果关注的是分类器对正例的检测能力，比如医学诊断、垃圾邮件过滤、异常检测等任务，采用PR曲线更为合适。

总之，ROV曲线和PR曲线都是非常有用的工具，通过它们可以直观地看出我们的分类器在不同任务中的性能表现。在实际应用中需要综合考虑任务需求，结合实际情况选择合适的性能评估方法。

资料参考： ROC曲线和PR曲线  

                  分类评价指标：ROC曲线和PR曲线详解

                 ROC曲线和PR(Precision-Recall)曲线的联系