逻辑回归简单案例分析--鸢尾花数据集
文章目录
-
- 1. IRIS数据集介绍
- 2. 具体步骤
-
- 2.1 手动将数据转化为numpy矩阵
-
- 2.1.1 从csv文件数据构建Numpy数据
- 2.1.2 模型的搭建与训练
- 2.1.3 分类器评估
- 2.1.4 分类器的分类报告总结
- 2.1.5 用交叉验证(Cross Validation)来验证分类器性能
- 2.1.6 完整代码:
- 2.2 使用sklearn内置的iris数据集(多分类)
-
- 2.2.1 导入数据集
- 2.2.2 划分训练集和测试集
- 2.2.3 定义逻辑回归模型并训练
- 2.2.5 用训练好的模型在训练集和测试集上做预测
- 2.2.6 对预测结果进行可视化
1. IRIS数据集介绍
Iris也称鸢尾花卉数据集,是常用的分类实验数据集,由R.A. Fisher于1936年收集整理的。其中包含3种植物种类,分别是山鸢尾(setosa)变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica),每类50个样本,共150个样本。
该数据集包含4个特征变量,1个类别变量。iris每个样本都包含了4个特征:花萼长度,花萼宽度,花瓣长度,花瓣宽度,以及1个类别变量(label)。我们需要建立一个分类器,分类器可以通过这4个特征来预测鸢尾花卉种类是属于山鸢尾,变色鸢尾还是维吉尼亚鸢尾。其中有一个类别是线性可分的,其余两个类别线性不可分,这在最后的分类结果绘制图中可观察到。
| 变量名 | 变量解释 | 数据类型 |
|---|---|---|
| sepal_length | 花萼长度(单位cm) | numeric |
| sepal_width | 花萼宽度(单位cm) | numeric |
| petal_length | 花瓣长度(单位cm) | numeric |
| petal_width | 花瓣长度(单位cm) | categorical |
2. 具体步骤
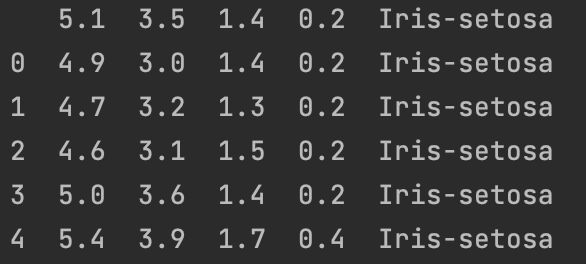
Step1:数据集预览
df=pd.read_csv('./data/iris.data.csv',header=0)
print(df.head())
2.1 手动将数据转化为numpy矩阵
2.1.1 从csv文件数据构建Numpy数据
Step 1:构造映射函数iris_type。因为实际数据中,label并不都是便于学习分类的数字型,而是string类型。
Step 2:对于文本类的label, 将label列的所有内容都转变成映射函数的输出,存成新的dataframe
Step 3:将Step2的结果转换成numpy矩阵
Step 4:划分训练集与测试集
def iris_type(s):
class_label={'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return class_label[s]
df=pd.read_csv('./data/iris.data.csv',header=0)
#2.将第4列内容映射至iris_type函数定义的内容
df['Species']=df['Species'].apply(iris_type)
print(df.head())
#3.将df解析到numpy_arrat
data=np.array(df)
# print(data[:2])
#4.将原始数据集分为测试集合和验证集合
# 用np.split按列(axis=1)进行分割
# (4,):分割位置,前4列作为x的数据,第4列之后都是y的数据
x,y=np.split(data,(4,),axis=1)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.7,random_state=0)
2.1.2 模型的搭建与训练
-
Pipeline(steps)
利用sklearn提供的管道机制
Pipeline
来实现对全部步骤的流式化封装与管理。
- 第一个环节:可以先进行 数据标准化 StandardScaler()
- 中间环节:可以加上 PCA降维处理 取2个重要特征
- 最终环节:逻辑回归分类器
pip_LR=Pipeline([('sc',StandardScaler()),
('pca',PCA(n_components=2)),
('clf_lr',LogisticRegression(random_state=1))
])
#开始训练
pip_LR.fit(x_train,y_train.ravel())
#显示当前管道的配置和参数设置,它并没有直接运行或产生实际的影响,只展示了机器学习管道的配置
Pipeline(memory=None,
steps=[('sc', StandardScaler(copy=True, with_mean=True, with_std=True)), ('pca', PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)), ('clf_lr', LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=1, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False))])
2.1.3 分类器评估
print("训练准确率:%0.2f"%pip_LR.score(x_train,y_train))
print("测试准确率:%0.2f"%pip_LR.score(x_test,y_test))
y_hat=pip_LR.predict(x_test)
accuracy=metrics.accuracy_score(y_test,y_hat)
print("逻辑回归分类器的准确率:%0.2f" % accuracy)
2.1.4 分类器的分类报告总结
- 精确度(Precision):指的是在所有模型预测为某一类别的样本中,真正属于该类别的比例。计算方式为该类别的 True Positives / (True Positives + False Positives)。
- 召回率(Recall):指的是在所有实际属于某一类别的样本中,被模型正确预测为该类别的比例。计算方式为该类别的 True Positives / (True Positives + False Negatives)
- F1 Score:是精确度和召回率的调和平均数,综合考虑了两者的性能。计算方式为 2 ∗ P r e c s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l 2*\frac{Precsion*Recall}{Precision+Recall} 2∗Precision+RecallPrecsion∗Recall
- support:指的是属于该类别的样本数。
- accuracy(准确度):指的是模型在所有类别上正确预测的比例。计算方式为 Sum of True PositivesTotal SamplesTotal SamplesSum of True Positives。
- macro avg(宏平均):对所有类别的指标取平均,不考虑类别样本数量的差异。
- weighted avg(加权平均):对所有类别的指标取加权平均,考虑类别样本数量的差异。
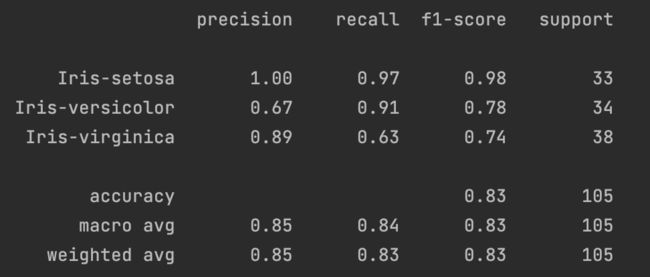
#描述分类器的精确度,召回率,F1Score
target_names=['Iris-setosa','Iris-versicolor','Iris-virginica']
print(metrics.classification_report(y_test,y_hat,target_names=target_names))
2.1.5 用交叉验证(Cross Validation)来验证分类器性能
交叉验证常用于防止模型过于复杂而造成过拟合,同时也称为循环估计。基本思想是将原始数据分成K组(一般是平均分组),每个子集数据分别做一次验证集或测试集,其余的K-1个子集作为训练集。这样就会得到K个模型,取这K个模型的分类准确率的平均数作为分类器的性能指标更具说服力。
比如说在这里我们使用的是5折交叉验证(5-fold cross validation),即数据集被分成了5份,轮流将其中4份作为训练数据集,剩余1份作为测试集,进行试验。每次试验都会得出相应的正确率,将5次试验得出的相应正确率的平均值作为分类器的准确率的估计。同样的,K也可以取10,20等。
iris_data=x
iris_target=y
scores=cross_val_score(pip_LR,iris_data,iris_target.ravel(),cv=5,scoring='f1_macro')
print("5折交叉验证:\n逻辑回归分类器的准确率:%.2f 误差范围:(+/- %.2f)"%(scores.mean(), scores.std()*2))
X_trainval, X_test, y_trainval, y_test = train_test_split(
iris_data, iris_target, random_state=0)
X_train, X_val, y_train, y_val = train_test_split(
X_trainval, y_trainval, random_state=1)
print("训练集大小:{} 验证集大小:{} 测试集大小:{}".format(
X_train.shape[0],
X_val.shape[0],
X_test.shape[0]))
2.1.6 完整代码:
#将原始数据文件转为机器学习可用的numpy数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import plotly.express as px
import chart_studio.grid_objs as go
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
def iris_type(s):
class_label={'Iris-setosa':0,'Iris-versicolor':1,'Iris-virginica':2}
return class_label[s]
df=pd.read_csv('./data/iris.data.csv',header=0)
#2.将第4列内容映射至iris_type函数定义的内容
df['Species']=df['Species'].apply(iris_type)
print(df.head())
#3.将df解析到numpy_arrat
data=np.array(df)
# print(data[:2])
#4.将原始数据集分为测试集合和验证集合
# 用np.split按列(axis=1)进行分割
# (4,):分割位置,前4列作为x的数据,第4列之后都是y的数据
x,y=np.split(data,(4,),axis=1)
# X = x[:,0:2] # 取前两列特征
# 用train_test_split将数据按照7:3的比例分割训练集与测试集,
# 随机种子设为1(每次得到一样的随机数),设为0或不设(每次随机数都不同)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.7,random_state=0)
pip_LR=Pipeline([('sc',StandardScaler()),
('pca',PCA(n_components=2)),
('clf_lr',LogisticRegression(random_state=1))
])
#开始训练
pip_LR.fit(x_train,y_train.ravel())
#显示当前管道的配置和参数设置,它并没有直接运行或产生实际的影响,只展示了机器学习管道的配置
Pipeline(memory=None,
steps=[('sc', StandardScaler(copy=True, with_mean=True, with_std=True)), ('pca', PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)), ('clf_lr', LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=1, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False))])
print("训练准确率:%0.2f"%pip_LR.score(x_train,y_train))
print("测试准确率:%0.2f"%pip_LR.score(x_test,y_test))
y_hat=pip_LR.predict(x_test)
accuracy=metrics.accuracy_score(y_test,y_hat)
print("逻辑回归分类器的准确率:%0.2f" % accuracy)
#描述分类器的精确度,召回率,F1Score
target_names=['Iris-setosa','Iris-versicolor','Iris-virginica']
print(metrics.classification_report(y_test,y_hat,target_names=target_names))
#交叉验证(Cross Validation)来验证分类器的性能
iris_data=x
iris_target=y
scores=cross_val_score(pip_LR,iris_data,iris_target.ravel(),cv=5,scoring='f1_macro')
print("5折交叉验证:\n逻辑回归分类器的准确率:%.2f 误差范围:(+/- %.2f)"%(scores.mean(), scores.std()*2))
X_trainval, X_test, y_trainval, y_test = train_test_split(
iris_data, iris_target, random_state=0)
X_train, X_val, y_train, y_val = train_test_split(
X_trainval, y_trainval, random_state=1)
print("训练集大小:{} 验证集大小:{} 测试集大小:{}".format(
X_train.shape[0],
X_val.shape[0],
X_test.shape[0]))
网格搜索验证见:用逻辑回归实现鸢尾花数据集分类(2) - Heywhale.com
2.2 使用sklearn内置的iris数据集(多分类)
2.2.1 导入数据集
#导入内置数据集,已经处理空置,无需进行预处理
iris = load_iris()
print('数据集的前5个样例', iris.data[0:5])
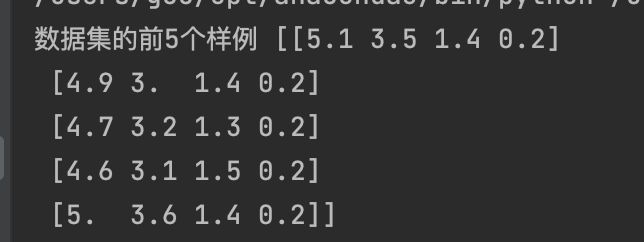
2.2.2 划分训练集和测试集
y = iris.target
X = iris.data
X_train, X_test, Y_train, Y_test = train_test_split(X, y, train_size=0.8, random_state=2020)
2.2.3 定义逻辑回归模型并训练
logistic = LogisticRegression(random_state=0,solver='lbfgs')
logistic.fit(X_train, Y_train)
print('the weight of Logistic Regression:\n',logistic.coef_)
print('the intercept(w0) of Logistic Regression:\n',logistic.intercept_)
y_train_predict=logistic.predict(X_train)
y_test_predict = logistic.predict(X_test)
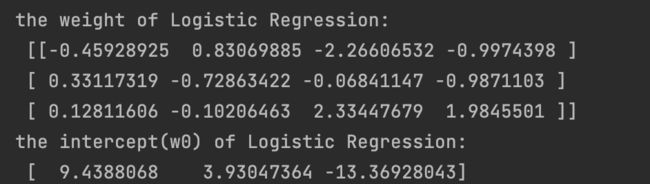
可以看到此处打印出了三组参数,这是因为这里我们是三分类问题。
2.2.5 用训练好的模型在训练集和测试集上做预测
#由于逻辑回归模型是概率预测模型,所有我们可以利用 predict_proba 函数预测其概率
train_predict_proba = logistic.predict_proba(X_train)
test_predict_proba = logistic.predict_proba(X_test)
print('The test predict Probability of each class:\n',test_predict_proba)
# 利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(Y_train,y_train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(Y_test,y_test_predict))
confusion_matrix_result = metrics.confusion_matrix(y_test_predict,Y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
2.2.6 对预测结果进行可视化
confusion_matrix_result = metrics.confusion_matrix(y_test_predict,Y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
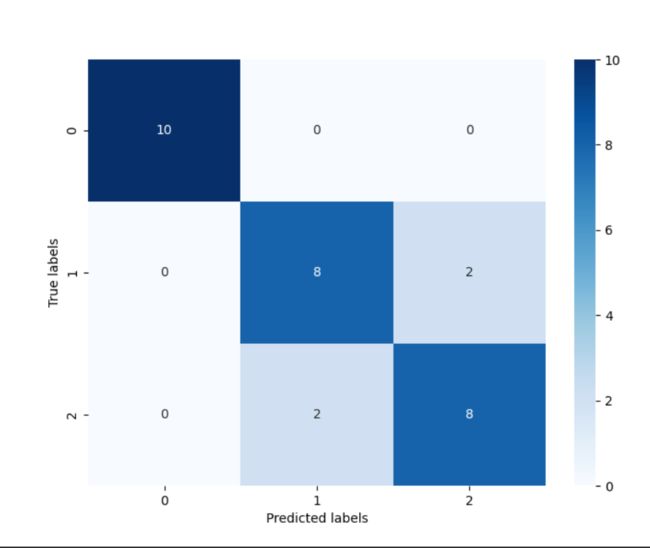
通过结果我们可以发现,其在三分类的结果其在测试集上的准确度为: 86.67% ,这是由于’versicolor’(1)和 ‘virginica’(2)这两个类别的特征,我们从可视化的时候也可以发现,其特征的边界具有一定的模糊性(边界类别混杂,没有明显区分边界),所有在这两类的预测上出现了一定的错误。
从混淆矩阵中可以看出:标签值y=0的10个样本都被正确分类;标签值y=1的10个样本中,有8个被正确分类,其中有两个被误分类为y=2;标签值y=2的10个样本中,有8个被正确分类,其中有两个被误分类为y=1。