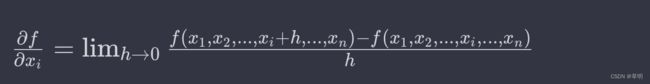偏导函数公式以及使用 python 计算

偏导函数

偏导函数是多元函数对其中一个变量的偏导数。对于一个多元函数，其输入变量有两个或更多，而偏导函数则表示对其中一个变量的偏导数，将其他变量视为常数。

设有一个具有 n 个自变量的函数 f(,,...,)，则对于其中的某一个自变量 ​，其偏导函数记作 ​，表示在其他变量保持不变的条件下，函数对  的偏导数。

数学上，偏导数的定义如下：

其中，h 是一个趋近于零的数。

在计算上，可以通过类似于一元函数求导的方法，将其他自变量视为常数，对其中一个变量求导来得到偏导数。例如，对于函数 f(x,y)，分别对 x 和 y 求偏导数，得到：

和

偏导数在数学、物理、工程等领域中都有广泛的应用，特别是在描述多变量系统的变化率、梯度、最小值和最大值等方面。

使用 Python 中计算偏导数，

可以使用一些数学库，如SymPy或NumPy。

SymPy

以下是使用SymPy进行偏导数计算的简单示例：

首先，确保已经安装了SymPy：

pip install sympy

然后，可以使用以下代码计算一个简单函数的偏导数：

from sympy import symbols, diff

# 定义变量和函数
x, y = symbols('x y')
f = x**2 + y**3

# 计算偏导数
df_dx = diff(f, x)
df_dy = diff(f, y)

# 打印结果
print("偏导数 df/dx:", df_dx)
print("偏导数 df/dy:", df_dy)

在这个例子中，我们定义了一个简单的函数 f = x**2 + y**3，然后使用SymPy的 diff 函数计算了关于变量 x 和 y 的偏导数。可以将上述代码中的函数替换为想要计算偏导数的任何函数。

请注意，SymPy返回的结果是表达式，如果需要数值结果，可以将具体的值代入表达式中。例如：

# 替换变量并计算具体值
x_value = 2
y_value = 3

result_dx = df_dx.subs({x: x_value, y: y_value})
result_dy = df_dy.subs({x: x_value, y: y_value})

print(f"在 x={x_value}, y={y_value} 处的偏导数 df/dx 的值为:", result_dx)
print(f"在 x={x_value}, y={y_value} 处的偏导数 df/dy 的值为:", result_dy)
np

这将计算在 x=2, y=3 处的偏导数的具体值。

NumPy

NumPy是一个用于科学计算的强大库，可以用于计算数值函数的偏导数。下面是一个使用NumPy计算偏导数的简单示例：

首先，确保已经安装了NumPy：

pip install numpy

然后，可以使用以下代码计算一个简单函数的偏导数：

import numpy as np

# 定义函数
def f(x, y):
    return x**2 + y**3

# 定义计算偏导数的函数
def partial_derivative(func, var=0, point=[]):
    args = point[:]
    def wraps(x):
        args[var] = x
        return func(*args)
    return np.vectorize(wraps)

# 定义变量和计算点
x_value = 2
y_value = 3

# 计算偏导数
df_dx = partial_derivative(f, var=0, point=[x_value, y_value])
df_dy = partial_derivative(f, var=1, point=[x_value, y_value])

# 打印结果
print(f"在 x={x_value}, y={y_value} 处的偏导数 df/dx 的值为:", df_dx(x_value))
print(f"在 x={x_value}, y={y_value} 处的偏导数 df/dy 的值为:", df_dy(y_value))

在这个例子中，我们定义了一个简单的函数 f = x**2 + y**3，然后使用 partial_derivative 函数计算了关于变量 x 和 y 的偏导数。这里使用了NumPy的vectorize 函数，允许我们向量化计算，以便一次性传入多个点进行计算。

可以将上述代码中的函数替换为想要计算偏导数的任何函数。这种方法适用于数值计算，但在一些特殊情况下，对于符号计算，SymPy可能更为适合。