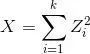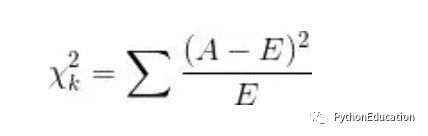卡方分箱(chi-square)

统计学，风控建模经常遇到卡方分箱算法ChiMerge。卡方分箱在金融信贷风控领域是逻辑回归评分卡的核心，让分箱具有统计学意义（单调性）。卡方分箱在生物医药领域可以比较两种药物或两组病人是否具有显著区别。但很多建模人员搞不清楚卡方分箱原理。先给大家介绍一下经常被提到的卡方分布和卡方检验是什么。欢迎各位同学学习更多相关知识python金融风控评分卡模型和数据分析：https://edu.csdn.net/combo/detail/1927

一、卡方分布

卡方分布(chi-square distribution, χ2-distribution)是概率统计里常用的一种概率分布，也是统计推断里应用最广泛的概率分布之一，在假设检验与置信区间的计算中经常能见到卡方分布的身影。

卡方分布的定义如下：

若k个独立的随机变量Z1, Z2,..., Zk 满足标准正态分布 N(0,1) , 则这k个随机变量的平方和：

为服从自由度为k的卡方分布，记作：

或者记作

二、卡方检验

χ2检验是以χ2分布为基础的一种假设检验方法，主要用于分类变量之间的独立性检验。

其基本思想是根据样本数据推断总体的分布与期望分布是否有显著性差异，或者推断两个分类变量是否相关或者独立。

一般可以设原假设为 ：观察频数与期望频数没有差异，或者两个变量相互独立不相关。

实际应用中，我们先假设原假设成立，计算出卡方的值，卡方表示观察值与理论值间的偏离程度。

卡方值的计算公式为：

其中A为实际频数，E为期望频数。卡方值用于衡量实际值与理论值的差异程度，这也是卡方检验的核心思想。

卡方值包含了以下两个信息：

1.实际值与理论值偏差的绝对大小。2.差异程度与理论值的相对大小。

上述计算的卡方值服从卡方分布。根据卡方分布，卡方统计量以及自由度，可以确定在原假设成立的情况下获得当前统计量以及更极端情况的概率p。如果p很小，说明观察值与理论值的偏离程度大，应该拒绝原假设。否则不能拒绝原假设。

三、卡方检验实例

某医院对某种病症的患者使用了A，B两种不同的疗法，结果如表1，问两种疗法有无差别？

表1 两种疗法治疗卵巢癌的疗效比较

可以计算出各格内的期望频数。

第1行1列：43×53/87=26.2

第1行2列：43×34/87=16.8

第2行1列：44×53/87=26.8

第2行2列：4×34/87=17.2

先建立原假设：A、B两种疗法没有区别。根据卡方值的计算公式，计算：

算得卡方值=10.01。

得到卡方值以后，接下来需要查询卡方分布表来判断p值，从而做出接受或拒绝原假设的决定。

首先我们明确自由度的概念：自由度k=(行数-1)*(列数-1)。这里k=1.然后看卡方分布的临界概率表，我们可以用如下代码生成：

1. #python金融风控评分卡模型和数据分析：https://edu.csdn.net/combo/detail/1927

2. #讲师csdn学院教学主页：https://edu.csdn.net/lecturer/5602

4. from scipy.stats import chi2

6. # chi square distribution

7. percents = [ 0.95, 0.90, 0.5,0.1, 0.05, 0.025, 0.01, 0.005]

8. df =pd.DataFrame(np.array([chi2.isf(percents, df=i) for i in range(1, 30)]))

11. pd.set_option('precision', 3)

查表自由度为1,p=0.05的卡方值为3.841，而此例卡方值10.01>3.841，因此 p < 0.05，说明原假设在0.05的显著性水平下是可以拒绝的。也就是说，原假设不成立。

四、ChiMerge分箱算法

ChiMerge卡方分箱算法由Kerber于1992提出。

它主要包括两个阶段：初始化阶段和自底向上的合并阶段。

1.初始化阶段：

首先按照属性值的大小进行排序（对于非连续特征，需要先做数值转换，比如转为坏人率，然后排序），然后每个属性值单独作为一组。

2.合并阶段：

（1）对每一对相邻的组，计算卡方值。

（2）根据计算的卡方值，对其中最小的一对邻组合并为一组。

（3）不断重复（1），（2）直到计算出的卡方值都不低于事先设定的阈值，或者分组数达到一定的条件（如最小分组数5，最大分组数8）。

值得注意的是，小编之前发现有的实现方法在合并阶段，计算的并非相邻组的卡方值（只考虑在此两组内的样本，并计算期望频数），因为他们用整体样本来计算此相邻两组的期望频数。

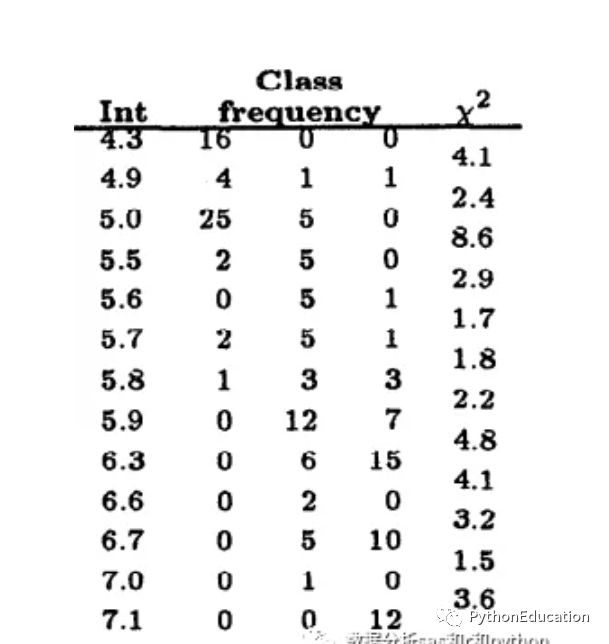
下图是著名的鸢尾花数据集sepal-length属性值的分组及相邻组的卡方值。最左侧是属性值，中间3列是class的频数，最右是卡方值。这个分箱是以卡方阈值1.4的结果。可以看出，最小的组为[6.7，7.0），它的卡方值是1.5。

如果进一步提高阈值，如设置为4.6，那么以上分箱还将继续合并，最终的分箱如下图：

卡方分箱除了用阈值来做约束条件，还可以进一步的加入分箱数约束，以及最小箱占比，坏人率约束等。

卡方分箱之python代码实

在上篇文章中，介绍了卡方分箱的基本思想和方法，都是概念性的东西，也没有给出具体的代码实现。这篇文章就来介绍下小编写的ChiMerge算法的实现。

卡方值计算

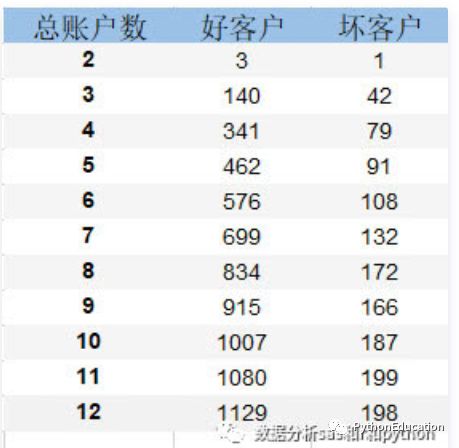
计算卡方值的函数需要输入numpy格式的频数表。对于pandas数据集，只需使用pd.crosstab计算即可，例如变量“总账户数” 与 目标变量 “是否坏客户” 的频数表，如下图：

每一行代表一个区间（组）的频数，如上图中第一行表示 总账户数在[2,3) 这个组内对应的好客户3个， 坏客户1个。

将频数表转成numpy数组，然后调用函数计算卡方值，计算逻辑如下：

1） 计算第 i 行的总数。

2） 计算第 j 列的总数。

3） 计算总频数 N。

4） 计算 第 i,j 格的期望频数。

5）求的每个格中的卡方:

6） 由于期望频数 Ei,j有可能是0，此时上一步计算出来的结果无意义，需要清除，不计入最终结果。

7） 把所有格的卡方相加得到卡方值。

代码如下

'author:xiaodongxu&monica'

ChiMerge分箱算法

卡方分箱函数可以根据最大分组数目和卡方阈值来控制最终的分箱数。

如果调用时既没有设置最大分组数，也没有指定阈值，那么函数会自动使用95%的置信度设置阈值。

分箱逻辑是：

1）初始时，所有变量值都自成一组，统计频数。

2）然后按照各组起始值从小到大，依次扫描，取出两组拼成计算卡方值。

如果当前计算出的卡方值小于已观察到的最小卡方值，则标记当前坐标，并更新已观察最小卡方值为当前值。

3）扫描一遍后，如果当前分组数大于最大分组数，或者最小卡方值小于阈值，就将最小卡方值对应的两组频数合并，区间也合并。并回第2步执行。否则，停止合并。输出当前各组的区间切分点。

代码如下

'author:xiaodongxu&monica'

变量值转分组

卡方分箱完成后，得到了各个分组的区间起始值。对于任给的一个变量值x，可以使用如下的函数获得分组值。

代码如下

'author:xiaodongxu&monica'

需要注意的是，如果需要转换的值x不在分箱区间之内，很有可能是异常值，不应该期望上面的函数来处理这种情况，而应采用专门的异常值处理程序。

评分卡建模中的使用实例

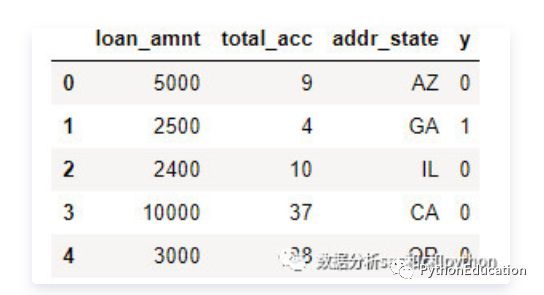
下面介绍一下评分卡建模中的卡方分箱的使用。先来看看数据集。

除了y变量外，还有3个变量：贷款额度（loan_amnt，数值型），总账户数（total_acc，数值型），地址州（addr_state，类别型）。

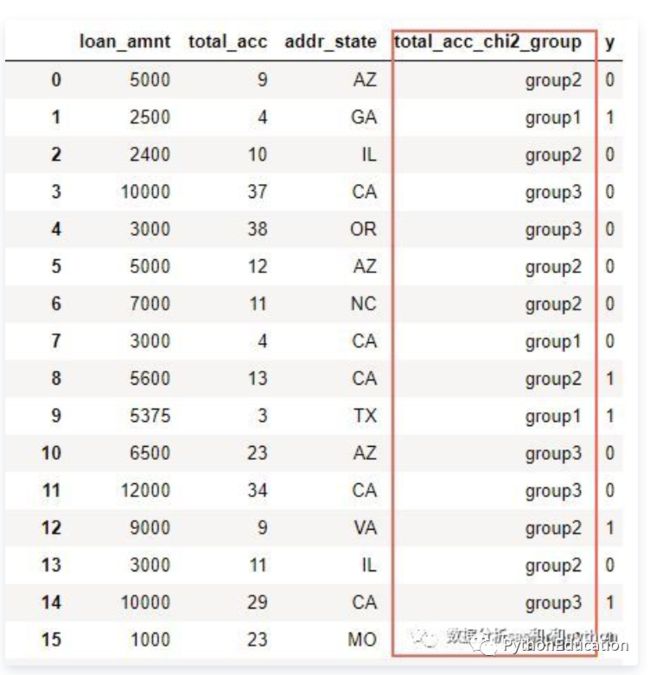
对总账户数total_acc进行分箱:

根据分箱结果进行转换，衍生新的分组变量：

现在已经将 total_acc衍生成为新的类别型变量 total_acc_chi2_group ，接下来可以用WOE编码继续加工，然后进入模型啦。

python卡方分箱实战脚本

 对数据框中的某个变量进行有监督的分箱操作

#python金融风控评分卡模型和数据分析：https://edu.csdn.net/combo/detail/1927

#讲师csdn学院教学主页：https://edu.csdn.net/lecturer/5602


data = pd.read_csv('sample_data.csv', sep="\t", na_values=['', '?'])



# 定义一个卡方分箱（可设置参数置信度水平与箱的个数）停止条件为大于置信水平且小于bin的数目

def ChiMerge(df, variable, flag, confidenceVal=3.841, bin=10, sample = None):

运行前需要 import pandas as pd 和 import numpy as np

df:传入一个数据框仅包含一个需要卡方分箱的变量与正负样本标识（正样本为1，负样本为0）

variable:需要卡方分箱的变量名称（字符串）

confidenceVal：置信度水平（默认是不进行抽样95%）

sample: 为抽样的数目（默认是不进行抽样），因为如果观测值过多运行会较慢



df = df.sample(n=sample)




total_num = df.groupby([variable])[flag].count() # 统计需分箱变量每个值数目

total_num = pd.DataFrame({'total_num': total_num}) # 创建一个数据框保存之前的结果

positive_class = df.groupby([variable])[flag].sum() # 统计需分箱变量每个值正样本数

positive_class = pd.DataFrame({'positive_class': positive_class}) # 创建一个数据框保存之前的结果

regroup = pd.merge(total_num, positive_class, left_index=True, right_index=True,

how='inner') # 组合total_num与positive_class

regroup.reset_index(inplace=True)

regroup['negative_class'] = regroup['total_num'] - regroup['positive_class'] # 统计需分箱变量每个值负样本数

regroup = regroup.drop('total_num', axis=1)

np_regroup = np.array(regroup) # 把数据框转化为numpy（提高运行效率）

print('已完成数据读入,正在计算数据初处理')

#处理连续没有正样本或负样本的区间，并进行区间的合并（以免卡方值计算报错）

while (i <= np_regroup.shape[0] - 2):

if ((np_regroup[i, 1] == 0 and np_regroup[i + 1, 1] == 0) or ( np_regroup[i, 2] == 0 and np_regroup[i + 1, 2] == 0)):

np_regroup[i, 1] = np_regroup[i, 1] + np_regroup[i + 1, 1] # 正样本

np_regroup[i, 2] = np_regroup[i, 2] + np_regroup[i + 1, 2] # 负样本

np_regroup[i, 0] = np_regroup[i + 1, 0]

np_regroup = np.delete(np_regroup, i + 1, 0)




chi_table = np.array([]) # 创建一个数组保存相邻两个区间的卡方值

for i in np.arange(np_regroup.shape[0] - 1):

chi = (np_regroup[i, 1] * np_regroup[i + 1, 2] - np_regroup[i, 2] * np_regroup[i + 1, 1]) ** 2 \

* (np_regroup[i, 1] + np_regroup[i, 2] + np_regroup[i + 1, 1] + np_regroup[i + 1, 2]) / \

((np_regroup[i, 1] + np_regroup[i, 2]) * (np_regroup[i + 1, 1] + np_regroup[i + 1, 2]) * (

np_regroup[i, 1] + np_regroup[i + 1, 1]) * (np_regroup[i, 2] + np_regroup[i + 1, 2]))

chi_table = np.append(chi_table, chi)

print('已完成数据初处理，正在进行卡方分箱核心操作')



if (len(chi_table) <= (bin - 1) and min(chi_table) >= confidenceVal):

chi_min_index = np.argwhere(chi_table == min(chi_table))[0] # 找出卡方值最小的位置索引

np_regroup[chi_min_index, 1] = np_regroup[chi_min_index, 1] + np_regroup[chi_min_index + 1, 1]

np_regroup[chi_min_index, 2] = np_regroup[chi_min_index, 2] + np_regroup[chi_min_index + 1, 2]

np_regroup[chi_min_index, 0] = np_regroup[chi_min_index + 1, 0]

np_regroup = np.delete(np_regroup, chi_min_index + 1, 0)

if (chi_min_index == np_regroup.shape[0] - 1): # 最小值试最后两个区间的时候

# 计算合并后当前区间与前一个区间的卡方值并替换

chi_table[chi_min_index - 1] = (np_regroup[chi_min_index - 1, 1] * np_regroup[chi_min_index, 2] - np_regroup[chi_min_index - 1, 2] * np_regroup[chi_min_index, 1]) ** 2 \

* (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) / \

((np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2]) * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) * (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index, 1]) * (np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 2]))

chi_table = np.delete(chi_table, chi_min_index, axis=0)


# 计算合并后当前区间与前一个区间的卡方值并替换

chi_table[chi_min_index - 1] = (np_regroup[chi_min_index - 1, 1] * np_regroup[chi_min_index, 2] - np_regroup[chi_min_index - 1, 2] * np_regroup[chi_min_index, 1]) ** 2 \

* (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) / \

((np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2]) * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) * (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index, 1]) * (np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 2]))

# 计算合并后当前区间与后一个区间的卡方值并替换

chi_table[chi_min_index] = (np_regroup[chi_min_index, 1] * np_regroup[chi_min_index + 1, 2] - np_regroup[chi_min_index, 2] * np_regroup[chi_min_index + 1, 1]) ** 2 \

* (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2] + np_regroup[chi_min_index + 1, 1] + np_regroup[chi_min_index + 1, 2]) / \

((np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) * (np_regroup[chi_min_index + 1, 1] + np_regroup[chi_min_index + 1, 2]) * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index + 1, 1]) * (np_regroup[chi_min_index, 2] + np_regroup[chi_min_index + 1, 2]))

chi_table = np.delete(chi_table, chi_min_index + 1, axis=0)

print('已完成卡方分箱核心操作，正在保存结果')


result_data = pd.DataFrame() # 创建一个保存结果的数据框

result_data['variable'] = [variable] * np_regroup.shape[0] # 结果表第一列：变量名

for i in np.arange(np_regroup.shape[0]):

x = '0' + ',' + str(np_regroup[i, 0])

elif i == np_regroup.shape[0] - 1:

x = str(np_regroup[i - 1, 0]) + '+'

x = str(np_regroup[i - 1, 0]) + ',' + str(np_regroup[i, 0])

list_temp.append(x)

result_data['interval'] = list_temp # 结果表第二列：区间

result_data['flag_0'] = np_regroup[:, 2] # 结果表第三列：负样本数目

result_data['flag_1'] = np_regroup[:, 1] # 结果表第四列：正样本数目




bins = ChiMerge(temp, 'x','y', confidenceVal=3.841, bin=10,sample=None)

欢迎访问讲师csdn学院教学主页：https://edu.csdn.net/lecturer/5602，学习更多python金融模型实战。

版权声明：文章来自公众号(python风控模型),未经许可，不得抄袭。遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。