《数字图像处理》第十章 图像分割 学习笔记附部分例子代码(C++ & opencv)

0. 前言

分割将图像细分为构成它的子区域或物体，当感兴趣的物体或区域被检测出来时，就停止其分割。

第三版教材中图片下载地址： DIP 3/e Book Images

vs2019配置opencv可以查看：Opencv的安装与配置(VS 2019 & opencv4.5.4)

代码中出现未知函数，其实现可以查看往期学习笔记

前情回顾：
《数字图像处理》第三章 灰度变换和空间滤波 学习笔记附部分例子代码
《数字图像处理》第四章 频率域滤波 学习笔记附部分例子代码
数字图像处理第五章 图像复原和重建（内容较简单，就没有详细记录笔记）
《数字图像处理》第六章 彩色图像处理 学习笔记附部分例子代码
《数字图像处理》第七章 小波域多分辨率处理 学习笔记附部分例子代码
数字图像处理第八章 图像压缩 非重点
《数字图像处理》第九章 形态学图像处理 学习笔记附部分例子代码

后续剧情：
《数字图像处理》第11章 表示和描述 学习笔记附部分例子代码

1. 基础知识

针对单色图像的分割算法处理灰度值的基于两类特性-不连续性和相似性

• 不连续性，基于边缘的分割是基于灰度的局部不连续性来进行边界检测的

• 相似性，根据事先定义的一组准则把一幅图像分割成相似的几个区域

2. 点、线和边缘检测

本节将集中以灰度局部剧烈变化检测为基础的分割方法上。感兴趣的三种图像特征是孤立点、线和边缘。

2.1 背景知识

局部变化可以通过微分来检测，数字函数的导数使用差分来定义，二维函数中，数字差分使用偏导，所以一阶导表达式：

$$\frac{\partial f}{\partial x}=f^{\prime }(x)=f(x+1)-f(x)$$

二阶导表达式：

$$\frac{{\partial }^{2}f}{\partial x^2}=f^{\prime \prime }(x)=f(x+1)+f(x-1)-2f(x)$$

两种类型的边缘：斜坡边缘（灰度变化较小较稳定）和台阶边缘（灰度值迅速变化，形成“台阶”）
已知的一些结论：

1. 一阶导数通常在图像中产生较粗的边缘

2. 二阶导数对精细细节，如细线和孤立点有较强的响应

3. 二阶导数在灰度斜坡和灰度台阶过渡处会产生双边缘响应

4. 二阶导数的符号可用于确定边缘的过渡是从亮到暗还是从暗到亮

2.1 孤立点的检测

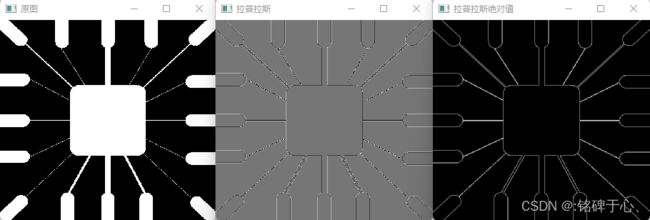
点的检测以二阶导数为基础，故拉普拉斯：

$$\begin{gathered} {\nabla }^{2}f(x,y)=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2} \\ =f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) \end{gathered}$$

如果某点处的二阶响应的绝对值超过某个阈值，那么说明该点被检测到了，置为1，其余点置为0，产生一幅二值图像，数学表达式如下：

$$g(x,y)=\{\begin{array}{cc}1,& |R(x,y)|⩾T\\ 0,& 其他\end{array}$$

void ch10_test01(string path) {
    Mat image = imread(path, IMREAD_GRAYSCALE);
    if (image.empty()) {
        cout << "Unable to load the image\n";
        return;
    }
    //自己定义卷积核
    Mat kernel = (Mat_<float>(3, 3) << 1, 1, 1, 1, -8, 1, 1, 1, 1);

    //卷积
    Mat lap_result;
    filter2D(image, lap_result, CV_32F, kernel);
    lap_result = abs(lap_result);

    double maxValue;
    minMaxLoc(lap_result, NULL, &maxValue);

    Mat thresholded;
    threshold(lap_result, thresholded, 0.9 * maxValue, 255, THRESH_BINARY);

    displayImg(image, "原图");
    displayImg(lap_result, "二阶导数");
    displayImg(thresholded, "二值图");
    waitKey(0);
}

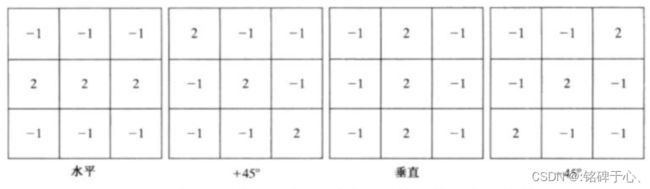
2.2 线检测

检测特定方向的线（垂直方向，水平方向，两个对角方向），每个模版的系数和要为0

2.3 边缘模型

边缘模型根据他们的灰度剖面来分类。

一阶导数的幅度可用于检测图像中的某个点处是否存在一个边缘；二阶导数的符号可以确定一个边缘像素位于该边缘暗的一侧还是亮的一侧。

执行边缘检测的三个基本步骤：

1. 降噪对图像进行平滑处理，因为二阶导数对于噪声非常敏感

2. 边缘点的检测。

3. 边缘定位。

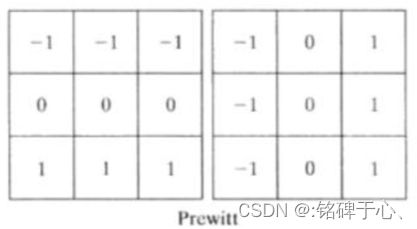
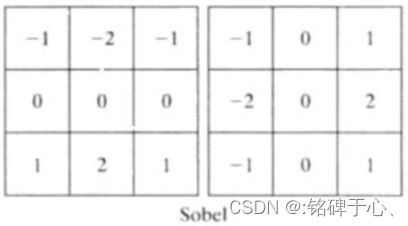
2.4 基本边缘检测

梯度算子：

$$g_x=\frac{\partial f(x,y)}{\partial x}=f(x+1,y)-f(x,y)$$

$$g_y=\frac{\partial f(x,y)}{\partial y}=f(x,y+1)-f(x,y)$$

Prewitt算子：

Sobel算子：

由于平方再开方的计算开销大，所以实际中使用绝对值来近似梯度的幅值，如下所示：

$$M\left(x,y\right)\approx \left|g_x\right|+\left|g_y\right|$$

void ch10_test02(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cout << "Unable to load the image\n";
        return;
    }
    img.convertTo(img, CV_32F);
    normalize(img, img, 0, 1, NORM_MINMAX);

    Mat gradientX;
    Sobel(img, gradientX, CV_32F, 1, 0);
    gradientX = abs(gradientX);
    Mat gradientY;
    Sobel(img, gradientY, CV_32F, 0, 1);
    gradientY = abs(gradientY);

    displayImg(img, "原图02");
    displayImg(gradientX, "x方向梯度|gx|");
    displayImg(gradientY, "y方向梯度|gy|");
    displayImg(gradientX + gradientY, "|gx|+|gy|");
    waitKey(0);
}

计算梯度前对图像进行平滑处理，或者对梯度图像进行阈值处理，可以达到相同的目的——减少精细细节（因为这种细节往往包含有噪声）

2.5 更先进的边缘检测技术

Marr-Hildreth边缘检测算法：

1. 用对式$G(x,y)=e^{\frac{x^2+y^2}{2{\sigma }^2}}$取样得到n×n的高斯低通滤波器对输入图像滤波。

2. 计算由第一步得到的图像的拉普拉斯。

3. 找到步骤2所得到图像的零交叉。

坎尼边缘检测算法：

1. 用一个高斯滤波器平滑输入图像

2. 计算梯度幅值图像和角度图像

3. 对梯度幅值图像应用非最大抑制（最大抑制方案见教材）

4. 用双阀值处理和连接分析来检测并连接边缘

3. 阈值处理

3.1 全局阈值处理

1. 为全局阈值T选择一个初始估计值。
2. 在式（10.3-1）中用7分割该图像。这将产生两组像素：G1由灰度值大于T的所有像素组成, G2由所有小于等于T的像素组成。
3. 对G1和G2的像素分别计算平均灰度值（均值）m1和m2
4. 计算一个新的阈值：$T=\frac{1}{2}(m_1+m_2)$
5. 重复步骤2到步骤4，直到连续迭代中的T值间的差小于一个预定义的参数为止。

3.2 用Otsu方法的最佳全局阈值处理

Otsu算法步骤：

1. 计算输入图像的归一化直方图，使用$p_i$表示。

2. 根据式 $P_1(k) =\sum_{i=0}^{k}p_i $ 计算累计和。

3. 根据式 $m(k)={\sum }_{i=0}^{k}i{p}_i$ 计算累积均值

4. 计算全局灰度均值 $m_G=m(L-1)$

5. 根据式 ${\sigma }_B^2(k)=\frac{(m_G{P}_1-m_k{)}^2}{P_1(1-P_1)}$ 计算类间方差

6. 遍历一整遍，得到类间方差最大时对应的灰度。

//测试函数，Otsu函数的实现在下面
void ch10_test03(string path) {
	Mat image = imread(path, IMREAD_GRAYSCALE);
	if (image.empty()) {
		cout << "unable to load the image\n";
		return;
	}

	Mat binaryImage = Otsu(image);

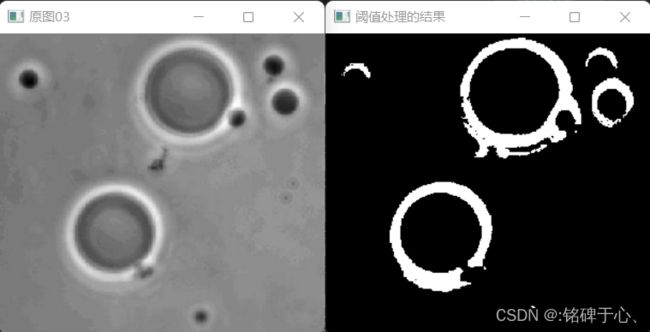
	displayImg(image, "原图03");
	displayImg(binaryImage, "阈值处理的结果");
	waitKey(0);
}

Mat Otsu(Mat input) {
	const int scale = 256;
	int grayNum[scale] = { 0 };
	int r = input.rows;
	int c = input.cols;
	// 直方图统计
	for (int i = 0; i < r; i++) {
		for (int j = 0; j < c; j++) {
			uchar val = input.at<uchar>(i, j);
			grayNum[val]++;
		}
	}
	double totalPixels = r * c;
	double P[scale];
	double Pk[scale];
	double Mk[scale];
	double pkSum = 0, mkSum = 0;
	for (int i = 0; i < scale; i++) {
		P[i] = grayNum[i] / totalPixels;	//每个灰度级出现的概率
		Pk[i] = pkSum + P[i];		//计算累积和Pk
		pkSum = Pk[i];
		Mk[i] = mkSum + i * P[i];	//计算累积均值Mk
		mkSum = Mk[i];
	}
	//计算全局灰度均值Mg，即Mk[scale - 1]
	int bestThre = 0, maxVar = 0;
	for (int i = 0; i < scale; i++) {
		double var = pow(Mk[scale - 1] * Pk[i] - Mk[i], 2);
		var = var / (Pk[i] * (1 - Pk[i]));
		if (var > maxVar) {
			maxVar = var;
			bestThre = i;
		}
	}
	cout << "最佳阈值为" << bestThre << endl;
	Mat binaryImage;
	threshold(input, binaryImage, bestThre, 255, THRESH_BINARY);
	return binaryImage;
}

如果直方图的波峰是高、窄、对称的，且被深的波谷分开，则选取一个"较好的"阈值是有很大机会的。

4. 基于区域的分割

4.1 区域生长

首先需确定相似性准则，当不再有像素满足加入某个区域的准则时，区域就会停止生长。

4.2 区域分裂与聚合

如果直方图的波峰是高、窄、对称的，且被深的波谷分开，则选取一个"较好的"阈值是有很大机会的。

4. 基于区域的分割

4.1 区域生长

首先需确定相似性准则，当不再有像素满足加入某个区域的准则时，区域就会停止生长。

4.2 区域分裂与聚合

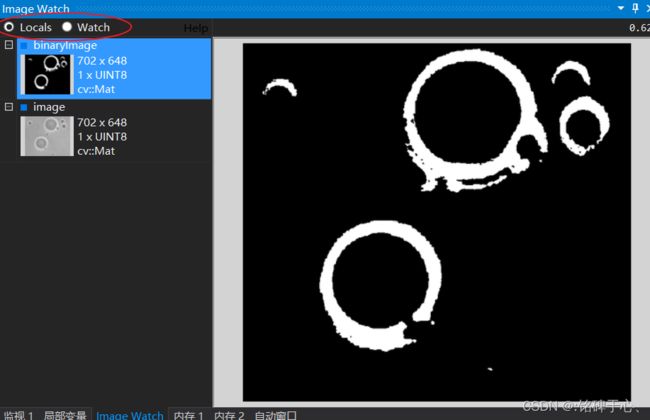
5. 补充：VS添加Image Watch

下载Image Watch插件，Visual Studio 2019 的安装地址 ，下载完成后，双击该.vsix（Visual Studio 扩展）文件，这个时候关闭vs所有进程，就会自动安装完成。

其他版本的vs及使用教程，可以查看OpenCV: Image Watch: viewing in-memory images in the Visual Studio debugger
点击“放大镜”，可以将该Mat加入到“watch”中

分为“local”和“watch”，即局部变量和添加的监视变量