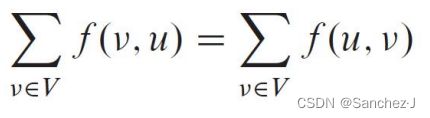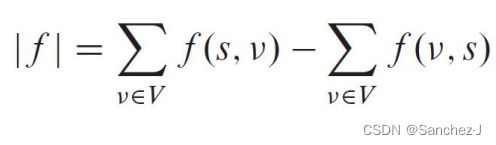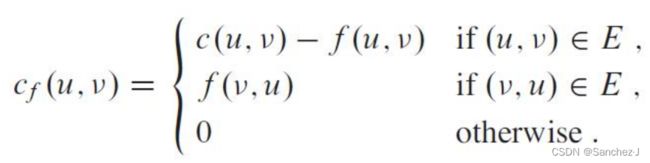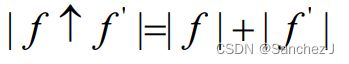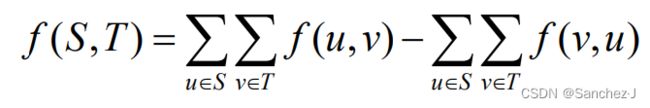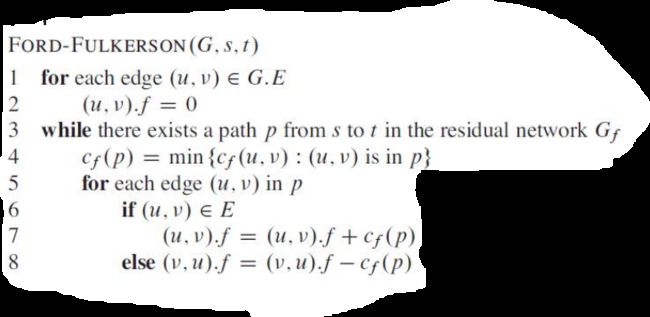算法导论复习——CHP26 最大流

引入

        在物流网络中，从一个城市（称为源结点）发送一批货物到另一个 城市（称为汇点）。假设源结点可以源源不断地提供货物，汇点可以来者不拒地接收货物；路径连接在任意两个城市之间，但路径上有运输容量有限制。货物从源结点到汇点可以选择不同的运输路径。

        问：在不违反任何路径容量限制的条件下，从源结点到汇点运送货物的最大速率是多少——这一问题的抽象称为最大流问题。

        用带权有向图来表示：

•                 结点表示城市
•                 结点间的有向边表示运输路径和物流的方向
•                 边上的权重表示运量限制

        —— 这种用来表示“流”的图称为“流网络”

        约定

        （1）流量守恒：除源结点和汇点外，其它结点上物料只是“流过” ， 即物料进入的速率等于离开的速率，不积累和聚集；

        （2）物料的生成速率和接收速率恒定且足够快、足够多，满足需要；

        （3）每条边上的容量是物料通过该边的最大速率，不能突破。 

        流网络

        流网络是一个有向图 ，边上定义有容量函数：

        (1) 有一个源节点 s 和汇点 t ；

        (2) 有向边表示流向；

        (3) 每条边上有一个非负的容量值 ； 如果 ，为方便起见，定义 

                ；

        (4) 如果边集合E中包含边某边，则图中不包含其反向边 ；

        (5) 图中不允许有自循环；

        (6) 流网络是连通图，每个结点都在从s到t的某条路径上；

        (7) 除源结点外，每个结点至少有一条流入的边；

        (8) 除汇点外，每个结点至少有一条流出的边；

        (9) 

        流

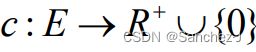        设是一个流网络，其容量函数为。 设s为源结点，t为汇点。 流是定义在G上的一个实值函数，记为 ，并满足以下两条性质：

        （1）容量限制: 对于所有的结点，有

        （2）流量守恒：对于所有结点，有

                这里， f(u,v)称为从结点u到结点v的流。 若 ，记f(u,v) = 0 ,表示从结点u到结点v没有流。

        流的值

        一个流的值定义为流出源结点s的总流量减去流入源结点s 的总流量，用|f |表示：

但通常流网络中没有流入源结点的边。

        最大流

                最大流问题就是在给定的流网络G选中找一个流值最大的流的问题

        一般流网络

        上述定义的流网络有两个标准特性：

        (1)无反向边。

        (2)只有单一的源结点和汇点

        不满足上述要求的流网络这里视为非标准的一般流网络。对于一般流网络需转化为标准流网络进行处理。：

        （1）具有反平行边的流网络转化方法：对每一组反平行边 （u，v）和 （v，u），选择其中的一条， 比如（u，v），然后加入一个新的结点v’ ，将其分为 两条边（u，v'）和（v'，v） ，并将两条新加入的边的容量设为被替代掉的边的容量：c(u,v') = c(v' ,v) = c(u, v）

        （2）具有多个源结点和多个汇点的网络：

                如果流网络中有多个源结点 ：加入一个超级源结点s，并加入有向边 ， 然后令 ；

                如有多个汇点：加入一个超级汇点t，并加入有向边 , 然后令。 

Ford-Fulkerson方法 

        基本思想

        通过不断增加可行流值的方式找到最大流：

        （1）从流值为0的初始流开始；

        （2）通过某种方法，对流值进行增加；

        （3）确认无法再增加流值时，即得到最大流；

          算法步骤

        (1) 对流网络G，在其“残存网络 ”(residual network) 中寻找一条“增广路径p”(augmenting path) 。

        (2) 如果存在增广路径，则对路径上边的流量进行修改，以增加流网络的流量。

        (3) 重复这一过程，直到不再存在增广路径为止。

        判断是否得到最大流的理论基础是最大流最小切割定理，该定理将说明在算法终止时将获得一个最大流。

        残存网络

        对给定流网络G和流量f，G的残存网络 G中的结点和以下的边组成：

        对于G中任意边(u,v)，

        (1) 若 ，则将边(u,v)和它的反向边(v,u)都 加入Gf，并设其“残存容量”为：

                 

                

        残存容量反映了边上可以增加流量的空间

        (2) 如果边(u,v)的流量等于其容量，则，此时(u,v) 不加入Gf ，即只有有多余流量的边才加入Gf。 但仍将反向边(v,u) 加入Gf，并置 。 目的也是为对一个正流量 进行缩减，且最多减少f(u,v)。

        残存容量

        设流网络 ，f 是G中的一个流， 定义边(u,v)的残存容量为：

        残存网络

        由f所诱导的图G的残存网络记为， 其中

        即Gf由残存流量大于0的边构成，且

        残存网络Gf 类似于一个容量为cf的流网络，但Gf不满足流网络的定义：因为Gf可能包含边(u,v)和它的反向边(v,u)。

        但除此之外，残存网络和流网络具有同样的性质。 因此，也可以在残存网络中定义一个流： 设f 是G的一个流，记f' 是残存网络Gf 中的一个流

        f' 针对残存网络Gf中的容量cf定义且满足流的性质( 容量限制、流量守恒 )。

        f' 指出这样一个路线图：如何在原来的流网络中增加流。

        定义为流f'对流f的递增，是一个 从V × V到R的函数：

        在残存网络中将流量发送到反向边上等同于在原来的网络中缩减流量。在残存网络中将流量推送回去称为抵消操作， 其意义在于调整流网络中总流量的分布。

        引理1

        设G=(V,E)为一个流网络，源结点为s，汇点为t。设f为 G 中的一个流。设 Gf 为由流 f 所诱导的G的残存网络， 设 f' 为其中的一个流。那么是G的一个流，其值为

        即：如果在G' 中能够找到一个合法的流f' ，则可以用 f' 对G上原来的流f 进行调整，如果|f' |>0，则可以达到对 f 递增的效果。 

        增广路径

        对给定流网络G=(V,E)和流f ，增广路径p是其残存网络中一条从源结点s到汇点t的简单路径。         根据残存网络的定义，对于增广路径上的一条边(u,v)， 其可增加的流值最大为该边的残存容量 。

        对于一条增广路径p，能增加的最大流值称为该路径的残存容量，等于p上所有边残存容量的最小值。即

                残存容量最小的边是瓶颈，增广路径的流量受其限制。

引理2 

        设G=(V,E)为一个流网络，f 是图G的一个流。记 p 为其残存网络中的一条增广路径。 定义一个函数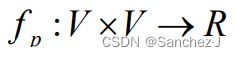如下：

则是残存网络中的一个流。

总结

        如何增加流值——利用增广路径。

        如何判断算法终止时，确实找到了最大流呢？ ——利用最大流最小切割定理进行判定

        最大流最小切割定理：建立最大流和切割容量之间的关系，从而建立最大流和残存网络增广路径上的残存容量之间的关系。

        一个流是最大流当且仅当其残存网络中不包含任何增广路径。

流网络的切割

        给定流网络 ，源结点为s，汇点为t。 定义一个切割(S,T)，将结点集合V分成两部分S和T=V-S， 使得。

        若f是G上的一个流，定义横跨切割(S,T)的净流量f(S,T)为：

        定义切割(S,T)的容量为

        最小切割：一个网络的最小切割是网络中容量最小的切割。

        引理

        设f为流网络G的一个流，该流网络的源结点为s，汇点 为t，设(S,T)为流网络G的任意切割，则横跨切割(S,T) 的净流量为 f (S,T) = | f | 。

        这说明，对流网络的任意切割(S,T)，切割截面上的净流量就等于流网络的流量。 而且，横跨任何切割的净流量都相同，都等于流的值 |f| 。

        推论

        流网络G中任意流f的值不能超过G的任意切割的容量。这说明任何流，包括最大流都不能超过最小切割的容量的限制。

        最大流不可能超过最小切割的容量，那么最大流值是否等于最小切割的容量？确实如此。

        最大流最小割定理

        设f为流网络G=(V,E)中的一个流，该流网络的源结点 为s，汇点为t，则下面的条件是等价的：         （1）f是G的一个最大流

        （2）残存网络 不包括任何增广路径

        （3）| f | = c(S,T )，其中(S,T)是流网络G的某个切割。

        定理说明，流网络G的最大流f在流的值等于任意切割的容量时达到，而此时在对应的残存网络Gf 中不再有增广路径。所以可以用有无增广路径判断当前流f是否是最大 流，如果是，则算法也可以终止了。

算法实现

        

        通过深度优先搜索或者广度优先搜索得到增广路径。

时间复杂度 

        假定：所有的容量均为整数。

        时间复杂度： ， 其中E是流网络的边集， f*是最大流值。

        如边的容量是无理数时，Ford-Fulkerson方法可能不能终止，也就是不会得到最大流。

存在的问题

         时间复杂性与最大流值有关，当最大流值非常大时，效率较低。

Edmonds-Karp算法 

        Edmonds-Karp算法仍然是基于Ford-Fulkerson方法，不同的是使用广度优先搜索寻找源结点到汇点的最短路径作为增广路径（单位距离），从而得到不依赖于最大流值的运行时间上界。

        时间复杂度

应用——最大二分匹配 

        匹配

        对无向图G=(V,E)的一个匹配是边的一个子集 ，使得对于所有的结点v，子集M中最多有一条边与结点v相连。 M中边的数量称为M的基数，记为|M|。

        最大匹配

        基数最大的匹配。

        二分图

        寻找最大二分匹配

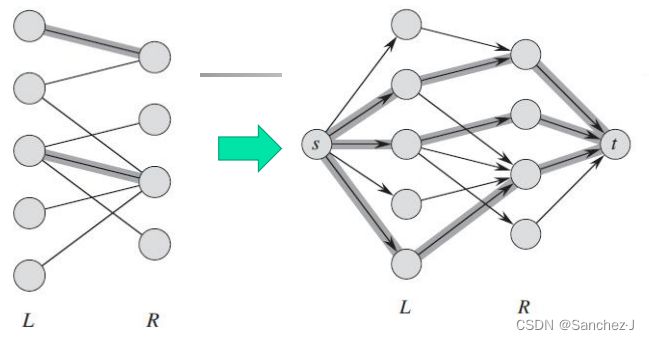
        基本思想：构建一个流网络，将寻找最大二分匹配问题转化为求流网络的最大流问题，流对应于匹配，然后用 Ford-Fulkerson方法寻找最大二分匹配。

                将二分图G所对应的流网络定义如下：

 

 

算法思路

        利用Ford-Fulkerson算法求得G' 中的最大流。流值大于0且在原图中的边将构成最大匹配，而最大匹配的边数就是最大流的流值。 

        时间复杂度