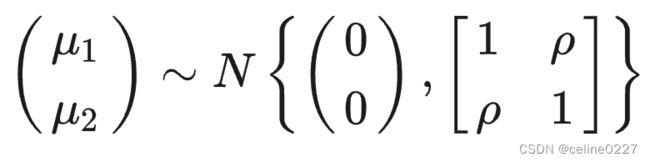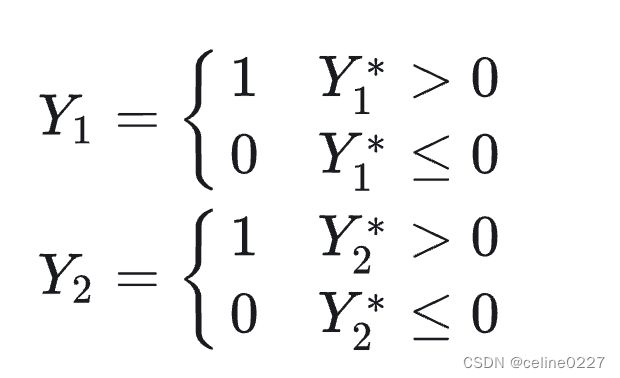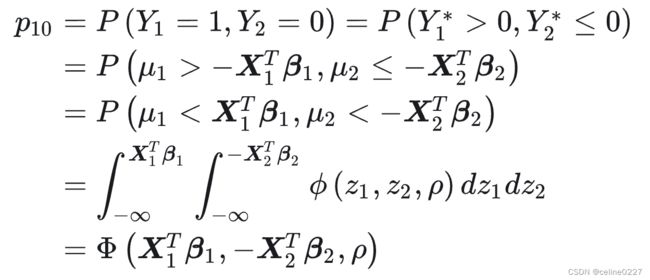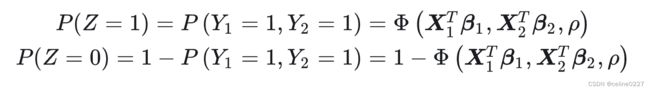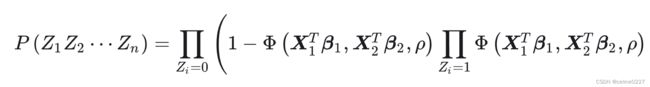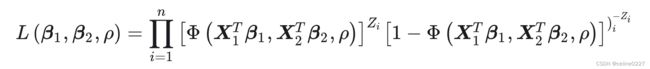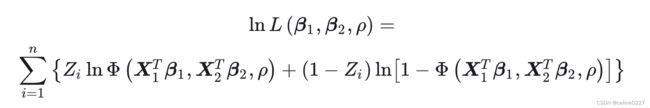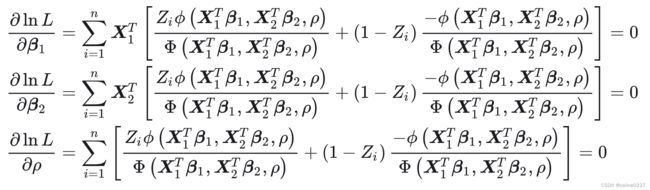双变量probit模型
1. Probit模型
1.1 模型含义
假设个体只有两种选择,y=1或y=0。影响选择的变量都包括在向量x中。即线性概率模型为
![]()
y值服从两点分布
![]()
![]()
![]() 被认为是连接函数,函数选择具有一定的灵活性。如果
被认为是连接函数,函数选择具有一定的灵活性。如果![]() 为标准正态的累积分布函数,则模型成为Probit模型;如果
为标准正态的累积分布函数,则模型成为Probit模型;如果![]() 为逻辑分布的累积分布函数,则为Logit模型。其实,这两种分布函数的公式很相似,函数值相差也并不大,唯一的区别在于逻辑概率分布函数的尾巴比正态分布粗一些。然而,如果因变量是序次变量,回归时只能用有序Probit模型。有序Probit可以看作是Logit的扩展。
为逻辑分布的累积分布函数,则为Logit模型。其实,这两种分布函数的公式很相似,函数值相差也并不大,唯一的区别在于逻辑概率分布函数的尾巴比正态分布粗一些。然而,如果因变量是序次变量,回归时只能用有序Probit模型。有序Probit可以看作是Logit的扩展。
Probit模型是一种服从正态分布的非线性模型,可使用最大似然法进行估计。
1.2 如何衡量二值模型的拟合优度
由于不存在平方和分解公式,故无法计算![]() ,使用由McFadden(1974)提出:
,使用由McFadden(1974)提出:
![]()
其中![]() 为原模型的对数似然函数之最大值,而
为原模型的对数似然函数之最大值,而![]() 为以常数项为唯一解释变量的对数似然函数之最大值。
为以常数项为唯一解释变量的对数似然函数之最大值。
1.2 Probit模型的缺点
Probit回归的偏回归系数含义为,其他自变量保持不变时,该自变量每增加一个单位,出现某个结果的概率密度函数的改变值,这很难以理解。因此Probit模型的回归系数经济意义很难解释,不够直观;而Logistic回归的偏回归系数解释起来更加直观和易于理解,其经济意义也更加明显,所以,一般情况下,Logit模型比Probit模型更简单,应用更广泛。
1.4 可用Probit回归替代Logistic回归的情况
(1)自变量中连续型变量较多。
(2)残差符合正态分布。
2. Bivariate Probit 模型
该模型是Probit模型的拓展,适用于模型中有两个结果变量且假定方程组的随机扰动项之间存在相关性,模型中的方程需同时进行估计。双变量Probit模型是两个二元变量结果的联合模型。如果这两个二元变量的结果是不相关的,我们可以估计两个独立的 Probit 模型,如果这两个二元变量的结果是相关的,使用Probit 模型会导致估计结果偏差并影响结论,则需要使用 Bivariate Probit 模型。比如两个被解释变量,一个是病人是否去看医生,一个是病人是否住院。“看医生”和“住院”两件事通常是相关的,即probit方程的扰动想之间可能存在相关性。
其中,![]() 与
与 ![]() 为不可观测的潜变量, 扰动项
为不可观测的潜变量, 扰动项![]() 服从二维联合正态分布, 期望为 0 , 方差为 1 , 而相关系数为
服从二维联合正态分布, 期望为 0 , 方差为 1 , 而相关系数为 ![]() , 即
, 即
可观测变量 ![]() 与
与 ![]() 由以下方程决定:
由以下方程决定:
当 (24) 式的两个方程的解释变量完全相同, 即 ![]() 时, 即为 “双变量 Probit 模型”。反之, 当两个方程的解释变量不完全相同, 即
时, 即为 “双变量 Probit 模型”。反之, 当两个方程的解释变量不完全相同, 即 ![]() 时, 该模型被称为 “似不相关双变量 Probit 模型”, 因为该模型中两个方程的唯一联系是扰动项的相关性。 若
时, 该模型被称为 “似不相关双变量 Probit 模型”, 因为该模型中两个方程的唯一联系是扰动项的相关性。 若 ![]() =0, 则该模型等价于两个单独的 Probit 模型。当
=0, 则该模型等价于两个单独的 Probit 模型。当 ![]() ≠0 时, 可写下
≠0 时, 可写下![]() 的取值概率, 然后进行最大似然估计。比如:
的取值概率, 然后进行最大似然估计。比如:
其中, ![]() 和
和 ![]() 分别为标准化的二维正态分布的概率密度函数 (PDF) 和累积分布函数 (CDF), 这个标准化的二维正态分布的期望为 0 , 方差为 1 , 而相关系数为
分别为标准化的二维正态分布的概率密度函数 (PDF) 和累积分布函数 (CDF), 这个标准化的二维正态分布的期望为 0 , 方差为 1 , 而相关系数为![]() 。 类似地, 可计算出
。 类似地, 可计算出
对不同的个体计算![]() 的概率, 由此得到所有个体的
的概率, 由此得到所有个体的 ![]() 的概率(这里每一个个体对应的
的概率(这里每一个个体对应的![]() 的概率是唯一的)。将它们全部相乘得到模型的似然函数, 取对数得到对数似然函数, 再由对数似然函数最大化一阶条件可以得到
的概率是唯一的)。将它们全部相乘得到模型的似然函数, 取对数得到对数似然函数, 再由对数似然函数最大化一阶条件可以得到![]() ,
,![]() ,
,![]() 三个方程, 联立它们就可以求解出参数
三个方程, 联立它们就可以求解出参数 ![]() 的值, 当然这也需要数值方法计算得到。最后, 对原假设
的值, 当然这也需要数值方法计算得到。最后, 对原假设![]() 进行检验, 可判断有无必要使用双变量 Probit 模型, 或估 计两个单独的 Probit模型。
进行检验, 可判断有无必要使用双变量 Probit 模型, 或估 计两个单独的 Probit模型。
双变量Probit的stata命令为:
biprobit y1 y2 x1 x2 x3,r (解释变量完全相同)
biprobit (y1=x1 x2)(y2=x1 x3),r nolog (解释变量不完全相同)3. 部分可观测的双变量 Probit 模型
有时候, 我们无法同时观测到 ![]() 与
与![]() , 而只能看到
, 而只能看到 ![]() 与
与![]() 都取值为 1 的情况。比如, 估计实习生在某公司实习后留任的概率。显然, “留任” 既取决于该公司是否向该实习生发聘书 (公司的二值选择), 也取决于该实习生是否愿意在此公司工作 (实习生的二值选择)。 而我们只能观测到该实习生是否留任了。如果留任, 则
都取值为 1 的情况。比如, 估计实习生在某公司实习后留任的概率。显然, “留任” 既取决于该公司是否向该实习生发聘书 (公司的二值选择), 也取决于该实习生是否愿意在此公司工作 (实习生的二值选择)。 而我们只能观测到该实习生是否留任了。如果留任, 则![]() 与
与 ![]() 都取值为 1; 如果末留任, 则只知道
都取值为 1; 如果末留任, 则只知道![]() 与
与 ![]() 至少有一个为 0。在此情况下, 公司的二值选择与实习生的二值选择可能相关, 故适用于双变量 Probit 模型的框架。但对于
至少有一个为 0。在此情况下, 公司的二值选择与实习生的二值选择可能相关, 故适用于双变量 Probit 模型的框架。但对于 ![]() 与
与![]() 只有其乘积
只有其乘积 ![]() ⋅
⋅![]() 可观测, 要么
可观测, 要么 ![]() 或
或![]() ,此时定义
,此时定义![]()
我们对 ![]() 做最大似然估计
做最大似然估计
参数![]() 的对数似然函数的最大化一阶条件分别为
的对数似然函数的最大化一阶条件分别为
biprobit (y1=x1 x2)(y2=x1 x3),r partial difficult
partial表示部分可观测的双变量probit,但加上这个选择后可能使得数值计算不收敛。如果不收敛,可使用difficult表示在最大化目标函数存在非凹区域的情况下,使用另一种迭代方法。
在实际中我们只能观测到![]() ,记
,记![]() ,定义
,定义![]() 然后再进行估计
然后再进行估计
gen z2=z1
biprobit(z1 =x1 x2)(z2=x1 x3),r partial difficult nolog3.1 模型的优势
(1)双变量Probit模型能够解决两个方程间的内在联系问题,提高估计的效率。
(2)双变量Probit模型是解决对两个虚拟变量同时考虑其发生的概率的模型,当两个Probit方程的扰动项之间可能存在相关性,如果对这两个被解释变量分别进行建模,则估计结果会损失效率。也就是说当对两个相关的被解释变量进行研究时,比如上述提到的“看医生”和“住院”这两件相关联的事情,就可以使用双变量Probit模型,避免估计结果效率的损失,使估计结果更为准确。
3.2 模型的缺点
(1)双变量Probit模型必须假设随机变量服从正态分布,相比与Logit模型,没有那么简单直接,应用更窄。
(2)假设条件比较严格,计算过程复杂,且有较多近似处理。
(3)在现实经济中,经济主体无法同时观测到y1和y2,只能观察到同时为1的情况。比如,估计实习生在某公司实习后留任的概率。我们一般只能观测到该实习生是否留任。
(4)存在稀有事件偏差。虽然使用MLE(比如Probit 或Logit)来估计二值选择模型是一致的,但在有限样本下(样本容量小于200) , Probit或Logit估计依然存在偏差。而且,如果存在稀有事件,则该偏差将进一步放大;导致即使样本容量达到数千,而偏差依然存在,称为“稀有事件偏差( rare event bias)”。例如战争、政变、革命、流行病、经济危机、百年一遇的灾害等。