机器学习周报第九周

摘要

RNN通过引入门控机制（如LSTM和GRU）来解决梯度消失和梯度爆炸问题。通过LSTM可以在时间步骤中保存和更新重要信息，同时抑制不重要的信息，从而减缓梯度的变化，有效地解决了梯度消失和梯度爆炸问题。Transformer是一种基于注意力机制的模型，特别适用于处理序列数据。它采用了编码器-解码器结构，其中编码器部分负责将输入序列编码为特征表示，解码器部分负责将特征表示转换为输出序列。Transformer的编码器由多层的自注意力层和全连接前馈层组成。自注意力层通过计算输入序列中各元素之间的关联性来捕捉长距离的依赖关系。而在计算注意力权重时，Transformer使用了缩放点积注意力机制，使得模型能够高效处理长序列。

Abstract

RNN solves the gradient vanishing and gradient explosion problems by introducing gating mechanisms such as LSTM and GRU. With LSTM it is possible to save and update important information in time steps while suppressing unimportant information, thus slowing down the gradient change and effectively solving the gradient vanishing and gradient explosion problems.Transformer is a model based on the attention mechanism, which is particularly suitable for processing sequence data. It adopts an encoder-decoder structure, in which the encoder part is responsible for encoding the input sequences into feature representations and the decoder part is responsible for converting the feature representations into the output sequences.Transformer’s encoder consists of a multilayered self-attention layer and a fully-connected feedforward layer. The self-attention layer captures long range dependencies by calculating the correlation between the elements in the input sequence. And in computing the attention weights, Transformer uses a scaled dot product attention mechanism, which enables the model to efficiently handle long sequences.

一、循环神经网络

1.存在的问题

在训练RNN模型的过程中，损失函数随着epoch的增大并不会像下图中蓝色曲线那样平滑地下降，而是像绿色的曲线那样产生剧烈的抖动。如下图所示。

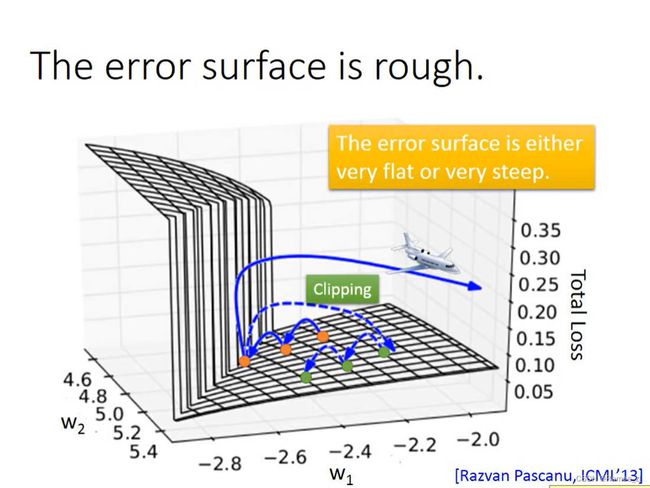
产生以上状况的原因如下图所示。RNN的损失函数的曲面在有些地方是很平坦的，但是有些地方又非常崎岖，所以会造成损失函数剧烈抖动的情况。
当训练的起始点在平坦的曲面上时，随着训练次数的增多，训练后的点可能会在“悬崖”或者“峭壁”上。如果该点在“悬崖”上，那么会出现上图中损失函数暴增的情况，即产生了梯度爆炸；如果该点正好被训练到“峭壁”之上，由于该点的梯度很大，而且之前在平坦的曲面上训练，所以设置的学习率会较大，所以在该点后的下一次训练会由于过大而“飞”出去。

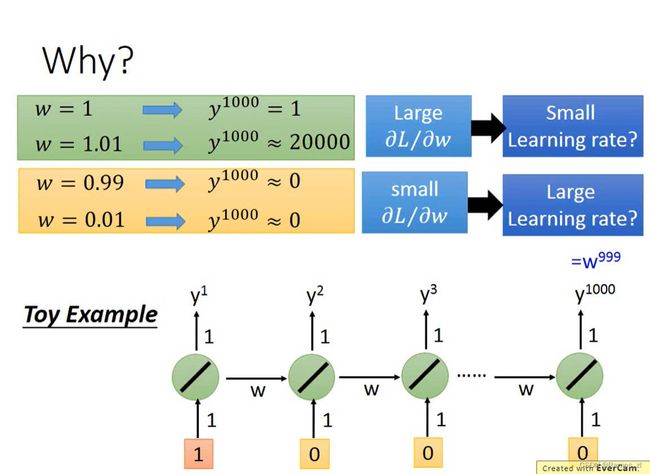
下图使用一个简单的模型来解释RNN在训练的时候的损失函数会发生震荡的原因。该模型输入的weight和输出的weight都是1，transition的weight全是w。在该模型中有1000个神经元。所以$y^{1000}$的输出时$w^{999}$。当$w=1$时，$y^{1000}=1$。但是，如果$w$的值产生微小的变化，会对整个输出的值产生非常大的影响，从而造成损失函数曲线的震荡。当$w=1.01$时，$y^{1000}=20000$，而当$w=0.99$时，$y^{1000}=0$。

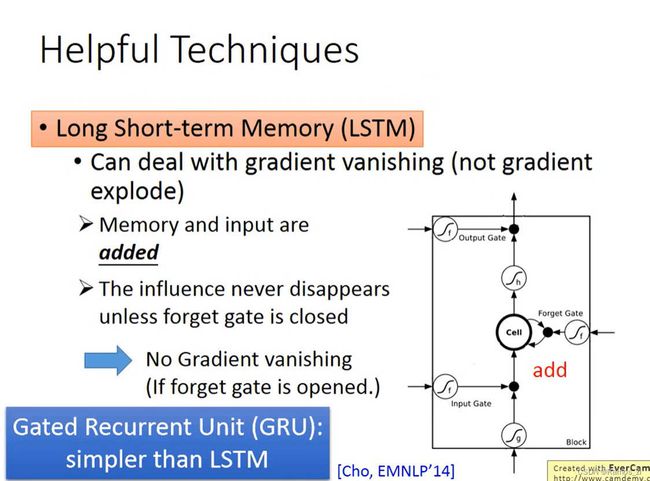
可以使用LSTM来解决RNN的梯度爆炸和梯度消失的问题。在传统的RNN中，梯度消失的问题是由于反向传播过程中，梯度在时间步上指数级地衰减，导致较早的时间步的信息无法有效地传递到后面的时间步，从而难以捕捉长期依赖关系。这是因为在传统RNN中，隐藏状态的更新是通过简单的线性组合和非线性激活函数来实现的，使得梯度在反向传播时容易消失。而LSTM的门控机制使得LSTM能够在更新隐藏状态时选择性地保留和遗忘信息，从而有效地捕捉长期依赖关系。门控机制的引入使得梯度能够在反向传播过程中得到更好的传递，从而缓解了梯度消失问题。
在控制梯度爆炸的问题上，LSTM中引入的门控机制，特别是遗忘门，可以帮助控制梯度的传播并防止梯度爆炸。遗忘门的作用是根据当前输入和前一时刻的隐藏状态来决定是否遗忘之前的信息。这样，LSTM能够选择性地保留重要的信息，并且将梯度值保持在合理的范围内。

二、RNN的应用

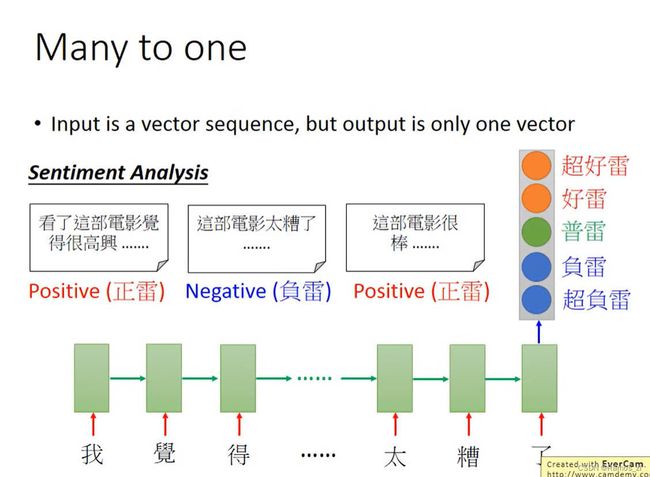
1.评价类型分析
通过输入用户的评价来判断该评价的类型。

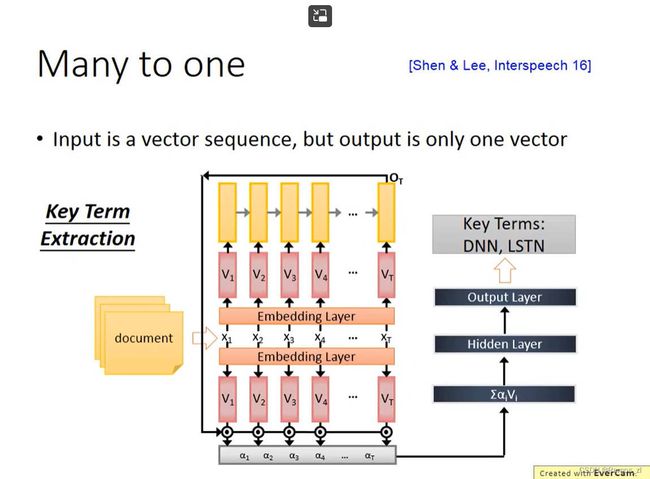
2.寻找文章的关键词
将文件的内容转化成向量作为下图模型的输入，输出是该文件的关键词。

3.语音辨识
将语音信息转化为一个个向量输入模型，输出是该语音对应的文字。可以使用CTC的技术来控制输出。即使用一个特殊的符号来代替“NULL”

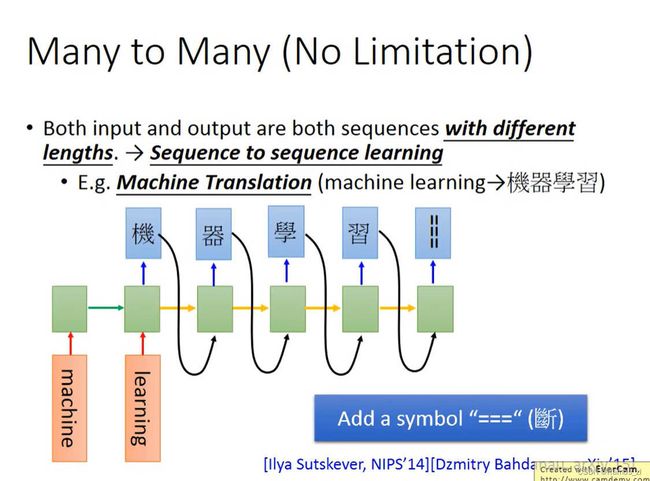
4.机器翻译
如下图所示，将"machine learning"作为模型的输入，然后将RNN最后一个输出作为下一个输入，在输出的最后加入特殊符号结束输出。

5.句法分析
将句子的各个结构用树状图表示。

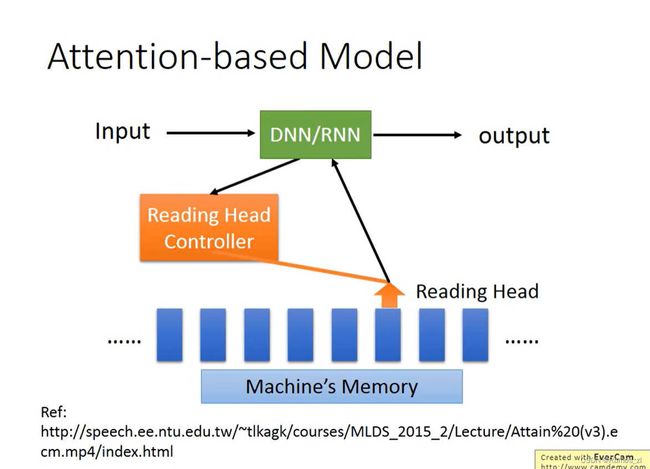
6.基于注意力的模型
该模型有较大的内存来存储信息。每次将输入输入到中央处理器，由中央处理器操控reading head controller在内存中读取相关的内容，将其取出放入中央处理器中再输出结果。

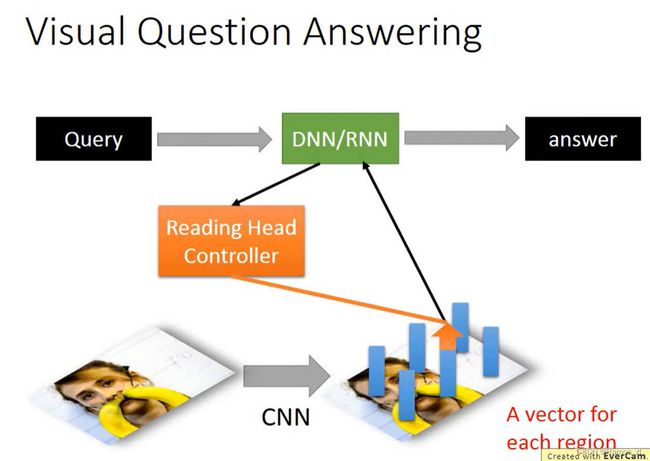
7.视觉问题解答
使用CNN将图片的每个区域转化成一个个向量，将问题输入模型，中央处理器通过操控reading head controller在向量中寻找合适的向量，最后得到答案。

三、transformer

3.1 seq2seq

Seq2Seq（Sequence-to-Sequence）是一种用于处理序列到序列（seq2seq）任务的深度学习模型。它最初被广泛应用于机器翻译任务，但后来也被用于其他自然语言处理任务，如文本摘要、对话生成等。

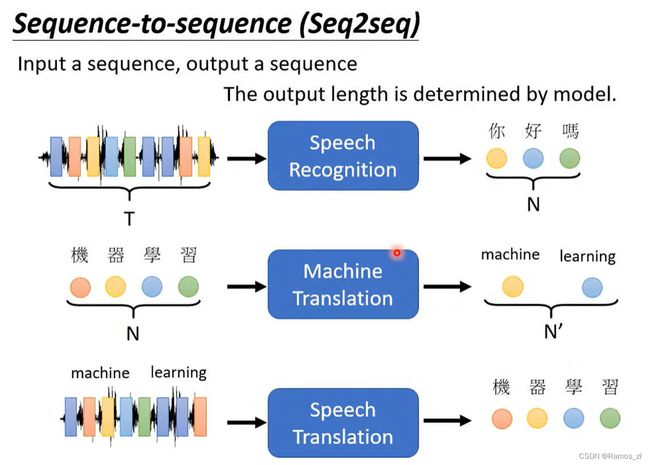
Seq2Seq模型由两个主要部分组成：编码器（Encoder）和解码器（Decoder）。编码器负责将输入序列转换为一个固定维度的上下文向量（context vector），并捕捉输入序列的语义信息。解码器则根据这个上下文向量，逐步生成目标序列。

在seq2seq模型架构中，由多个block嵌套而成。输入经过一个block后的输出再作为下一个block的输入，如此重复多次。而一个block由一个自注意力机制的架构组成。输入经过一个self-attention层，再将该层的输出放入一个fully-connected layer中，得到的输出即一个block的输出。

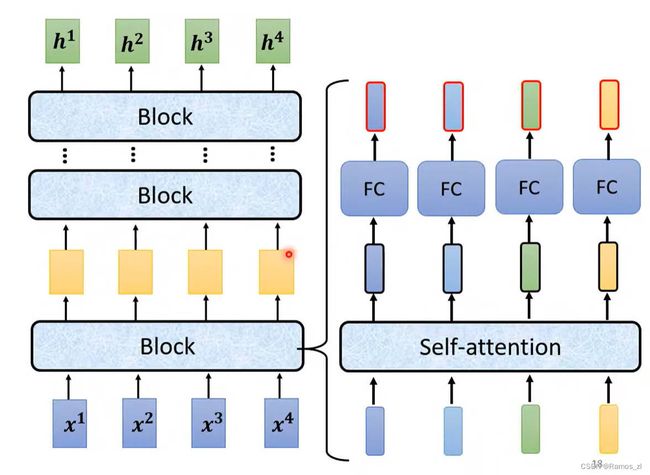
在tramsformer的block中还有一些处理上的细节。在self-attention的输出还需要进行残差(residual)的操作，再对该操作的结果进行layer norm才可以将该输出放入fully-connected layer中。fully-connected layer还需要进行一个residual和放入layer norm操作后，得到的输出才是整个block的完整输出。

四、线性模型

import random
import torch
from d2l import torch as d2l
import matplotlib.pyplot as plt


# 根据一个有噪音的线性模型得到一个数据集
def synthetic_data(w, b, num_examples):
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape(-1, 1)


true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print(f'features:{features[0]},labels:{labels[0]}')

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy())
plt.show()


# 读取数据集
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]


batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

# 初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)


# 定义模型
def linreg(X, w, b):
    return torch.matmul(X, w) + b


# 定义损失函数
def squared_loss(y_hat, y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2


# 定义优化算法
def sgd(params, lr, batch_size):
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

输出如下：
epoch 1, loss 0.030206
epoch 2, loss 0.000113
epoch 3, loss 0.000051
w的估计误差: tensor([ 0.0002, -0.0001], grad_fn=)
b的估计误差: tensor([9.2983e-05], grad_fn=)

五、softmax回归

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

accuracy(y_hat, y) / len(y)

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

evaluate_accuracy(net, test_iter)

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

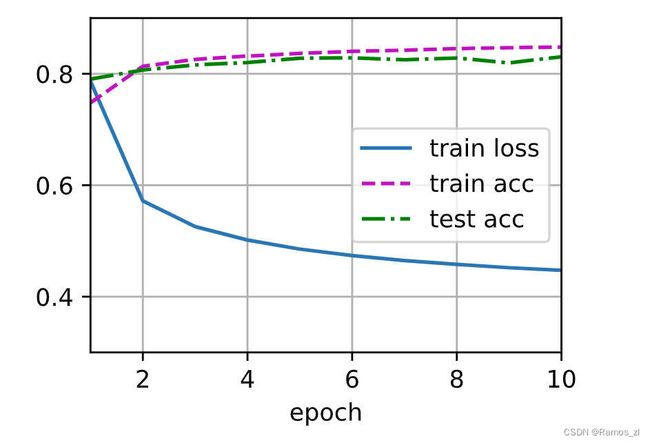
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

输出如下：

总结

RNN通过门控机制解决梯度消失和梯度爆炸问题，而Transformer通过注意力机制提高了对长序列的建模能力，并能高效处理序列数据，这两种模型在自然语言处理、机器翻译和语音识别等领域都取得了显著的进展。下周我将继续进行Transformer和代码的学习。