【机器学习】循环神经网络(二)-LSTM示例(keras)国际航空乘客问题的回归问题...
使用 Keras 在 Python 中使用 LSTM 循环神经网络进行时间序列预测
国际航空乘客问题的回归问题
这个文件是一个CSV格式的数据集,它包含了从1949年1月到1960年12月的每个月的国际航空乘客的总数(以千为单位)。第一行是列名,分别是"Month"和"International airline passengers: monthly totals in thousands. Jan 49 ? Dec 60"。第一列是每个月的日期,格式是"年份-月份"。第二列是每个月的乘客总数,单位是千人。这个数据集可以用来训练一个LSTM模型,来预测未来的乘客数量。LSTM是一种循环神经网络,它可以利用长期的时间序列信息来进行预测。
"Month","International airline passengers: monthly totals in thousands. Jan 49 ? Dec 60"
"1949-01",112
"1949-02",118
"1949-03",132
"1949-04",129
"1949-05",121
"1949-06",135
"1949-07",148
"1949-08",148
"1949-09",136
"1949-10",119
"1949-11",104
"1949-12",118
"1950-01",115
"1950-02",126
"1950-03",141
"1950-04",135
"1950-05",125
"1950-06",149
"1950-07",170
"1950-08",170
"1950-09",158
"1950-10",133
"1950-11",114
"1950-12",140
"1951-01",145
"1951-02",150
"1951-03",178
"1951-04",163
"1951-05",172
"1951-06",178
"1951-07",199
"1951-08",199
"1951-09",184
"1951-10",162
"1951-11",146
"1951-12",166
"1952-01",171
"1952-02",180
"1952-03",193
"1952-04",181
"1952-05",183
"1952-06",218
"1952-07",230
"1952-08",242
"1952-09",209
"1952-10",191
"1952-11",172
"1952-12",194
"1953-01",196
"1953-02",196
"1953-03",236
"1953-04",235
"1953-05",229
"1953-06",243
"1953-07",264
"1953-08",272
"1953-09",237
"1953-10",211
"1953-11",180
"1953-12",201
"1954-01",204
"1954-02",188
"1954-03",235
"1954-04",227
"1954-05",234
"1954-06",264
"1954-07",302
"1954-08",293
"1954-09",259
"1954-10",229
"1954-11",203
"1954-12",229
"1955-01",242
"1955-02",233
"1955-03",267
"1955-04",269
"1955-05",270
"1955-06",315
"1955-07",364
"1955-08",347
"1955-09",312
"1955-10",274
"1955-11",237
"1955-12",278
"1956-01",284
"1956-02",277
"1956-03",317
"1956-04",313
"1956-05",318
"1956-06",374
"1956-07",413
"1956-08",405
"1956-09",355
"1956-10",306
"1956-11",271
"1956-12",306
"1957-01",315
"1957-02",301
"1957-03",356
"1957-04",348
"1957-05",355
"1957-06",422
"1957-07",465
"1957-08",467
"1957-09",404
"1957-10",347
"1957-11",305
"1957-12",336
"1958-01",340
"1958-02",318
"1958-03",362
"1958-04",348
"1958-05",363
"1958-06",435
"1958-07",491
"1958-08",505
"1958-09",404
"1958-10",359
"1958-11",310
"1958-12",337
"1959-01",360
"1959-02",342
"1959-03",406
"1959-04",396
"1959-05",420
"1959-06",472
"1959-07",548
"1959-08",559
"1959-09",463
"1959-10",407
"1959-11",362
"1959-12",405
"1960-01",417
"1960-02",391
"1960-03",419
"1960-04",461
"1960-05",472
"1960-06",535
"1960-07",622
"1960-08",606
"1960-09",508
"1960-10",461
"1960-11",390
"1960-12",432
International airline passengers: monthly totals in thousands. Jan 49 ? Dec 60长短时记忆网络(LSTM)
长短时记忆网络(Long Short-Term Memory network,LSTM网络)是使用通过时间反向传播进行训练的循环神经网络,它克服了梯度消失问题。
因此,它可用于创建大型循环网络,进而可用于解决机器学习中的困难序列问题,并取得最先进的结果。
与神经元不同,LSTM网络通过层连接的记忆块。
一个块具有使其比经典神经元更智能的组件以及用于最近序列的记忆。一个块包含管理块状态和输出的门。块对输入序列进行操作,块内的每个门使用Sigmoid激活单元来控制它是否被触发,从而使块的状态变化和通过块的信息添加成为有条件的。
在一个单元内有三种类型的门:
遗忘门(Forget Gate): 有条件地决定从块中丢弃哪些信息
输入门(Input Gate): 有条件地决定从输入中更新内存状态的哪些值
输出门(Output Gate): 有条件地决定基于输入和块的记忆输出什么
每个单元都像一个小型状态机,其中单元的门具有在训练过程中学到的权重。
您可以看到如何通过LSTM层实现复杂的学习和记忆,并且不难想象如何通过多个这样的层堆叠多层高阶抽象。
1. LSTM网络用于回归 用一个步长预测一个,监督学习数据类型1->1
您可以将问题表述为回归问题。
也就是说,给定本月的乘客数(以千为单位),下个月的乘客数是多少?
您可以编写一个简单的函数将单列数据转换为两列数据集:第一列包含本月(t)的乘客数,第二列包含要预测的下个月(t+1)的乘客数。
用 Python 和 Keras 实现的长短期记忆网络(LSTM)的源代码,用于解决国际航空乘客问题的回归问题。
# 导入所需的模块
import numpy # 用于进行科学计算
import matplotlib.pyplot as plt # 用于进行数据可视化
from pandas import read_csv # 用于读取 CSV 文件
import math # 用于进行数学运算
from keras.models import Sequential # 用于构建顺序模型
from keras.layers import Dense # 用于构建全连接层
from keras.layers import LSTM # 用于构建长短期记忆网络层
from sklearn.preprocessing import MinMaxScaler # 用于进行数据缩放
from sklearn.metrics import mean_squared_error # 用于计算均方误差
"""
用一个步长预测一个,监督学习数据类型1->1
X Y
112 118
118 132
132 129
129 121
121 135
"""
# 定义一个函数,将数据截取成1->1的监督学习格式
def create_dataset(dataset, look_back=1):
dataX, dataY = [], [] # 初始化输入和输出的空列表
for i in range(len(dataset)-look_back-1): # 循环遍历数据集,除去最后一个步长和最后一个元素
a = dataset[i:(i+look_back), 0] # 取出当前位置到下一个步长的数据,作为输入
dataX.append(a) # 将输入添加到输入列表中
dataY.append(dataset[i + look_back, 0]) # 取出下一个步长的数据,作为输出
return numpy.array(dataX), numpy.array(dataY) # 将输入和输出列表转换为 numpy 数组,并返回
# 定义随机种子,以便重现结果
numpy.random.seed(7)
# 加载数据
dataframe = read_csv('LSTM\\LSTM_Fly\\airline-passengers.csv', usecols=[1], engine='python') # 读取 CSV 文件,只使用第二列(乘客数)的数据
dataset = dataframe.values # 将数据框转换为 numpy 数组
dataset = dataset.astype('float32') # 将数据类型转换为浮点数
# 缩放数据
scaler = MinMaxScaler(feature_range=(0, 1)) # 创建一个数据缩放器,将数据缩放到 0 到 1 的范围
dataset = scaler.fit_transform(dataset) # 对数据集进行缩放,并返回缩放后的数据集
# 分割2/3数据作为训练集,剩余的作为测试集
train_size = int(len(dataset) * 0.67) # 计算训练集的大小,为数据集长度的 2/3
test_size = len(dataset) - train_size # 计算测试集的大小,为数据集长度减去训练集的大小
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] # 将数据集分割为训练集和测试集,分别为前 2/3 和后 1/3 的数据
# 预测数据步长为1,一个预测一个,1->1
look_back = 1 # 定义预测数据的步长为 1,即用一个数据预测下一个数据
trainX, trainY = create_dataset(train, look_back) # 调用 create_dataset 函数,将训练集转换为 1->1 的监督学习格式,得到训练集的输入和输出
testX, testY = create_dataset(test, look_back) # 调用 create_dataset 函数,将测试集转换为 1->1 的监督学习格式,得到测试集的输入和输出
# 重构输入数据格式 [samples, time steps, features] = [95,1,1]
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1])) # 将训练集的输入重构为三维数组,第一维为样本数,第二维为时间步数,第三维为特征数,分别为 95,1,1
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1])) # 将测试集的输入重构为三维数组,第一维为样本数,第二维为时间步数,第三维为特征数,分别为 46,1,1
# 构建 LSTM 网络
model = Sequential() # 创建一个顺序模型
model.add(LSTM(4, input_shape=(1, look_back))) # 向模型中添加一个 LSTM 层,设置 LSTM 单元的数量为 4,输入的形状为 (1, 1),即一个时间步,一个特征
model.add(Dense(1)) # 向模型中添加一个全连接层,设置输出的维度为 1,即一个预测值
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型,设置损失函数为均方误差,优化器为 adam
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2) # 训练模型,设置迭代次数为 100,批量大小为 1,显示训练过程
# 对训练数据的Y进行预测
trainPredict = model.predict(trainX) # 调用模型的 predict 方法,对训练集的输入进行预测,得到训练集的预测值
# 对测试数据的Y进行预测
testPredict = model.predict(testX) # 调用模型的 predict 方法,对测试集的输入进行预测,得到测试集的预测值
# 对数据进行逆缩放
trainPredict = scaler.inverse_transform(trainPredict) # 调用数据缩放器的 inverse_transform 方法,对训练集的预测值进行逆缩放,得到原始的乘客数
trainY = scaler.inverse_transform([trainY]) # 调用数据缩放器的 inverse_transform 方法,对训练集的输出进行逆缩放,得到原始的乘客数
testPredict = scaler.inverse_transform(testPredict) # 调用数据缩放器的 inverse_transform 方法,对测试集的预测值进行逆缩放,得到原始的乘客数
testY = scaler.inverse_transform([testY]) # 调用数据缩放器的 inverse_transform 方法,对测试集的输出进行逆缩放,得到原始的乘客数
# 计算RMSE误差
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0])) # 调用 sklearn 的 mean_squared_error 函数,计算训练集的真实值和预测值之间的均方误差,然后开平方,得到训练集的均方根误差
print('Train Score: %.2f RMSE' % (trainScore)) # 打印训练集的均方根误差
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0])) # 调用 sklearn 的 mean_squared_error 函数,计算测试集的真实值和预测值之间的均方误差,然后开平方,得到测试集的均方根误差
print('Test Score: %.2f RMSE' % (testScore)) # 打印测试集的均方根误差
# 构造一个和dataset格式相同的数组,共145行,dataset为总数据集,把预测的93行训练数据存进去
trainPredictPlot = numpy.empty_like(dataset) # 创建一个和数据集形状相同的空数组,用于存放训练集的预测值
# 用nan填充数组
trainPredictPlot[:, :] = numpy.nan # 将数组的所有元素填充为 nan
# 将训练集预测的Y添加进数组,从第1位到第95+1位,共95行
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# 这一行的作用是将训练集的预测值插入到 trainPredictPlot 数组中,以便于和原始数据集进行对比。由于我们的预测数据步长为 1,所以我们需要从第 1 位开始,到第 95+1 位结束,共 95 行。注意,这里的索引是从 0 开始的,所以第 1 位实际上是第 2 个元素。
# 构造一个和 dataset 格式相同的数组,共144行,把预测的后46行测试数据数据放进去
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
# 这两行的作用是创建一个和数据集形状相同的空数组,用于存放测试集的预测值,并将所有元素填充为 nan,表示空缺。
# 将测试集预测的Y添加进数组,从第95+1位到最后,共46行 #look_back * 2 为了让训练集预测线条与测试集预测线条分开
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# 这一行的作用是将测试集的预测值插入到 testPredictPlot 数组中,以便于和原始数据集进行对比。由于我们的预测数据步长为 1,所以我们需要从第 95+1 位开始,到最后一位结束,共 46 行。注意,这里的索引是从 0 开始的,所以第 95+1 位实际上是第 98 个元素,最后一位实际上是第 144 个元素。
#print(testPredictPlot.shape[1]) 1
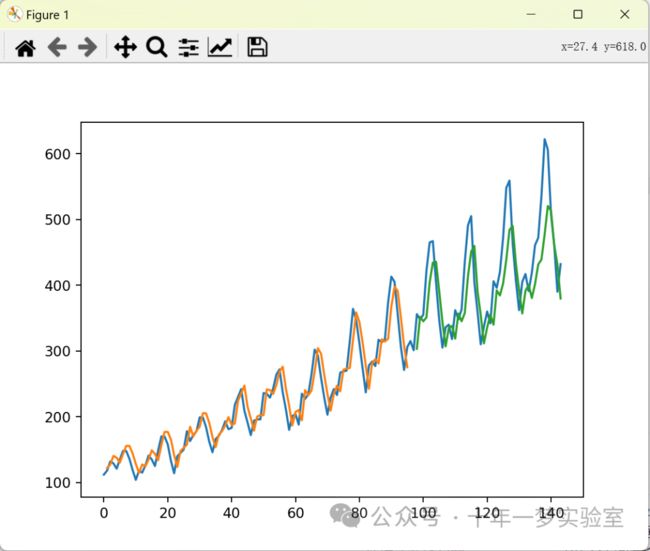
# 画图
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
# 这四行的作用是使用 matplotlib.pyplot 模块绘制图形,显示原始数据集,训练集的预测值,和测试集的预测值。由于我们之前对数据集进行了缩放,所以我们需要先用数据缩放器的 inverse_transform 方法将数据恢复到原始的范围。然后,我们分别用 plt.plot 函数绘制三条曲线,分别用不同的颜色表示。最后,我们用 plt.show 函数显示图形。运行输出:
……
Epoch 94/100
95/95 - 0s - loss: 0.0020 - 258ms/epoch - 3ms/step
Epoch 95/100
95/95 - 0s - loss: 0.0021 - 263ms/epoch - 3ms/step
Epoch 96/100
95/95 - 0s - loss: 0.0020 - 276ms/epoch - 3ms/step
Epoch 97/100
95/95 - 0s - loss: 0.0020 - 295ms/epoch - 3ms/step
Epoch 98/100
95/95 - 0s - loss: 0.0021 - 279ms/epoch - 3ms/step
Epoch 99/100
95/95 - 0s - loss: 0.0020 - 265ms/epoch - 3ms/step
Epoch 100/100
95/95 - 0s - loss: 0.0020 - 271ms/epoch - 3ms/step
Train Score: 22.96 RMSE
Test Score: 52.15 RMSE2. 用三个步长数据预测一个数据 1个时间步长 3个特征 预测1个数据
如何使用窗口方法(Window Method)构建回归问题,使得可以利用多个最近的时间步长来预测下一个时间步长的值。
窗口方法是指将问题表述为使用多个最近的时间步长进行预测,而窗口的大小是一个可以为每个问题调整的参数。
举例来说,假设给定当前时间(t)来预测序列中下一个时间点(t+1)的值,可以将当前时间(t)以及两个先前的时间点(t-1和t-2)作为输入变量。当将其表述为回归问题时,输入变量为t-2、t-1和t,而输出变量为t+1。
在先前部分创建的create_dataset()函数允许通过将look_back参数从1增加到3来创建这种形式的时间序列问题。
示例数据集的一部分如下所示:
X1 X2 X3 Y
112 118 132 129
118 132 129 121
132 129 121 135
129 121 135 148
121 135 148 148通过使用较大的窗口大小,可以重新运行先前部分的示例。以下是带有窗口大小更改的完整代码清单,以便更好地理解。
# 修改 create_dataset() 函数的 look_back 参数
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)通过这样的修改,你就可以使用更大的窗口来构建时间序列回归问题,从而利用多个最近的时间步长进行预测
# LSTM 用于国际航班乘客问题的窗口回归框架
import numpy # 导入 numpy 库,用于处理数组和矩阵
import matplotlib.pyplot as plt # 导入 matplotlib 库,用于绘制图形
from pandas import read_csv # 导入 pandas 库,用于读取和处理 csv 文件
import math # 导入 math 库,用于进行数学运算
from keras.models import Sequential # 导入 keras 库,用于构建和训练神经网络
from keras.layers import Dense # 导入 keras.layers 库,用于添加全连接层
from keras.layers import LSTM # 导入 keras.layers 库,用于添加长短期记忆(LSTM)层
from sklearn.preprocessing import MinMaxScaler # 导入 sklearn.preprocessing 库,用于对数据进行最小最大缩放
from sklearn.metrics import mean_squared_error # 导入 sklearn.metrics 库,用于计算均方误差(MSE)
import pandas as pd # 导入 pandas 库,用于处理数据框
"""
用三个步长数据预测一个数据,数据类型:
X1 X2 X3 Y
112 118 132 129
118 132 129 121
132 129 121 135
129 121 135 148
121 135 148 148
数据形状:
x -> y = [93,1,3] -> [93,1]
x = [[[x1,x2,x3]],
[[x1,x2,x3]],
[[x1,x2,x3]],
...]
y = [[y1],
[y2],
[y3],
...]
input_shape=(1,3)
代码变动部分:
look_back = 3
"""
pd.set_option('display.max_columns',1000) # 设置 pandas 的显示选项,使得最多显示 1000 列
pd.set_option('display.width', 1000) # 设置 pandas 的显示选项,使得每行的宽度为 1000
pd.set_option('display.max_colwidth',1000) # 设置 pandas 的显示选项,使得每列的最大宽度为 1000
# 将数据截取成3个一组的监督学习格式
def create_dataset(dataset, look_back=1): # 定义一个函数,用于将数据转换为监督学习的格式
dataX, dataY = [], [] # 初始化两个空列表,用于存储输入和输出数据
for i in range(len(dataset)-look_back-1): # 遍历数据集,从第一个元素到倒数第 look_back+1 个元素
a = dataset[i:(i+look_back), 0] # 取出当前位置到当前位置加上 look_back 的数据,作为输入
dataX.append(a) # 将输入数据添加到 dataX 列表中
dataY.append(dataset[i + look_back, 0]) # 取出当前位置加上 look_back 的数据,作为输出
return numpy.array(dataX), numpy.array(dataY) # 将列表转换为 numpy 数组,并返回
# 定义随机种子,以便重现结果
numpy.random.seed(7) # 设置 numpy 的随机种子为 7,保证每次运行的结果一致
# 加载数据
dataframe = read_csv('LSTM\\LSTM_Fly\\airline-passengers.csv', usecols=[1], engine='python') # 使用 pandas 的 read_csv 函数,读取 csv 文件中的第二列(乘客数量)数据,存储为 dataframe
dataset = dataframe.values # 将 dataframe 转换为 numpy 数组,存储为 dataset
dataset = dataset.astype('float32') # 将 dataset 的数据类型转换为 float32,便于后续处理
# 缩放数据
scaler = MinMaxScaler(feature_range=(0, 1)) # 创建一个最小最大缩放器,用于将数据缩放到 0 到 1 的范围
dataset = scaler.fit_transform(dataset) # 使用缩放器对 dataset 进行拟合和转换,得到缩放后的数据
# 分割2/3数据作为测试
train_size = int(len(dataset) * 0.67) # 计算训练集的大小,为数据集长度的 2/3,取整数
test_size = len(dataset) - train_size # 计算测试集的大小,为数据集长度减去训练集大小
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] # 将数据集分割为训练集和测试集,前 train_size 个数据为训练集,后 test_size 个数据为测试集
# 预测数据步长为3,三个预测一个,3->1
look_back = 3 # 设置预测数据的步长为 3,即用三个数据预测一个数据
trainX, trainY = create_dataset(train, look_back) # 调用 create_dataset 函数,将训练集转换为监督学习的格式,得到训练集的输入和输出
testX, testY = create_dataset(test, look_back) # 调用 create_dataset 函数,将测试集转换为监督学习的格式,得到测试集的输入和输出
# 重构输入数据格式 [samples, time steps, features] = [93,1,3]
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1])) # 将训练集的输入数据重塑为 [样本数,时间步长,特征数] 的格式,即 [93,1,3],便于 LSTM 层的输入
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1])) # 将测试集的输入数据重塑为 [样本数,时间步长,特征数] 的格式,即 [47,1,3],便于 LSTM 层的输入
# 构建 LSTM 网络
model = Sequential() # 创建一个顺序模型,用于堆叠神经网络层
# 输入形状为 (1, 3) 表示每个样本只有一个时间步长,每个时间步长有 3 个特征
model.add(LSTM(4, input_shape=(1, look_back))) # 添加一个 LSTM 层,设置神经元个数为 4,输入形状为 (1, look_back),即 (1, 3)
model.add(Dense(1)) # 添加一个全连接层,设置神经元个数为 1,用于输出预测值
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型,设置损失函数为均方误差,优化器为 adam
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2) # 训练模型,设置迭代次数为 100,批次大小为 1,显示训练过程
# 对训练数据的Y进行预测
trainPredict = model.predict(trainX) # 使用模型对训练集的输入数据进行预测,得到训练集的预测值
# 对测试数据的Y进行预测
testPredict = model.predict(testX) # 使用模型对测试集的输入数据进行预测,得到测试集的预测值
# 对数据进行逆缩放
trainPredict = scaler.inverse_transform(trainPredict) # 使用缩放器对训练集的预测值进行逆转换,得到原始数据范围的预测值
trainY = scaler.inverse_transform([trainY]) # 使用缩放器对训练集的输出数据进行逆转换,得到原始数据范围的真实值
testPredict = scaler.inverse_transform(testPredict) # 使用缩放器对测试集的预测值进行逆转换,得到原始数据范围的预测值
testY = scaler.inverse_transform([testY]) # 使用缩放器对测试集的输出数据进行逆转换,得到原始数据范围的真实值
# 计算训练集和测试集的均方根误差(RMSE)
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0])) # 使用 math 库的 sqrt 函数,计算训练集的真实值和预测值的均方误差的平方根,存储为 trainScore
print('Train Score: %.2f RMSE' % (trainScore)) # 打印训练集的 RMSE,保留两位小数
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0])) # 使用 math 库的 sqrt 函数,计算测试集的真实值和预测值的均方误差的平方根,存储为 testScore
print('Test Score: %.2f RMSE' % (testScore)) # 打印测试集的 RMSE,保留两位小数
# 创建两个空数组,用于绘制训练集和测试集的预测值
trainPredictPlot = numpy.empty_like(dataset) # 使用 numpy 库的 empty_like 函数,创建一个和 dataset 形状相同的空数组,存储为 trainPredictPlot
trainPredictPlot[:, :] = numpy.nan # 将 trainPredictPlot 中的所有元素赋值为 numpy.nan,表示空值
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict # 将 trainPredict 中的预测值填充到 trainPredictPlot 中的相应位置,从 look_back 到 len(trainPredict)+look_back
testPredictPlot = numpy.empty_like(dataset) # 使用 numpy 库的 empty_like 函数,创建一个和 dataset 形状相同的空数组,存储为 testPredictPlot
testPredictPlot[:, :] = numpy.nan # 将 testPredictPlot 中的所有元素赋值为 numpy.nan,表示空值
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict # 将 testPredict 中的预测值填充到 testPredictPlot 中的相应位置,从 len(trainPredict)+(look_back*2)+1 到 len(dataset)-1
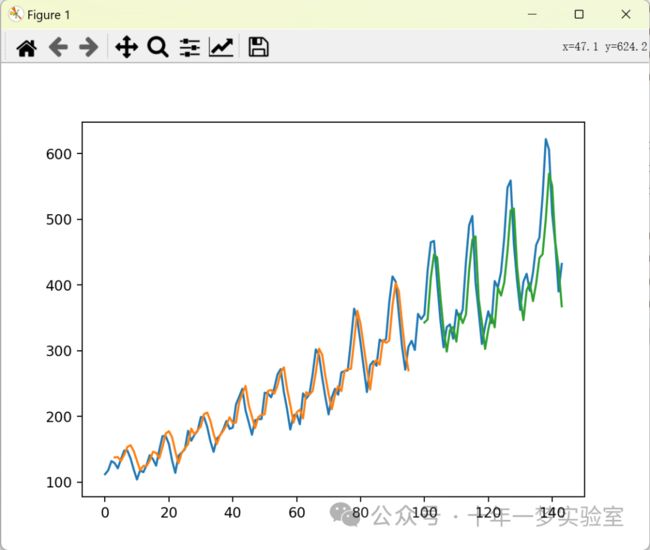
# 画图
plt.plot(scaler.inverse_transform(dataset)) # 使用 matplotlib 库的 plot 函数,绘制原始数据集的折线图,使用 scaler 的 inverse_transform 函数,将数据转换回原始范围
plt.plot(trainPredictPlot) # 使用 matplotlib 库的 plot 函数,绘制训练集的预测值的折线图
plt.plot(testPredictPlot) # 使用 matplotlib 库的 plot 函数,绘制测试集的预测值的折线图
plt.show() # 使用 matplotlib 库的 show 函数,显示图运行输出:
Epoch 97/100
93/93 - 0s - loss: 0.0017 - 228ms/epoch - 2ms/step
Epoch 98/100
93/93 - 0s - loss: 0.0017 - 223ms/epoch - 2ms/step
Epoch 99/100
93/93 - 0s - loss: 0.0017 - 229ms/epoch - 2ms/step
Epoch 100/100
93/93 - 0s - loss: 0.0017 - 234ms/epoch - 3ms/step
Train Score: 21.91 RMSE
Test Score: 63.09 RMSE3. 时间步长型回归 3个时间步长 1个特征 预测一个数据
在使用LSTM进行回归任务时,如何处理具有时间步长(time steps)的数据。
首先,在为LSTM网络准备数据时,包括了时间步长的概念。对于一些序列问题,每个样本可能具有不同数量的时间步长。例如,你可能有一台物理机器的测量数据,记录了故障或突增发生之前的情况。每个事件都可以被看作是一组观察值的样本,这些观察值构成了导致事件发生的时间步长,而观察到的变量则是特征。
时间步长为解决时间序列问题提供了另一种表述方式。与之前的窗口示例类似,你可以将过去的时间步长作为输入,用于预测下一个时间步长的输出。
与将过去的观察作为单独的输入特征不同,可以将它们视为一个输入特征的时间步长,这实际上更准确地描述了问题。
在代码示例中,通过与之前基于窗口的示例相同的数据表示方式,对数据进行重新整形,将列设置为时间步长维度,并将特征维度更改回1。例如:
# 重新整形输入为 [样本数, 时间步长, 特征数]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))最后,完整的代码清单以供参考。这段代码用于演示如何使用LSTM进行时间序列回归,其中数据的表示考虑了时间步长的概念。
# LSTM 用于国际航空旅客问题的时间步回归框架
import numpy # 导入 numpy 库,用于数组和矩阵运算
import matplotlib.pyplot as plt # 导入 matplotlib 库,用于绘图和可视化
from pandas import read_csv # 导入 pandas 库,用于读取和处理 csv 文件
import math # 导入 math 库,用于数学计算
from keras.models import Sequential # 导入 keras 库,用于构建和训练神经网络
from keras.layers import Dense # 导入 Dense 层,用于构建全连接层
from keras.layers import LSTM # 导入 LSTM 层,用于构建长短期记忆网络
from sklearn.preprocessing import MinMaxScaler # 导入 MinMaxScaler 类,用于将数据缩放到 0 到 1 的范围
from sklearn.metrics import mean_squared_error # 导入 mean_squared_error 函数,用于计算均方误差
import pandas as pd # 重新导入 pandas 库,并简写为 pd
pd.set_option('display.max_columns',1000) # 设置 pandas 的显示选项,最大列数为 1000
pd.set_option('display.width', 1000) # 设置 pandas 的显示选项,宽度为 1000
pd.set_option('display.max_colwidth',1000) # 设置 pandas 的显示选项,最大列宽为 1000
"""
数据形状:
x -> y = [93,3,1] -> [93,1]
x = [[[x1],[x2],[x3]] ,
[[x1],[x2],[x3]] ,
... ]
y = [[y1],
[y2],
[y3],
... ]
输入形状:
input_shape=(3,1)
代码差异:
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))
model.add(LSTM(4, input_shape=(look_back, 1)))。
"""
# 定义一个函数,将数据转换为监督学习的格式,即每 3 个数据作为输入,下一个数据作为输出
def create_dataset(dataset, look_back=1):
dataX, dataY = [], [] # 初始化两个空列表,用于存储输入和输出
for i in range(len(dataset)-look_back-1): # 遍历数据集,从第 0 个到倒数第 look_back+1 个
a = dataset[i:(i+look_back), 0] # 取出第 i 个到第 i+look_back-1 个数据,作为输入
dataX.append(a) # 将输入添加到 dataX 列表中
dataY.append(dataset[i + look_back, 0]) # 取出第 i+look_back 个数据,作为输出
return numpy.array(dataX), numpy.array(dataY) # 将列表转换为 numpy 数组,并返回
numpy.random.seed(7) # 设置 numpy 的随机种子,保证每次运行结果一致
dataframe = read_csv('LSTM\\LSTM_Fly\\airline-passengers.csv', usecols=[1], engine='python') # 读取 csv 文件,只使用第一列,即旅客数
dataset = dataframe.values # 将数据框转换为 numpy 数组
dataset = dataset.astype('float32') # 将数据类型转换为浮点数
scaler = MinMaxScaler(feature_range=(0, 1)) # 创建一个数据缩放器,将数据缩放到 0 到 1 的范围
dataset = scaler.fit_transform(dataset) # 对数据集进行缩放
train_size = int(len(dataset) * 0.67) # 计算训练集的大小,为数据集的 2/3
test_size = len(dataset) - train_size # 计算测试集的大小,为数据集的 1/3
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] # 将数据集分割为训练集和测试集
# 预测数据步长为3,三个预测一个,3->1
look_back = 3 # 设置预测数据步长为 3,即使用三个月的旅客数预测下一个月的旅客数
trainX, trainY = create_dataset(train, look_back) # 使用 create_dataset 函数将训练集转换为监督学习格式
testX, testY = create_dataset(test, look_back) # 使用 create_dataset 函数将测试集转换为监督学习格式
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1)) # 将训练集输入重构为 [samples, time steps, features] 的形状,即 [93,3,1]
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1)) # 将测试集输入重构为 [samples, time steps, features] 的形状,即 [44,3,1]
# 构建 LSTM 网络
model = Sequential() # 创建一个顺序模型
model.add(LSTM(4, input_shape=(look_back,1))) # 添加一个 LSTM 层,有四个神经元,输入形状为 (3,1)
model.add(Dense(1)) # 添加一个全连接层,有一个神经元,用于输出预测值
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型,使用均方误差作为损失函数,使用 Adam 作为优化器
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2) # 训练模型,使用 100 个周期,每个批次一个样本,打印训练过程
trainPredict = model.predict(trainX) # 对训练集的 Y 进行预测
testPredict = model.predict(testX) # 对测试集的 Y 进行预测
trainPredict = scaler.inverse_transform(trainPredict) # 将训练集预测结果逆缩放回原始范围
trainY = scaler.inverse_transform([trainY]) # 将训练集真实值逆缩放回原始范围
testPredict = scaler.inverse_transform(testPredict) # 将测试集预测结果逆缩放回原始范围
testY = scaler.inverse_transform([testY]) # 将测试集真实值逆缩放回原始范围
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0])) # 计算训练集的 RMSE 误差
print('Train Score: %.2f RMSE' % (trainScore)) # 打印训练集的 RMSE 误差
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0])) # 计算测试集的 RMSE 误差
print('Test Score: %.2f RMSE' % (testScore)) # 打印测试集的 RMSE 误差
trainPredictPlot = numpy.empty_like(dataset) # 创建一个和数据集形状相同的空数组,用于绘制训练集的预测值
trainPredictPlot[:, :] = numpy.nan # 将数组的所有元素设置为 nan,表示空值
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict # 将训练集的预测值填充到数组的相应位置,注意要留出 look_back 的空间
testPredictPlot = numpy.empty_like(dataset) # 创建一个和数据集形状相同的空数组,用于绘制测试集的预测值
testPredictPlot[:, :] = numpy.nan # 将数组的所有元素设置为 nan,表示空值
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict # 将测试集的预测值填充到数组的相应位置,注意要留出 look_back 的空间和最后一个空值
# 画图
plt.plot(scaler.inverse_transform(dataset)) # 绘制原始数据集的曲线,将缩放后的数据转换回原始范围
plt.plot(trainPredictPlot) # 绘制训练集的预测值的曲线
plt.plot(testPredictPlot) # 绘制测试集的预测值的曲线
plt.show() # 显示图像
testPredictPlot = numpy.empty_like(dataset) # 创建一个和数据集形状相同的空数组,用于绘制测试集的预测值
testPredictPlot[:, :] = numpy.nan # 将数组的所有元素设置为 nan,表示空值
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict # 将测试集的预测值填充到数组的相应位置,注意要留出 look_back 的空间和最后一个空值
# 画图
plt.plot(scaler.inverse_transform(dataset)) # 绘制原始数据集的曲线,将缩放后的数据转换回原始范围
plt.plot(trainPredictPlot) # 绘制训练集的预测值的曲线
plt.plot(testPredictPlot) # 绘制测试集的预测值的曲线
plt.show() # 显示图像运行输出:
Epoch 96/100
93/93 - 0s - loss: 0.0021 - 261ms/epoch - 3ms/step
Epoch 97/100
93/93 - 0s - loss: 0.0021 - 297ms/epoch - 3ms/step
Epoch 98/100
93/93 - 0s - loss: 0.0021 - 247ms/epoch - 3ms/step
Epoch 99/100
93/93 - 0s - loss: 0.0021 - 256ms/epoch - 3ms/step
Epoch 100/100
93/93 - 0s - loss: 0.0021 - 260ms/epoch - 3ms/step
Train Score: 22.91 RMSE
Test Score: 49.07 RMSE4. 批次间具有记忆功能的 LSTM
在Keras中如何使用“Memory Between Batches”来控制LSTM网络的内部状态。通常情况下,在每次训练批次(batch)结束、调用model.predict()或model.evaluate()时,LSTM网络的状态都会被重置。然而,通过在Keras中将LSTM层设置为“stateful”(有状态的),可以更精细地控制内部状态的清除。
具体而言,通过设置LSTM层的“stateful”参数,可以使其在整个训练序列上建立状态,并在需要时保持该状态以进行预测。为了实现这一点,有几个关键步骤:
不打乱训练数据: 在拟合网络时,训练数据不能被打乱。
手动重置网络状态: 在每次暴露于训练数据(一个epoch)后,需要通过调用
model.reset_states()来显式地重置网络状态。设置LSTM层为stateful: 在构建LSTM层时,需要将stateful参数设置为True。此外,不再指定输入维度,而是通过设置
batch_input_shape参数来硬编码批次中的样本数、样本中的时间步数以及时间步中的特征数。
示例代码如下:
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
model.reset_states()在这个例子中,通过循环进行训练,每个epoch结束后手动重置网络状态。在构建LSTM层时,指定了batch_input_shape和stateful参数。
model.add(LSTM(4, batch_input_shape=(batch_size, time_steps, features), stateful=True))最后,进行模型评估和预测时,需要使用相同的批次大小:
model.predict(trainX, batch_size=batch_size)这样就实现了LSTM网络在训练序列之间保持记忆状态的控制。完整代码:
# 使用 LSTM 模型预测国际航空旅客数量的问题,考虑到模型的记忆能力
import numpy # 导入 numpy 库,用于处理多维数组和矩阵运算
import matplotlib.pyplot as plt # 导入 matplotlib 库,用于绘制图形和可视化数据
from pandas import read_csv # 导入 pandas 库,用于读取和处理 CSV 文件
import math # 导入 math 库,用于进行数学计算
from keras.models import Sequential # 导入 keras 库,用于构建和训练深度学习模型
from keras.layers import Dense # 导入 keras 库中的 Dense 层,用于实现全连接层
from keras.layers import LSTM # 导入 keras 库中的 LSTM 层,用于实现长短期记忆网络
from sklearn.preprocessing import MinMaxScaler # 导入 sklearn 库中的 MinMaxScaler 类,用于将数据缩放到 0 到 1 的范围
from sklearn.metrics import mean_squared_error # 导入 sklearn 库中的 mean_squared_error 函数,用于计算均方误差
"""
之前是网络训练100个周期
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
每次网络训练1个周期,循环执行100次,每次循环重置网络状态
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
model.reset_states()
model.add(LSTM(4, batch_input_shape=(batch_size, time_steps, features), stateful=True))
model.
"""
# 定义一个函数,用于将数据集转换为有监督学习的格式,即给定输入序列,预测下一个值
# 参数 dataset 是一个二维数组,表示数据集
# 参数 look_back 是一个整数,表示输入序列的长度
# 返回值是两个二维数组,分别表示输入数据和输出数据
def create_dataset(dataset, look_back=1):
dataX, dataY = [], [] # 初始化两个空列表,用于存储输入数据和输出数据
for i in range(len(dataset)-look_back-1): # 遍历数据集中的每个元素,除了最后 look_back + 1 个
a = dataset[i:(i+look_back), 0] # 取出当前位置开始的 look_back 个元素,作为输入序列
dataX.append(a) # 将输入序列添加到输入数据列表中
dataY.append(dataset[i + look_back, 0]) # 取出当前位置后的第一个元素,作为输出值
return numpy.array(dataX), numpy.array(dataY) # 将输入数据和输出数据列表转换为 numpy 数组,并返回
numpy.random.seed(7) # 设置随机数种子,保证每次运行的结果一致
dataframe = read_csv('LSTM\\LSTM_Fly\\airline-passengers.csv', usecols=[1], engine='python') # 读取 CSV 文件中的第二列数据,即航空旅客数量
dataset = dataframe.values # 将数据框转换为二维数组
dataset = dataset.astype('float32') # 将数据类型转换为浮点数
scaler = MinMaxScaler(feature_range=(0, 1)) # 创建一个 MinMaxScaler 对象,用于将数据缩放到 0 到 1 的范围
dataset = scaler.fit_transform(dataset) # 对数据集进行缩放,并返回缩放后的数据集
train_size = int(len(dataset) * 0.67) # 计算训练集的大小,为数据集长度的 67%
test_size = len(dataset) - train_size # 计算测试集的大小,为数据集长度减去训练集的大小
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] # 将数据集划分为训练集和测试集,前 67% 为训练集,后 33% 为测试集
look_back = 3 # 设置输入序列的长度为 3,即用前 3 个值来预测下一个值
trainX, trainY = create_dataset(train, look_back) # 调用 create_dataset 函数,将训练集转换为有监督学习的格式,得到训练输入和训练输出
testX, testY = create_dataset(test, look_back) # 调用 create_dataset 函数,将测试集转换为有监督学习的格式,得到测试输入和测试输出
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1)) # 将训练输入的形状转换为 (样本数, 时间步数, 特征数),即 (96, 3, 1)
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1)) # 将测试输入的形状转换为 (样本数, 时间步数, 特征数),即 (44, 3, 1)
batch_size = 1 # 设置批处理的大小为 1,即每次训练或预测一个样本
model = Sequential() # 创建一个 Sequential 对象,用于构建一个顺序模型
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True)) # 向模型中添加一个 LSTM 层,设置神经元的个数为 4,输入的形状为 (批处理大小, 时间步数, 特征数),即 (1, 3, 1),并设置 stateful 参数为 True,表示保留上一批次的状态
model.add(Dense(1)) # 向模型中添加一个 Dense 层,设置输出的维度为 1,即预测值
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型,设置损失函数为均方误差,优化器为 adam
for i in range(100): # 迭代 100 次
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False) # 用训练输入和训练输出拟合模型,设置每次迭代的轮数为 1,批处理大小为 1,显示训练过程,不打乱数据顺序
model.reset_states() # 重置模型的状态,以便下一次迭代
trainPredict = model.predict(trainX, batch_size=batch_size) # 用训练输入预测训练输出,设置批处理大小为 1
model.reset_states() # 重置模型的状态,以便预测测试输出
testPredict = model.predict(testX, batch_size=batch_size) # 用测试输入预测测试输出,设置批处理大小为 1
trainPredict = scaler.inverse_transform(trainPredict) # 将训练预测值从 0 到 1 的范围还原为原始范围
trainY = scaler.inverse_transform([trainY]) # 将训练真实值从 0 到 1 的范围还原为原始范围
testPredict = scaler.inverse_transform(testPredict) # 将测试预测值从 0 到 1 的范围还原为原始范围
testY = scaler.inverse_transform([testY]) # 将测试真实值从 0 到 1 的范围还原为原始范围
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0])) # 计算训练集的均方根误差
print('Train Score: %.2f RMSE' % (trainScore)) # 打印训练集的均方根误差
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0])) # 计算测试集的均方根误差
print('Test Score: %.2f RMSE' % (testScore)) # 打印测试集的均方根误差
trainPredictPlot = numpy.empty_like(dataset) # 创建一个和数据集形状相同的空数组,用于绘制训练预测值
trainPredictPlot[:, :] = numpy.nan # 将数组中的所有元素设置为 nan,表示空值
# 将训练集预测的Y添加进数组,从第3位到第93+3位,共93行
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
testPredictPlot = numpy.empty_like(dataset) # 创建一个和数据集形状相同的空数组,用于绘制测试预测值
testPredictPlot[:, :] = numpy.nan # 将数组中的所有元素设置为 nan,表示空值
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict # 将测试预测值填充到数组中的相应位置
# 绘制原始数据,训练预测值和测试预测值的折线图,并显示
plt.plot(scaler.inverse_transform(dataset)) # 绘制原始数据的折线图,使用 scaler 对象将数据还原为原始范围
plt.plot(trainPredictPlot) # 绘制训练预测值的折线图
plt.plot(testPredictPlot) # 绘制测试预测值的折线图
plt.show() # 显示图形运行输出:
……
93/93 - 0s - loss: 0.0022 - 323ms/epoch - 3ms/step
93/93 - 0s - loss: 0.0022 - 291ms/epoch - 3ms/step
93/93 - 0s - loss: 0.0022 - 285ms/epoch - 3ms/step
93/93 - 0s - loss: 0.0022 - 270ms/epoch - 3ms/step
93/93 - 0s - loss: 0.0022 - 325ms/epoch - 3ms/step
Train Score: 24.88 RMSE
Test Score: 51.26 RMSE5. 带批次间记忆的堆叠LSTM
最后,让我们看一看LSTM的一个重大优势:它们能够在深度网络结构中成功训练的事实。
在Keras中,LSTM网络可以像堆叠其他类型的层一样进行堆叠。在配置时,需要添加一项配置,即在每个后续的LSTM层之前的LSTM层必须返回整个序列。可以通过将该层的return_sequences参数设置为True来实现。
您可以在前一节的状态化LSTM的基础上扩展为具有两个层,如下所示:
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True))
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))为了保持完整性,下面提供了完整的代码清单。
# Stacked LSTM for international airline passengers problem with memory
# 使用堆叠 LSTM 网络来解决国际航班乘客问题,考虑网络的记忆效果
import numpy # 导入 numpy 库,用于数组和矩阵运算
import matplotlib.pyplot as plt # 导入 matplotlib 库,用于绘图
from pandas import read_csv # 导入 pandas 库,用于读取 csv 文件
import math # 导入 math 库,用于数学计算
from keras.models import Sequential # 导入 keras 库,用于构建神经网络模型
from keras.layers import Dense # 导入 keras 库,用于添加全连接层
from keras.layers import LSTM # 导入 keras 库,用于添加 LSTM 层
from sklearn.preprocessing import MinMaxScaler # 导入 sklearn 库,用于数据缩放
from sklearn.metrics import mean_squared_error # 导入 sklearn 库,用于计算均方误差
# 将数据截取成3个一组的监督学习格式
# 定义一个函数,将数据集转换为监督学习的格式,即每三个数据作为输入,下一个数据作为输出
def create_dataset(dataset, look_back=1):
dataX, dataY = [], [] # 初始化输入和输出的空列表
for i in range(len(dataset)-look_back-1): # 遍历数据集,从第一个元素到倒数第四个元素
a = dataset[i:(i+look_back), 0] # 取出当前元素和后两个元素,作为输入的一部分
dataX.append(a) # 将输入添加到 dataX 列表中
dataY.append(dataset[i + look_back, 0]) # 取出当前元素后的第三个元素,作为输出的一部分
return numpy.array(dataX), numpy.array(dataY) # 将列表转换为 numpy 数组,并返回
# 定义随机种子,以便重现结果
# 设置随机数种子为 7,保证每次运行的结果一致
numpy.random.seed(7)
# 加载数据
# 使用 pandas 库的 read_csv 函数,读取 csv 文件中的数据,只使用第二列(乘客数量)
dataframe = read_csv('LSTM\\LSTM_Fly\\airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values # 将数据转换为 numpy 数组
dataset = dataset.astype('float32') # 将数据类型转换为浮点数
# 缩放数据
# 使用 sklearn 库的 MinMaxScaler 函数,将数据缩放到 0 到 1 的范围
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# 分割2/3数据作为测试
# 将数据集分割为训练集和测试集,训练集占 2/3,测试集占 1/3
train_size = int(len(dataset) * 0.67) # 计算训练集的大小,为数据集长度的 2/3,取整数
test_size = len(dataset) - train_size # 计算测试集的大小,为数据集长度减去训练集的大小
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] # 将数据集按照训练集和测试集的大小分割
# 预测数据步长为3,三个预测一个,3->1
# 设置预测数据的步长为 3,即每三个数据作为输入,下一个数据作为输出,3->1
look_back = 3
trainX, trainY = create_dataset(train, look_back) # 将训练集转换为监督学习的格式,得到输入和输出
testX, testY = create_dataset(test, look_back) # 将测试集转换为监督学习的格式,得到输入和输出
# 重构输入数据格式 [samples, time steps, features] = [93,3,1]
# 将输入数据的形状重构为 [样本数,时间步长,特征数],即 [93,3,1],符合 LSTM 层的输入要求
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1)) # 将训练集输入重构为 [93,3,1]
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1)) # 将测试集输入重构为 [44,3,1]
# 构建 LSTM 网络
# 设置批处理大小为 1,即每次输入一个样本
batch_size = 1
model = Sequential() # 创建一个顺序模型
# 堆叠两层 LSTM 网络,参数 return_sequences=True 表示将上层的输入形状向下继续传递
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True)) # 添加第一层 LSTM 层,设置神经元个数为 4,输入形状为 (1,3,1),保持网络状态,向下传递输入形状
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True)) # 添加第二层 LSTM 层,设置神经元个数为 4,输入形状为 (1,3,1),保持网络状态
model.add(Dense(1)) # 添加一个全连接层,设置输出神经元个数为 1
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型,设置损失函数为均方误差,优化器为 adam
# 网络训练一个周期,循环训练100次
# 使用 for 循环,将模型训练 100 次,每次训练一个周期
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False) # 使用 fit 函数,将训练集输入和输出作为参数,设置周期数为 1,批处理大小为 1,显示训练过程,不打乱数据顺序
# 每次训练完都重置网络状态
model.reset_states() # 使用 reset_states 函数,重置网络状态,避免上一次训练的影响
# 对训练数据的Y进行预测
# 使用 predict 函数,将训练集输入作为参数,得到训练集的预测输出
trainPredict = model.predict(trainX, batch_size=batch_size)
# 重置网络状态
# 使用 reset_states 函数,重置网络状态,避免上一次预测的影响
model.reset_states()
# 对测试数据的Y进行预测
# 使用 predict 函数,将测试集输入作为参数,得到测试集的预测输出
testPredict = model.predict(testX, batch_size=batch_size)
# 对数据进行逆缩放
# 使用 scaler.inverse_transform 函数,将预测输出和真实输出逆缩放,还原为原始数据的范围
trainPredict = scaler.inverse_transform(trainPredict) # 将训练集预测输出逆缩放
trainY = scaler.inverse_transform([trainY]) # 将训练集真实输出逆缩放
testPredict = scaler.inverse_transform(testPredict) # 将测试集预测输出逆缩放
testY = scaler.inverse_transform([testY]) # 将测试集真实输出逆缩放
# 计算RMSE误差
# 使用math库的sqrt函数,计算训练集和测试集的预测值和真实值之间的均方根误差(RMSE),并存储为trainScore和testScore变量
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
# 打印RMSE误差
# 使用print函数,输出训练集和测试集的RMSE误差,保留两位小数
print('Train Score: %.2f RMSE' % (trainScore))
print('Test Score: %.2f RMSE' % (testScore))
# 构造一个和dataset格式相同的数组,共145行,dataset为总数据集,把预测的93行训练数据存进去
# 使用numpy库的empty_like函数,创建一个和dataset数组形状相同的空数组,用于存储训练集的预测值,命名为trainPredictPlot
trainPredictPlot = numpy.empty_like(dataset)
# 使用numpy库的nan值,填充trainPredictPlot数组,使其所有元素都为nan
trainPredictPlot[:, :] = numpy.nan
# 将训练集的预测值trainPredict数组,添加到trainPredictPlot数组中,从第look_back位开始,到第len(trainPredict)+look_back位结束,共len(trainPredict)行
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# 构造一个和dataset格式相同的数组,共145行,把预测的后44行测试数据数据放进去
# 使用numpy库的empty_like函数,创建一个和dataset数组形状相同的空数组,用于存储测试集的预测值,命名为testPredictPlot
testPredictPlot = numpy.empty_like(dataset)
# 使用numpy库的nan值,填充testPredictPlot数组,使其所有元素都为nan
testPredictPlot[:, :] = numpy.nan
# 将测试集的预测值testPredict数组,添加到testPredictPlot数组中,从第len(trainPredict)+(look_back*2)+1位开始,到第len(dataset)-1位结束,共len(testPredict)行
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
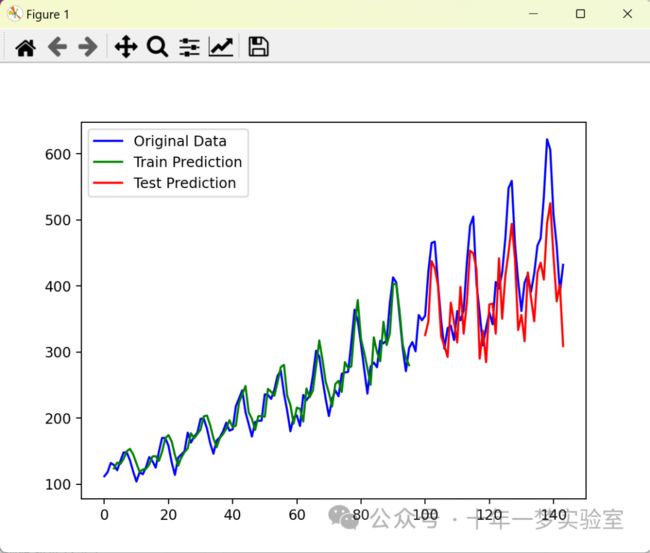
# 画图
# 使用matplotlib库的pyplot模块,绘制图形
# 使用plt.plot函数,绘制原始数据集dataset的曲线,颜色为蓝色,标签为'Original Data'
plt.plot(scaler.inverse_transform(dataset), color='blue', label='Original Data')
# 使用plt.plot函数,绘制训练集预测值trainPredictPlot的曲线,颜色为绿色,标签为'Train Prediction'
plt.plot(trainPredictPlot, color='green', label='Train Prediction')
# 使用plt.plot函数,绘制测试集预测值testPredictPlot的曲线,颜色为红色,标签为'Test Prediction'
plt.plot(testPredictPlot, color='red', label='Test Prediction')
# 使用plt.legend函数,显示图例
plt.legend()
# 使用plt.show函数,显示图形
plt.show()运行输出:
……
93/93 - 0s - loss: 0.0017 - 422ms/epoch - 5ms/step
93/93 - 0s - loss: 0.0017 - 412ms/epoch - 4ms/step
93/93 - 0s - loss: 0.0017 - 450ms/epoch - 5ms/step
93/93 - 0s - loss: 0.0017 - 414ms/epoch - 4ms/step
93/93 - 0s - loss: 0.0017 - 411ms/epoch - 4ms/step
93/93 - 0s - loss: 0.0017 - 420ms/epoch - 5ms/step
93/93 - 0s - loss: 0.0017 - 426ms/epoch - 5ms/step
93/93 - 0s - loss: 0.0017 - 437ms/epoch - 5ms/step
93/93 - 0s - loss: 0.0017 - 412ms/epoch - 4ms/step
93/93 - 0s - loss: 0.0017 - 453ms/epoch - 5ms/step
Train Score: 20.86 RMSE
Test Score: 59.16 RMSE附-LSTM模型参数和调用说明:
LSTM 模型的参数:
units: LSTM 层的输出空间的维度,即 LSTM 单元的个数,也就是隐藏层的大小。这个参数决定了 LSTM 层的复杂度和表达能力,一般来说,越大越强,但也会增加计算量和过拟合的风险。
activation: LSTM 层的激活函数,用于计算单元状态(cell state)和输出门(output gate)的输出。默认为双曲正切函数(tanh),也可以选择其他的激活函数,如 ReLU,sigmoid 等。激活函数的作用是引入非线性,增强模型的拟合能力。
recurrent_activation: LSTM 层的循环激活函数,用于计算遗忘门(forget gate),输入门(input gate)和输出门(output gate)的激活值。默认为硬 S 型函数(hard_sigmoid),也可以选择其他的激活函数,如 sigmoid,ReLU 等。循环激活函数的作用是控制门的开关,调节信息的流动。
use_bias: 布尔值,表示是否使用偏置向量。偏置向量是神经网络中的一个常数项,可以增加模型的灵活性,改善拟合效果。
kernel_initializer: 权重矩阵的初始化器,用于输入的线性变换。权重矩阵是神经网络中的一个参数矩阵,用于将输入数据映射到隐藏层。初始化器是一种方法,用于给权重矩阵赋予初始值,影响模型的收敛速度和效果。
recurrent_initializer: 循环权重矩阵的初始化器,用于循环状态的线性变换。循环权重矩阵是神经网络中的一个参数矩阵,用于将上一时刻的隐藏层状态映射到当前时刻的隐藏层。初始化器的作用同上。
bias_initializer: 偏置向量的初始化器。偏置向量的作用同上。初始化器的作用同上。
unit_forget_bias: 布尔值,表示是否在初始化时给遗忘门的偏置向量加上 1。这样做的好处是让遗忘门更倾向于记住信息,而不是忘记信息。这是一种启发式的方法,有助于提高模型的性能。如果设置为 True,那么偏置向量的初始化器将被强制为零初始化器(zeros)。
kernel_regularizer: 权重矩阵的正则化函数。正则化函数是一种方法,用于给模型添加一些额外的约束,防止过拟合或欠拟合。常见的正则化函数有 L1,L2,dropout 等。
recurrent_regularizer: 循环权重矩阵的正则化函数。作用同上。
bias_regularizer: 偏置向量的正则化函数。作用同上。
activity_regularizer: 输出的正则化函数。作用同上,但是作用于 LSTM 层的输出,而不是参数。
kernel_constraint: 权重矩阵的约束函数。约束函数是一种方法,用于限制权重矩阵的取值范围,防止梯度爆炸或消失。常见的约束函数有 max_norm,min_max_norm,unit_norm 等。
recurrent_constraint: 循环权重矩阵的约束函数。作用同上。
bias_constraint: 偏置向量的约束函数。作用同上。
dropout: 0 到 1 之间的浮点数,表示输入的线性变换中丢弃的单元的比例。丢弃是一种正则化方法,用于随机关闭一些神经元,减少模型的复杂度,防止过拟合。
recurrent_dropout: 0 到 1 之间的浮点数,表示循环状态的线性变换中丢弃的单元的比例。作用同上,但是作用于循环状态,而不是输入。
return_sequences: 布尔值,表示是否返回输出序列中的最后一个输出,或者完整的序列。如果为 True,那么 LSTM 层的输出将是一个三维张量,形状为 (batch_size, timesteps, units);如果为 False,那么 LSTM 层的输出将是一个二维张量,形状为 (batch_size, units)。这个参数决定了 LSTM 层的输出能否作为另一个 LSTM 层的输入。
return_state: 布尔值,表示是否除了输出之外,还返回最后一个状态。如果为 True,那么 LSTM 层的返回值将是一个列表,包含输出,最后一个隐藏状态和最后一个单元状态;如果为 False,那么 LSTM 层的返回值将只有输出。这个参数决定了 LSTM 层的状态能否作为另一个 LSTM 层的初始状态。
go_backwards: 布尔值,表示是否反向处理输入序列,并返回反向的序列。如果为 True,那么 LSTM 层将从最后一个时间步开始,逐步向前处理输入序列,并返回反向的输出序列;如果为 False,那么 LSTM 层将正常处理输入序列,并返回正向的输出序列。这个参数可以用于构建双向 LSTM(Bidirectional LSTM)。
stateful: 布尔值,表示是否保持批次之间的状态。如果为 True,那么 LSTM 层将在每个批次结束时,将最后一个状态作为下一个批次的初始状态;如果为 False,那么 LSTM 层将在每个批次开始时,重置状态为零。这个参数可以用于处理较长的序列,或者实现序列到序列的模型(Seq2Seq)。
unroll: 布尔值,表示是否展开循环。如果为 True,那么 LSTM 层将展开循环,使用静态计算图,提高计算效率,但是增加内存消耗;如果为 False,那么 LSTM 层将使用动态计算图,节省内存,但是降低计算效率。展开循环只适用于较短的序列,否则可能会导致内存溢出。
time_major: 布尔值,表示输入和输出张量的形状格式。如果为 True,那么输入和输出的形状将是 (timesteps, batch_size, ...),即时间步优先;如果为 False,那么输入和输出的形状将是 (batch_size, timesteps, ...),即批次优先。使用时间步优先的格式可以提高计算效率,因为它避免了在 RNN 计算的开始和结束时的转置操作。但是,大多数 TensorFlow 的数据都是批次优先的,所以默认情况下,这个函数接受批次优先的输入,并输出批次优先的输出。
LSTM 模型的调用参数:
inputs: 一个三维张量,表示输入序列,形状为 (batch_size, timesteps, input_dim) 或 (timesteps, batch_size, input_dim),取决于 time_major 参数的值。
mask: 一个二维的布尔张量,形状为 (samples, timesteps),表示是否对给定的时间步进行掩码。一个 True 的元素表示对应的时间步应该被使用,而一个 False 的元素表示对应的时间步应该被忽略。掩码的作用是让 LSTM 层能够处理不等长的序列,或者忽略一些无效的数据。
training: 一个 Python 布尔值,表示 LSTM 层应该在训练模式还是推理模式下运行。这个参数会传递给 LSTM 单元在调用时。这个参数只有在使用 dropout 或 recurrent_dropout 时才有意义。训练模式下,LSTM 层会随机丢弃一些单元,以防止过拟合;推理模式下,LSTM 层会使用所有的单元,以保持最佳的预测效果。
initial_state: 一个张量列表,表示传递给 LSTM 单元的第一次调用的初始状态。这个参数可以用于指定 LSTM 层的初始隐藏状态和初始单元状态,而不是使用零状态。这个参数可以用于实现序列到序列的模型(Seq2Seq),或者在多层 LSTM 之间传递状态。
参考网址:
https://machinelearningmastery.com/time-series-prediction-lstm-recurrent-neural-networks-python-keras/