数据结构与算法(九)图链式存储
邻接表
度:无向图的度:顶点与邻接点连接的边就做度。有向图的度:指向顶点的边叫做入度,由顶点指向其他邻接点的边叫做出度
顶点:存储自身顶点信息和指向下一个临界点的指针
邻接点:保存临接点的存储下标和下一个邻接点的指向指针
存储方式:单向链接
无向图存储
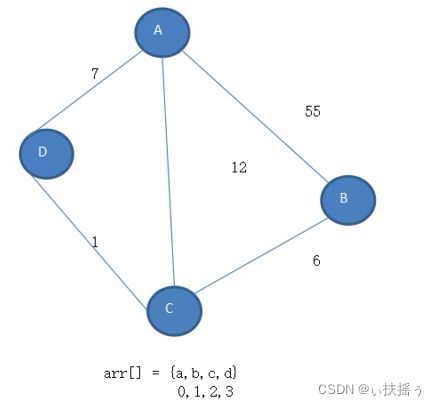
arr[] = {a, d, c, b} 0 1 2 3
一个节点可以能多个邻接点,该节点可通过索引进行选择下一个邻接点选择哪个,如下图:
头表和邻接表
由上图可知,A有三个邻接点,分别是B C D。B有两个邻接点,分别是A C
在需要时,A可以直接指向C或D
有向图存储
有向图中,每一条边都有方向指向,分为出边和入边
在邻接表存储中只有出边没有入边
如上,只有A到E的边,没有E到A的边
带权图,只需同上加一个 权值表即可
在实际存储过程中,顶点和邻接点常以两种形式存储
邻接点:
struct AjdNode
{
int index; 下标
struct AdjNode* next; 指向下一个同类型的指针
}
顶点:
struct Node
{
int data; 任意类型的数据域
struct AjdNode* first; 指向第一个邻接点结构的指针
}
邻接表代码实现
const int g_maxcount = 1000; 定义一个最大节点数
int g_edge;
int g_nCount;
typedef struct _Node 按常理应有顶点和邻接点结构体,但此处省略写,两者共用一个结构体
{
int nIndex; 既是邻接点下标也是data
struct _Node * next;
}Node;
Node* head[g_nMaxCount];
声明一个数组,head相当于顶点,[]中相当于下标指向某一个顶点
void Create() 创建
{
std::cout << "Input Node Count And Edge:" ;
char cStart;
char cEnd; 边的两头,两个节点的字符
std::cin >> g_nCount >> g_Edge; 输入要有多少个节点多少个边
for(size_t i = 0; i < g_nEdge; i++)
{
std::cin >> cStart >> cEnd; 输入边的两头 如边ab ac
int headIndex = cStart - 'a'; 转成数字编号,头节点的下标
int nEdgeIndex = cEnd - 'a'; 尾节点的下标 input a - a = 0, b - a = 1 ,ASCII码应用
Node* newNode = new Node; 进行插入
newNode->nIndex = nEdgeIndex;
比如head是a edge是b,输入ab,a是顶点,b是邻接点,以邻接点b即b-a的数值当作下标从a指向b,具体理解如下
newNode->next = head[nheadIndex];头插法,将新节点向下的指针,指向原有的第一个邻接点
head[nheadIndex] = newNode;
}
}
void print() 输出
{
for(size_t i = 0; i < g_nCount; i++) 判断有多少个头
{
for(Node* temp = head[i]; temp != NULL; temp = temp->next) 遍历所有的头的邻接点
临时节点指向头节点
{
std::out << "[" <
}
std::cout << std::endl;
}
}
链式前向星
链式前向星由边集数组和头顶点数组组成,优点是可以快速访问一个点所有邻接点
边集数组 egde[i] 存储边
#define max 100
struct node 边集数组结构
{
int to; 结尾的点
struct node * next;
int weight; 权值
}edge[max]; 定义有100个结构体
如下一个无向图
头节点数组
head[i] 存储下标 指向的第一个edge的下标
边集数组便是将上述两个图结合起来,具体如下
最左边一列表示以哪个节点作为顶点
head表示该顶点指向的第一个边,如上图第一行head为2表示A指向了第2个边即edge[2]
上图中存储了各个边的信息 如第一条边存储了AB边,B是1,to是1
如上图边集数组A指向C之后A指向B,则在上图AC边next指向AB边
链式前向星代码实现
const int g_MaxCount = 100;
int g_nCount; 节点
int g_nEdge; 边
int g_nIndex; 索引
int g_nTo; 尾节点
int g_nWeight; 权值
int g_nHead; 顶点
int head[g_MaxCount];
struct Edge 边集数组
{
int to;
int weight;
int next;
}e[g_MaxCount];
void init()
{
memset(head, -1, (sizeof(int) * g_MaxCount));
g_nHead = 0;
}
void add(int index; int to; int weight)
{
e[g_nHead].to = to;
e[g_nHead].weight = weight;
e[g_Head].next = head[index];
head[index] = g_nHead++;
}
void print()
{
for(size_t i = 1; i <= g_nCount; i++)
{
std::cout << i << ":\t";
for(size_t j = head[i]; ~j; j = e[j].next) 遍历头数组 ~j相当于j != -1
{
std::cout << "[" << e[i].to << e[i].weight << "]\t";
}
std::cout << std::endl;
}
}
应用:
std::cin >> g_nCount >> g_nEdge;
init();
for(size_t i = 1; i <= g_nEdge; i++)
{
std::cin >> g_nIndex >> g_nTo >> g_nWeight;
add(g_nIndex, g_nTo, g_nWeigh);
add(g_nTo, g_nIndex, g_nWeigh);
}
print();
应用结果如下图