卷积神经网络全过程
作为计算机视觉中最重要的部分卷积神经网络,从输入到输出做一个全方面的梳理。
卷积神经网络一般包含:
卷积神经网络一般包含:
-
- 卷积层
-
- 单层卷积网络
- 池化层
- 全连接层
卷积层
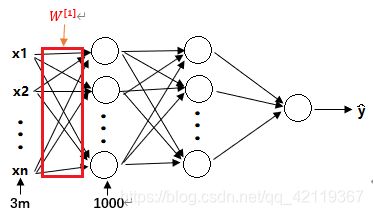
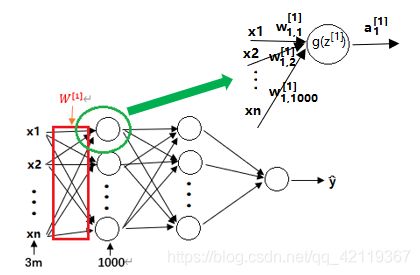
假设我们输入的图像大小为 64 * 64 的RGB小图片,数据量就是 64 * 64 * 3,计算得到数据量大小为 12288。如果输入为 1000*1000 的RGB图片,那么数据量将是300万(3m表示300万),也就是我们要输入的特征向量 x x x 的维度高达300万。如果在第一隐藏层中有1000个神经单元,该层的权值矩阵为 W [ 1 ] W^{[1]} W[1] ,
W [ 1 ] = [ w 1 , 1 [ 1 ] w 1 , 2 [ 1 ] . . . w 1 , 1000 [ 1 ] w 2 , 1 [ 1 ] w 2 , 2 [ 1 ] . . . w 2 , 1000 [ 1 ] ⋮ ⋮ ⋱ ⋮ w n , 1 [ 1 ] w n , 2 [ 1 ] . . . w n , 1000 [ 1 ] ] W^{[1]}=\begin{bmatrix} w_{1,1}^{[1]} & w_{1,2}^{[1]} & ... & w_{1,1000}^{[1]} \\ w_{2,1}^{[1]} & w_{2,2}^{[1]} & ... & w_{2,1000}^{[1]} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n,1}^{[1]} & w_{n,2}^{[1]} & ... & w_{n,1000}^{[1]} \end{bmatrix} W[1]=⎣⎢⎢⎢⎢⎡w1,1[1]w2,1[1]⋮wn,1[1]w1,2[1]w2,2[1]⋮wn,2[1]......⋱...w1,1000[1]w2,1000[1]⋮wn,1000[1]⎦⎥⎥⎥⎥⎤
这个矩阵的大小将会是 1000 * 300 万,数据量相当大。要处理包含30亿参数的神经网络,将需要极大的内存需求,为此,我们需要进行卷积计算,降低计算参数。
卷积操作运算过程:
假设我们输入了一个 5 * 5 的一张单通道的小图片,在卷积核 k e r n e l kernel kernel 的计算后(步长为1的情况下)数据由原来的 5 * 5 变成了 3 * 3的大小。
k e r n e l = [ 0 1 2 2 2 0 0 1 2 ] kernel=\begin{bmatrix} 0 & 1 & 2 \\ 2 & 2 & 0 \\ 0 & 1 & 2 \end{bmatrix} kernel=⎣⎡020121202⎦⎤
也可能是加入 p a d d i n g padding padding 的情况,如下:

卷积后的数据尺寸计算公式为:
out = n + 2 p − f s + 1 \dfrac{n+2p-f}{s}+1 sn+2p−f+1
- n n n:原始图像尺寸 n ∗ n n * n n∗n
- p p p:即 padding,原始图像边缘的填充像素列数
- f f f:即 f i l t e r filter filter 的 k e r n e l kernel kernel 尺寸,这里需要强调下,因为在此原始图像只有一个通道,所以这个卷积 f i l t e r filter filter 只用了一个 k e r n e l kernel kernel,后面不同的情况会再次说明。
- s s s:即 s t r i d e stride stride, f i l t e r filter filter 在图像上每次的移动步长。
再看下多层卷积,以RGB图像为例:

输入一个 6 * 6 * 3 的图像,说明:第一个6代表图像高度,第二个6代表宽度,3代表通道数, f i l t e r filter filter也要有相同的尺度。 f i l t e r filter filter (中文翻译:过滤器/滤波器)是3个 3 * 3 大小尺寸的 k e r n e l kernel kernel 组成,后面写成 3 * 3 * 3 ,最后的一个数字是通道数,为了简化该过滤器的图像,不再把它画成3个矩阵的堆叠,将它画成一个三维的立方体。
为了计算这个卷积操作的输出,将该过滤器放在最左上角的位置,这个 3 * 3 * 3的过滤器有27个数,一次取这27个数,然后乘以相对应的红绿蓝通道中的数字,然后把这些数相加,就会得到第一个数值。把这个立方体滑动到下一个单元,再做同样的操作,就得到下一个输出,以此类推。这个输出会是一个 4 * 4 的数据,注意是 4 * 4 * 1,这就是在该过滤器下的输出特征。

举例说明,如果你想检测图像红色通道的边缘,可以将第一个 k e r n e l kernel kernel设为 [ 1 0 − 1 1 0 − 1 1 0 − 1 ] \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \end{bmatrix} ⎣⎡111000−1−1−1⎦⎤,后面两个设为 [ 0 0 0 0 0 0 0 0 0 ] \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} ⎣⎡000000000⎦⎤,那么这就是一个检测垂直边缘的过滤器,但只对红色通道有效。如果三个通道都是 [ 1 0 − 1 1 0 − 1 1 0 − 1 ] \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \end{bmatrix} ⎣⎡111000−1−1−1⎦⎤,就变成了边缘检测器。
如果你想获得多个特征,那就需要多个过滤器了,如下图所示,在两个不同的 3 * 3 * 3 的过滤器下,得到了两个 4 * 4 的输出,堆叠在一起,便形成一个 4 * 4 * 2 的立方体。
单层卷积网络
已经通过两个过滤器卷积处理一个三维图像,并输出两个不同的 4 * 4 矩阵,最终各自形成一个卷积神经网络层,然后增加偏差(它是一个实数),通过Python广播机制给这16个元素都加上同一偏差。然后应用非线性激活函数,比如 ReLU,输出结果是一个 4 * 4 的矩阵。

以上过程便是前向传播,数学表达式即是:
z [ 1 ] = W [ 1 ] a [ 0 ] + b [ 1 ] z^{[1]}=W^{[1]}a^{[0]}+b^{[1]} z[1]=W[1]a[0]+b[1]
a [ 1 ] = g ( z [ 1 ] ) a^{[1]}=g(z^{[1]}) a[1]=g(z[1])
其中
- a [ 0 ] a^{[0]} a[0]代表 x x x,在这里就是 6 * 6 * 3 =108个输入元素
- g ( ) g() g() 代表激活函数
- a [ 1 ] a^{[1]} a[1] 是该层的输出
如下示意图:
示例中我们有两个过滤器,因此得到一个 4 * 4 * 2的输出,如果我们用了10个过滤器,就会得到 4 * 4 * 10 的输出,即10个特征,将他们堆叠在一起,也就是 a [ 1 ] a^{[1]} a[1]。
神经网络到底存储的是什么参数用来判别以后未知的输入数据呢?
现在我们假定有10个过滤器,该层中每个过滤器是 3 * 3 * 3 = 27个参数,又因为每个过滤器有 1 个偏置 b b b,加在一起是 ( 27 + 1 ) ∗ 10 = 280 (27+1)*10=280 (27+1)∗10=280参数,在该层神经网络存储的数据就是这280个参数。
不论输入图片多大,1000 * 1000也好,60 * 60也好,参数始终都是280个。即使这些图片很大,存储数据很少,这就是神经网络的一个特征,叫做“避免过拟合”。
池化层
该层不难理解:
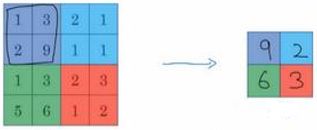
加入输入一个 4 * 4 矩阵,使用最大池化: k e r n e l kernel kernel=[2, 2], s t r i d e stride stride=2。执行过程:是将 4 * 4 的输入拆分成不同的区域,输出每个区域的最大元素值,便得到了一个 2 * 2 的矩阵。
再看一个 k e r n e l kernel kernel=[3, 3], s t r i d e stride stride=1的例子,采用最大池化:
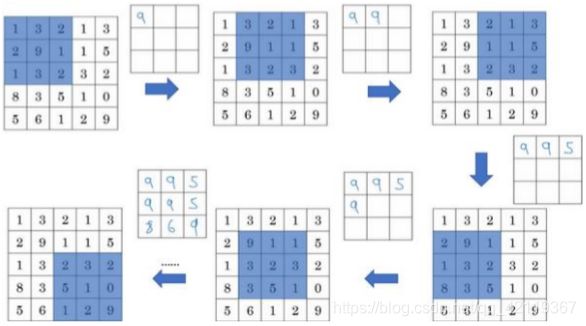
以上就是一个二维输入的最大池化演示,如果输入是三维的,那么输出也是三维的,例如:输入是 5 * 5 * 2,输出为 3 * 3 * 2。计算池化的方法就是分别对每个通道采用上述的计算过程。池化操作也可以边缘填充 p a d d i n g padding padding,
池化操作输出计算公式:
out = n + 2 p − f s + 1 \dfrac{n+2p-f}{s}+1 sn+2p−f+1
- n n n:原始图像尺寸 n ∗ n n * n n∗n
- p p p:即 padding,原始图像边缘的填充像素列数
- f f f:即 f i l t e r filter filter 的 k e r n e l kernel kernel 尺寸
- s s s:即 s t r i d e stride stride, f i l t e r filter filter 在图像上每次的移动步长
注意:池化过程中没有需要学习的参数,只需要调整手动设置的超参数。
参数和超参数区别
比如算法中的 l e a r n i n g learning learning r a t e rate rate(学习率), i t e r a t i o n s iterations iterations(梯度下降法循环的数量), L L L(隐藏层数目), n n n(隐藏层单元数目) 都需要你来设置,这些数字实际上控制了最后的参数 W W W、 b b b 的值,所以它们被称为超参数。
全连接层
加入输入一张 32 * 32 * 3 的图片,最后做手写体数字识别。
在此采用的网络模型和 LeNet-5 神经网络非常相似,许多参数选择都与 LeNet-5 相同。假设第一层使用过滤器 5 * 5, s s s=1, p a d d i n g padding padding=0(后续为0就不再写出),过滤器个数为6,那么输出为 28 * 28 * 6。将这层标记为 CONV1,增加了偏差,应用了非线性函数,选一个ReLU函数吧,最后输出 CONV1 的结果。
然后构建一个池化层,选择最大池化,参数 f f f=2, s s s=2。因此输出为 14 * 14 * 6,将该输出标记为 POOL1。
在文献中,卷积有两种分类,与划分存在一致性,一类卷积是一个卷积层和一个池化层作为一层,这就是神经网络中的 Layer1;另一类是把卷积层和池化层都单独作为一层。在计算神经网络时,通常只统计具有权重和参数的层,因为池化层没有权重和参数,只有一些超参数,所以才会有这样的标记处理。以上只是两种不同的标记术语。
再构建一个卷积层,过滤器为 5 * 5 , s s s=1,这次用16个过滤器,最后输出为 10 * 10 * 16 的矩阵,标记为 CONV2。
继续做最大池化, f f f=2, s s s=2,结果是 5 * 5 * 16 标记为 POOL2。
下面进入全连接的处理:
5 * 5 * 16 矩阵包含400个元素,现在将 POOL2 平整化为一个大小为400维的一维向量。我们可以把平整化结果想象成一个400的神经元集合,利用这400个单元构建下一层,下一层有120个单元,这就是我们的第一个全连接层,标记为 FC3。这个全连接层很像前面的单神经网络层,它的权重矩阵为 W [ 3 ] W^{[3]} W[3],维度为 120 * 400。
它的数学处理:
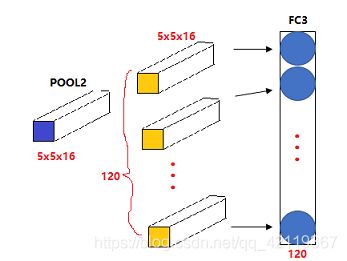
如上图所示,对于 5 * 5 * 16 的输入数据,我们创建和输入数据一样大小的过滤器: 5 * 5 * 16 ,可以理解为有 16 个 k e r n e l kernel kernel, k e r n e l kernel kernel尺寸为 5 * 5,通过一个这样的过滤器便可得到一个数值,采用120个这样的过滤器,就会得到120个数值,这样便得到了我们的全连接层的数据了。
然后对这个120个单元再添加一个全连接层,这层含有84个单元,标记为FC4,最后用这84个单元填充一个 softmax 单元。如果想通过手写数字来识别 0-9 这10个数字,这个 softmax 就会有10个输出。
最后来看下神经网络的激活值形状,激活值大小和参数数量。输入为 32 * 32 * 3=3072,所以激活值 a [ 0 ] a^{[0]} a[0] 有3072维,激活值矩阵维 32 * 32 * 3,输入层没有参数。看下该网络模型所有层的情况:
| Neural network | Activation Shape | Activation Size | parameters |
|---|---|---|---|
| Input | (32,32,3) | 3072 | 0 |
| CONV1 (f=5,s=1) | (28,28,6) | 4704 | 456 |
| POOL1 | (14,14,6) | 1176 | 0 |
| CONV2(f=5,s=1) | (10,10,16) | 1600 | 2416 |
| POOL2 | (5,5,16) | 400 | 0 |
| FC3 | (120,1) | 120 | 48001 |
| FC4 | (84,1) | 84 | 10081 |
| Softmax | (10,1) | 10 | 841 |
有几点要注意,池化层没有参数;第二卷积层的参数相对较少,其实许多参数都存在于神经网络的全连接层。观察可发现,随着神经网络的加深,激活值尺寸会逐渐变小,如果激活值尺寸下降太快,会影响神经网络性能。示例中,激活值尺寸在第一层为6000,然后减少为1600,再减少到84,最后输出softmax结果。许多神经网络都具有这些属性,模式上也相似。