vivado实现4x4阵列乘法器
vivado实现4*4阵列乘法器
- 阵列乘法器
-
- 阵列乘法器的原理
- 代码
- 模块lie1
- 模块lie234
- 模块超前进位加法器
- 超前进位模块
- 以及最后一个模块全加器
- 仿真文件
- 最后附上全部代码
阵列乘法器
经历了苦痛的在家网课,上课也没怎么认真听,后果就是要在做实验前恶补。orz这是我在做计组课程设计的东西。
阵列乘法器的原理
其实也没什么好说的,要是大家上过课的话应该也知道就是全加器和超前进位加法器构成的绝对值阵列乘法器。
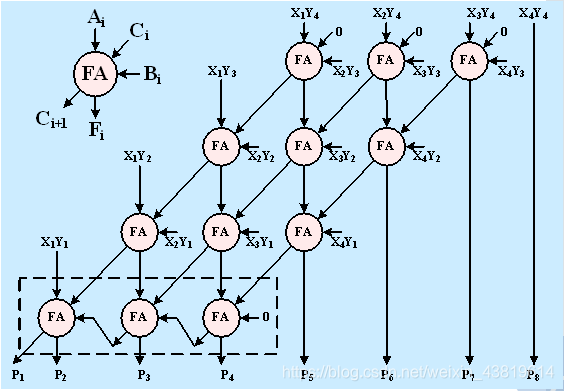
拿老师ppt里的图片用一用了,这是一个4*4的阵列乘法器,可以看到每一层是三个全加器,最后一个也是三位的超前进位加法器。如果要用更高位的阵列乘法器那么也是以此类推。
代码
`timescale 1ns / 1ps
module zhenliechengfa(
input [3:0] x,
input [3:0] y,
output [7:0] z
);
wire c0 = 0;
wire [2:0]cin1=0;
wire [2:0]cin2;
wire [2:0]cin3;
wire [2:0]cin4;
wire [1:0]m4;
wire [1:0]m3;
wire [1:0]m1;
wire [1:0]m2;
wire a1,a2,a3,a4;
lie1 aaa1(.x(x),.y(y[0]),.m(m1),.s(z[0]),.a(a1));
lie234 aaa2(.x(x),.y(y[1]),.cin(cin1),.u(m1),.aa(a1),.s(z[1]),.m(m2),.a(a2),.cout(cin2));
lie234 aaa3(.x(x),.y(y[2]),.cin(cin2),.u(m2),.aa(a2),.s(z[2]),.m(m3),.a(a3),.cout(cin3));
lie234 aaa4(.x(x),.y(y[3]),.cin(cin3),.u(m3),.aa(a3),.s(z[3]),.m(m4),.a(a4),.cout(cin4));
chaoqian3 aaa5(.c0(c0),.x({a4,m4[1],m4[0]}),.y(cin4),.sum({z[6],z[5],z[4]}),.cout(z[7]));
endmodule
顶层模块阵列乘法器中间wire了一些中间变量后续会说。输入是两个4位的x和y因为是四位的阵列乘法器,那么输出就应该是8位的z。
1.中间的一些模块分别是lie1,我用于计算第一层输入值单独写的一个列。
2.lie234是后续每层带3个fa的列。
3.chaoqian3是3位的超前进位加法器。
模块lie1
module lie1(input [3:0]x,input y,output [1:0]m,output s,output a);
and(s,x[0],y);
and(m[0],x[1],y);
and(m[1],x[2],y);
and(a,x[3],y);
endmodule
模块lie1其实就是四个与门但是在阵列乘法器的第一个带有三个fa的阵列之前输入的是x与最低位y分别与出来的值(可以看上面的原理图最顶上的X1Y4),因此将这个过程用一个模块表示,并且将输出用不同的方式表示与后续相同。也就是output a就是直接输出最后一位的真值,2位字长的m代表中间的两个输出,要用于下一个整列的输入,a代表第一个值,看原理图可以发现,每一个阵列的第一个全加器的输入都是单独的,因此将四个与门的值做不同的方式输出,用于后续模块。
模块lie234
module lie234(input [3:0]x,input y,input [2:0]cin,input [1:0]u,input aa,
output s,output [1:0]m,output a,output [2:0]cout);
wire [2:0]bi;
and(bi[0],x[0],y);
and(bi[1],x[1],y);
and(bi[2],x[2],y);
and(a,x[3],y);
fa u1(.a(u[0]),.b(bi[0]),.cin(cin[0]),.sum(s),.cout(cout[0]));
fa u2(.a(u[1]),.b(bi[1]),.cin(cin[1]),.sum(m[0]),.cout(cout[1]));
fa u3(.a(aa),.b(bi[2]),.cin(cin[2]),.sum(m[1]),.cout(cout[2]));
endmodule
首先每个全加器阵列需要在该层有输入,也就是既要有上一层的输出也要有这一层输入所以先用四个与门算出值并保存,用a输出下一层需要单独输入的值。然后使用三个全加器求出两外三个值按照之前说的传给下一层,2位字长的m和该阵列输出的真值s。输入的话有三位的进位标志cin,2位的u表示上一层的2位的m输出,aa表示上一层单独的输出a。
fa是全加器。
模块超前进位加法器
module chaoqian3(input c0,input [2:0]x,input [2:0]y,output [2:0]sum,output cout);
wire [2:0]c;
chaoqianjinwei add3(x,y,c,c0);
wire [2:0]u;
fa U1(.cout(u[0]),.sum(sum[0]),.a(x[0]),.b(y[0]),.cin(c0));
fa U2(.cout(u[1]),.sum(sum[1]),.a(x[1]),.b(y[1]),.cin(c[0]));
fa U3(.cout(u[2]),.sum(sum[2]),.a(x[2]),.b(y[2]),.cin(c[1]));
assign cout=c[2];
endmodule
如果你要做阵列乘法器了那超前进位应该早就学了,我这里就不展开了。
超前进位加法器里调用了超前进位模块,在后面。
超前进位模块
module chaoqianjinwei(x,y,c,c0);
input c0;
input [2:0]x;
input [2:0]y;
output [2:0]c;
wire [2:0]G,P;
assign P = x | y;
assign G = x & y;
assign c[0]= G[0] | (c0&P[0]);
assign c[1]= G[1] | (P[1]&G[0]) | (P[1]&P[0]&c0);
assign c[2]= G[2] | (P[2]&G[1]) | (P[2]&P[1]&G[0]) | (P[2]&P[1]&P[0]&c0);
endmodule
以及最后一个模块全加器
module fa(
input a,
input b,
input cin,
output sum,
output cout
);
wire S1, T1, T2, T3;
xor x1 (S1, a, b);
xor x2 (sum, S1, cin);
and A1 (T3, a, b );
and A2 (T2, b, cin);
and A3 (T1, a, cin);
or O1 (cout, T1, T2, T3 );
endmodule
仿真文件
`timescale 1ns / 1ps
module zhenlie(
output [7:0] z
);
reg [3:0]x;
reg [3:0]y;
initial
begin x=0;y=0;
end
always #3 x=x+1;
always #2 y=y+1;
zhenliechengfa a1(.x(x),.y(y),.z(z));
endmodule
我这里单纯的通过错时对每个加一来遍历所有情况。偷懒orz
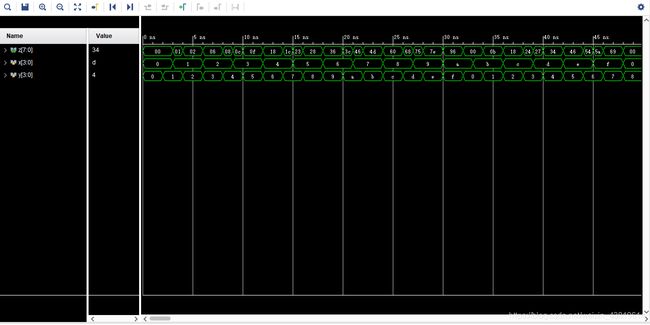
仿真波形如上。
最后附上全部代码
`timescale 1ns / 1ps
module zhenliechengfa(
input [3:0] x,
input [3:0] y,
output [7:0] z
);
wire c0 = 0;
wire [2:0]cin1=0;
wire [2:0]cin2;
wire [2:0]cin3;
wire [2:0]cin4;
wire [1:0]m4;
wire [1:0]m3;
wire [1:0]m1;
wire [1:0]m2;
wire a1,a2,a3,a4;
lie1 aaa1(.x(x),.y(y[0]),.m(m1),.s(z[0]),.a(a1));
lie234 aaa2(.x(x),.y(y[1]),.cin(cin1),.u(m1),.aa(a1),.s(z[1]),.m(m2),.a(a2),.cout(cin2));
lie234 aaa3(.x(x),.y(y[2]),.cin(cin2),.u(m2),.aa(a2),.s(z[2]),.m(m3),.a(a3),.cout(cin3));
lie234 aaa4(.x(x),.y(y[3]),.cin(cin3),.u(m3),.aa(a3),.s(z[3]),.m(m4),.a(a4),.cout(cin4));
chaoqian3 aaa5(.c0(c0),.x({a4,m4[1],m4[0]}),.y(cin4),.sum({z[6],z[5],z[4]}),.cout(z[7]));
endmodule
module lie1(input [3:0]x,input y,output [1:0]m,output s,output a);
and(s,x[0],y);
and(m[0],x[1],y);
and(m[1],x[2],y);
and(a,x[3],y);
endmodule
module lie234(input [3:0]x,input y,input [2:0]cin,input [1:0]u,input aa,
output s,output [1:0]m,output a,output [2:0]cout);
wire [2:0]bi;
and(bi[0],x[0],y);
and(bi[1],x[1],y);
and(bi[2],x[2],y);
and(a,x[3],y);
fa u1(.a(u[0]),.b(bi[0]),.cin(cin[0]),.sum(s),.cout(cout[0]));
fa u2(.a(u[1]),.b(bi[1]),.cin(cin[1]),.sum(m[0]),.cout(cout[1]));
fa u3(.a(aa),.b(bi[2]),.cin(cin[2]),.sum(m[1]),.cout(cout[2]));
endmodule
module chaoqian3(input c0,input [2:0]x,input [2:0]y,output [2:0]sum,output cout);
wire [2:0]c;
chaoqianjinwei add3(x,y,c,c0);
wire [2:0]u;
fa U1(.cout(u[0]),.sum(sum[0]),.a(x[0]),.b(y[0]),.cin(c0));
fa U2(.cout(u[1]),.sum(sum[1]),.a(x[1]),.b(y[1]),.cin(c[0]));
fa U3(.cout(u[2]),.sum(sum[2]),.a(x[2]),.b(y[2]),.cin(c[1]));
assign cout=c[2];
endmodule
module chaoqianjinwei(x,y,c,c0);
input c0;
input [2:0]x;
input [2:0]y;
output [2:0]c;
wire [2:0]G,P;
assign P = x | y;
assign G = x & y;
assign c[0]= G[0] | (c0&P[0]);
assign c[1]= G[1] | (P[1]&G[0]) | (P[1]&P[0]&c0);
assign c[2]= G[2] | (P[2]&G[1]) | (P[2]&P[1]&G[0]) | (P[2]&P[1]&P[0]&c0);
endmodule
module fa(
input a,
input b,
input cin,
output sum,
output cout
);
wire S1, T1, T2, T3;
xor x1 (S1, a, b);
xor x2 (sum, S1, cin);
and A1 (T3, a, b );
and A2 (T2, b, cin);
and A3 (T1, a, cin);
or O1 (cout, T1, T2, T3 );
endmodule
奥里给,干了!