深度学习(1)--基础概念

一.计算机视觉(CV)

(1).计算机视觉中图像表示为三位数组，其中三维数组中像素的值为0~255，像素的值越低表示该点越暗，像素的值越高表示该点越亮。

(2).图像表示 A*B*C，其中A,B分别为图像的长和宽，C则表示图像的颜色通道。

eg: 300*100*3 表示该图像的高度为300，宽度为100，颜色通道为3，即表示该图像有三个颜色通道。(RGB)

二.神经网络基础

1.得分函数：

(1).输入的图片经过得分函数获得对应每个类别的得分，其中x为图片参数，W为权重值参数。

(2).对于32x32x3的图片，一共有3072个像素点，所以像素点矩阵应当是一个3072x1大小的二维矩阵，而每个像素点对应一个权重值，所以权重值矩阵应当是一个1x3072大小的二维矩阵，两个矩阵相乘就可以得到对应该图片类别的一个得分。

(3).b为偏置项，其中W权重参数对结果起决定性作用，b偏置参数对结果进行微调。(b的矩阵大小和得分的矩阵大小相同，对于不同的类别分别进行不同的微调）

eg：将图片分为四个像素点，并选中三个类别图片的权重获取得分值的计算方法：

权重中正值表促进效果，负值表抑制效果，正值越大即对图像的决定性作用越强。

 2.损失函数：

损失函数（loss function）就是用来度量模型的预测值f(x)与真实值Y的差异程度的运算函数，它是一个非负实值函数，通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。

损失函数使用主要是在模型的训练阶段，每个批次的训练数据送入模型后，通过前向传播输出预测值，然后损失函数会计算出预测值和真实值之间的差异值，也就是损失值。得到损失值之后，模型通过反向传播去更新各个参数，来降低真实值与预测值之间的损失，使得模型生成的预测值往真实值方向靠拢，从而达到学习的目的。

eg:根据前一步得分函数计算出的得分值通过损失函数来计算损失值

损失函数 = 数据损失 (有多种计算方法）+ 正则化惩罚项(防止过拟合的情况出现）

过拟合：预测值和样本标签值几乎完全一致的情况，损失函数极小但泛化性能差。训练集的损失函数值很小，但是验证集/测试集上的损失函数值很大。

3.前向传播：

传播过程：将得分值转化为概率值再转换为损失值

(1).exp操作是对数进行指数运算()。

(2).normalize归一化计算，将前一步计算出的值转化为概率。

(3).通过对数函数将概率值转化为损失值。

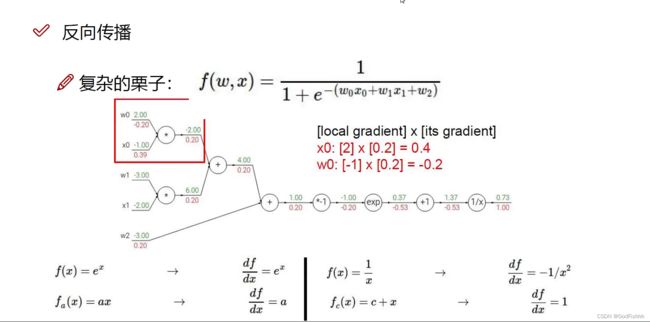
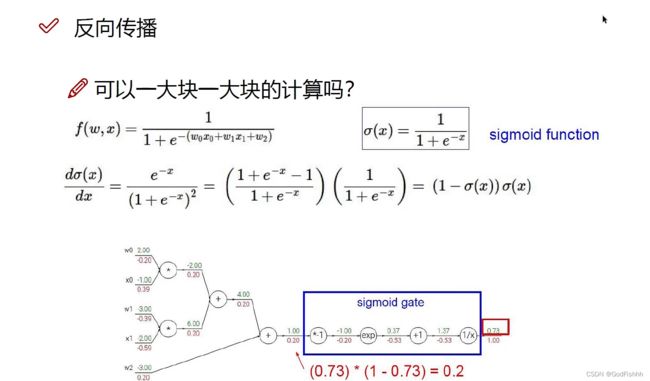
4.反向传播：

反向传播通过导数链式法则计算损失函数对各参数的梯度，并根据梯度进行参数的更新。

损失对参数梯度的反向传播可以被这样直观解释：由A到传播B，即由 ∂L/∂A 得到 ∂L/∂B ，由导数链式法则 ∂L/∂B=(∂L/∂A)⋅(∂A/∂B) 实现。所以神经网络的BP(Back-propagation)就是通过链式法则求出 L对所有参数梯度的过程。

可以一步一步的计算梯度值，也可以取一整块计算梯度值。

反向传播中的常见门单元：

(1).加法门单元：例如对式子x+y求梯度，分别对x和y求偏导得到的值都是1，所以得到的梯度值均为1*后一个式子计算出的梯度值，相当于均等分配。

(2).MAX门单元：将梯度传给最大的值。

(3).乘法门单元：例如对式子x*y求梯度，分别对x和y求偏导得到的是y和x，所以得到的梯度值分别为y*后一个式子计算出的梯度值以及x*后一个式子的梯度值，相当于互换梯度值。

三.神经网络整体架构

生物模型→数学模型

(1).隐藏层hidden layer1保存着由原始特征转化成的计算机能够识别的特征值。

(2).输入层input layer到隐藏层hidden layer的变化通过矩阵相乘实现，其中输入层矩阵所乘的矩阵即为权重矩阵。eg: I[1x3] X W[3x4] = H[1x4]

(3).hidden layer2保存着对hidden layer1的特征值进一步加工得到的特征值。此时应当乘一个4x4大小的权重矩阵。

(4).最后一步由隐藏层到输出层，其中同样乘以相应的权重矩阵。此时应当乘以一个4x1大小的权重矩阵。

(5).神经元个数越多，效果一般来说会越好，但是要避免过拟合等问题。

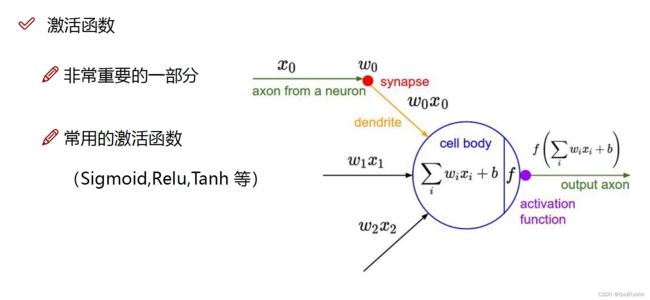
激活函数：

激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。在神经元中，输入的input经过一系列加权求和后作用于另一个函数，这个函数就是这里的激活函数。

神经网络中每一层的输入输出都是一个线性求和的过程，下一层的输出只是承接了上一层输入函数的线性变换，所以如果没有激活函数，那么无论你构造的神经网络多么复杂，有多少层，最后的输出都是输入的线性组合，纯粹的线性组合并不能够解决更为复杂的问题。而引入激活函数之后，我们会发现常见的激活函数都是非线性的，因此也会给神经元引入非线性元素，使得神经网络可以逼近其他的任何非线性函数，这样可以使得神经网络应用到更多非线性模型中。 (在每一层对input值进行权重值的线性计算后再进行激活函数的非线性计算，给下一层的神经元引入非线性元素）