Lecture05：随机市场出清

目录

1 电力市场的不确定性

 2. 随机市场出清问题

2.1 数学模型

 2.2 GAMS计算源码

2.3 计算结果

 3 随机市场出清模型的均衡形式

4 基于场景的随机规划

---

本系列已发表文章列表：

​​​​​​Lecture01：市场出清问题的优化建模

Lecture1b: 如何由原始线性规划模型得到最优条件和对偶问题

Lecture02：均衡问题-优化问题以及KKT等价

Lecture03: 市场出清机制的理想特性

---

先提供两本参考教材：

1. Conejo, A. J., Carrión, M., & Morales, J. M. (2010). Decision making under uncertainty in electricity markets (Vol. 1, pp. 376-384). New York: Springer.
2. Morales, J. M., Conejo, A. J., Madsen, H., Pinson, P., & Zugno, M. (2013). Integrating renewables in electricity markets: operational problems (Vol. 205). Springer Science & Business Media.

1 电力市场的不确定性

电力市场的目标是：在最大化社会福利（或最小化总运作成本）条件下满足需求。

然而，由于可再生能源的发展，为供电系统带来了不确定性：例如，不准确的产量预测会导致错误的承诺和调度决策，从而导致总系统运作成本的提升。那么，如何处理可再生能源带来的不确定性呢？

 将问题分为两个阶段，在DA阶段，使用预测的载荷和风量，来平衡供需；在RT阶段，使用真实的载荷和风量来处理其中的不平衡部分。

下面，我们举一个例子，发电厂G1是发电量和成本是确定的，G2是完全灵活的，WP则是实时地；对于用电企业的需求是确定且没有弹性的，如果不被满足，将会受到一定的惩罚。

 如果风电场的发电量为30MW，则两个阶段解的情况为：

 尽管我们有很多高级的预测方法，但是预测仍旧是有偏差的；下面，我们考虑以下DA阶段不完美的情况，如果我们错误的预测风电发电量为60MW，则有：

 更有甚者，我们预测风电发电量为70MW：

 上面的情况，都是积极地预测。如果决策者比较保守时，如预测风电发电量为10MW:

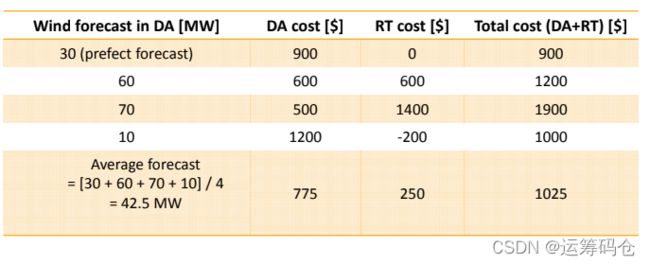
 总结上述几种情况，我们有：

 在DA阶段，我们不知道风量，我们到底应该使用哪个数值呢？一种方法是，我们可以给所有场景都赋值一个权重或发生的概率。这种方法也被称为Look-ahead策略。

 在确定的市场机制中，DA阶段，市场出清是基于真实的风电量预测值；RT阶段，市场出清是根据真实的风电量场景实例。

在随机版本中，DA阶段，市场出清是基于随机的风电量预测值；RT阶段，市场出清是根据真实的风电量场景实例，但它并不必是其中任意一个场景实例。

 2. 随机市场出清问题

我们的市场出清问题就转化为：

参考文献：

1.  Pritchard, G., Zakeri, G., & Philpott, A. (2010). A single-settlement, energy-only electric power market for unpredictable and intermittent participants. Operations research, 58(4-part-2), 1210-1219.
2. Morales, J. M., Conejo, A. J., Liu, K., & Zhong, J. (2012). Pricing electricity in pools with wind producers. IEEE Transactions on Power Systems, 27(3), 1366-1376.

2.1 数学模型

 回到刚开始的例子，我们可以建立如下随机规划模型：

 求解上述模型，我们可以得到如下解决方案：

 2.2 GAMS计算源码

sets
i conventional generators /i1*i2/
d inelastic loads /d1/
n buses /n1*n2/
s scenarios /s1*s4/
k wind power generators / k1/
slack(n) /n1/
Mapi(i,n) /i1.n1, i2.n2/
Mapd(d,n) / d1.n1/
Mapnm(n,n) / n1.n2, n2.n1/
Mapk(k,n) / k1.n2/
alias (n,m);

parameters
W_max(k) wind power installed capacity;
parameters
phi(s) probability of scenarios /
s1 0.25
s2  0.25
s3  0.25
s4 0.25/

L(d) Load level /d1 120/
V(d) Value of lost load /d1 80/ ;

TABLE GDATA(i,*) generators' input data
    Pmax    C   Rmax
i1  100     10  0
i2  30      20  30;
Table W(k,s) wind realizatio under different scenarios
    s1  s2  s3  s4
k1  30  60  70  10;
Table Fmax(n,n) Transmission lines capacity
    n1  n2
n1  0   100
n2  100 0;
Table B(n,n) Transmission lines susceptance
    n1  n2
n1  0   500
n2  500 0;
W_max(k)=70;

variables
cost Total expected system cost (DA + RT)
theta_DA(n) voltage angles in DA
f_DA(n,m) Power flows in DA
f_RT(n,m,s) Power flows in RT
theta_RT(n,s) voltage angles in RT
time CPU time
r(i,s) Power adjustment of generator i in RT under scenario s;

positive variables
L_shed(d, s) curtailed load
P(i) DA dispatch of generators
P_W(k) wind dispatch in DA
P_spill(k, s) wind spillage;

equations
costfn, node_DA, Pmax, kmax, flow_DA, flow_max_DA, slack_DA, node_RT,
RUmax, RDmax, generation_min, generation_max, flow_RT, flow_max_RT,
shedding, spillage, slack_RT;
costfn.. cost =e= sum(s, phi(s)*{[sum(i,GDATA(i,'C')*r(i,s))]
                                +[sum(d,v(d)*L_shed(d,s))]})
                                +[sum(i,GDATA(i,'C')*P(i))];
* DAconstraints
node_DA(n).. sum(i$Mapi(i,n),P(i))+sum(k$Mapk(k,n),P_w(k))
                                  -sum(d$Mapd (d,n),L(d) )
                                  -sum(m$Mapnm(n,m),f_DA(n,m) ) =e= 0;
Pmax(i).. P(i) =l= GDATA(i,'Pmax');
kmax(k).. P_w(k)=l=w_max(k);
flow_DA(n,m)$Mapnm(n,m).. f_DA(n,m) =e= B(n,m)*(theta_DA(n)-theta_DA(m));
flow_max_DA(n,m)$Mapnm (n,m).. f_DA(n,m) =l= Fmax(n,m);
slack_DA.. theta_DA('n1') =e= 0;

* RT constraints
node_RT(n,s).. sum(i$Mapi(i,n),r(i,s))
                +sum(k$Mapk(k,n),w(k,s)-P_w(k)-P_spill(k,s))
                +sum (d$Mapd(d,n),L_shed(d,s))
                -sum(m$Mapnm(n,m),f_RT(n,m,s)-f_DA(n,m)) =e= 0;
RUmax(i,s).. r(i,s) =l= +GDATA(i,'Rmax');
RDmax(i,s).. r(i,s) =g= -GDATA(i,'Rmax');
generation_min(i,s).. [P(i)+r(i,s)] =g= 0;
generation_max(i,s).. [P(i)+r(i,s)] =l= GDATA(i,'Pmax');
flow_RT(n,m,s)$Mapnm(n,m).. f_RT(n,m,s) =e= B(n,m)*(theta_RT(n,s)-theta_RT(m,s));
flow_max_RT(n,m,s)$Mapnm(n,m).. f_RT(n,m,s) =l= Fmax(n,m);
shedding(d,s).. L_shed(d,s) =l= L(d);
spillage(k,s).. P_spill(k,s) =l= w(k,s);
slack_RT(s).. theta_RT('n1',s) =e=0;

model stochastic_clearing / all / ;
solve stochastic_clearing using lp minimizing cost;
time.l = stochastic_clearing.resusd;
parameters
LambdaN_DA(n)
LambdaN_RT(n,s);
LambdaN_DA(n) = node_DA.m(n);
LambdaN_RT(n,s) = node_RT.m(n,s)/phi(s);
display
cost.l,LambdaN_DA,LambdaN_RT,P_W.l,P.l,r.l,p_spill.l,L_shed.l,time.l;

2.3 计算结果

 3 随机市场出清模型的均衡形式

 

 在我们的问题中，随机出清问题的优化形式和均衡形式都能导出同样的KKT条件，因此两个模型是等价的。

但是在现实模型中，很少使用随机模型，这主要是因为：

1. 计算问题，你需要多少场景来描述问题呢？
2. 很难确定每个场景的概率，是的市场的设计变得更加复杂化。
3. 随机市场失去了市场应有的属性

是否存在一种机制，对确定性模型进行改善，以使得确定性问题的解接近随机版本。

4 基于场景的随机规划

方法步骤：

1. 生成大于100个场景对不确定参数进行建模
2. 选择部分场景，如随机选择20%，作为训练场景，求解随机问题
3. 用剩余的数据作为测试数据，执行样本外分析（out‐of‐sample analysis）
4. 根据期望值和标准差比较上述两种分析中获得的目标函数值
5. 分析选择方法和样本内的数量是如何影响样本外结果的

生成随机场景的方法：

1. 蒙特采样
2. 基于历史数据的随机模拟
3. 基于分布的均匀采样

选择样本内场景：

1. 基于聚类的方法，如K-means，选出最有代表性的个体
2. 认为所有场景是无差别的，随机选择

 你需要测试样本内得到的结果与样本外得到的结果有多接近，如果两者偏差很大，那么问题出在以下两方面：

1. 选择的样本内数量不合适，需要测试其他的 样本内数量；如上图中，将50变成60,70或150等
2. 选择的样本代表性不足，需要变更 样本内样本集；例如，另外再选择50个更好的样本作为训练集