【LGR-172-Div.4】洛谷入门赛 #19（A—H,c++详解！）

---

【LGR-172-Div.4】洛谷入门赛 #19

A.分饼干 I

题目描述

洛谷网校举行了期末考试，同学们经过课程的学习，考出了优异的成绩。

Z 在考试中获得了第一名，yz 在考试中获得了第二名，老师决定买一些饼干奖励两名小朋友。

老师买了三盒饼干，第一盒有 $a$ 块饼干，第二盒有 $b$ 块饼干，第三盒有 $c$ 块饼干。老师决定将这三盒饼干奖励给 Z 和 yz，三盒饼干不可以被拆开奖励。

老师希望 Z 拿到的饼干块数不少于 yz，但又希望两人拿到的饼干数量差距尽可能小，请问 Z 和 yz 各拿到几块饼干？

输入格式

输入一行三个整数，分别为 $a,b,c$。

输出格式

输出一行两个整数，由空格分隔。第一个整数代表 Z 拿到的饼干数量，第二个整数代表 yz 拿到的饼干数量。

样例 #1

样例输入 #1

3 1 5

样例输出 #1

5 4

样例 #2

样例输入 #2

3 3 5

样例输出 #2

6 5

提示

样例解释 1

Z 拿走 $5$ 块饼干，yz 拿走 $3+1=4$ 块饼干。

样例解释 2

Z 拿走 $3+3=6$ 块饼干，yz 拿走 $5$ 块饼干。

数据范围与约定

• 对于 $30\%$ 的测试数据，$a=b=c$；
• 对于 $100\%$ 的测试数据，$1\le a,b,c\le 1000$。

思路:

题目有两个要求，最重要的是Z 拿到的饼干块数不少于 yz！！！在满足前者的前提下第二个要求是希望两人拿到的饼干数量差距尽可能小。

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
int a[4];

void solve(){
    repn(i,1,3) cin>>a[i];
    sort(a+1,a+4);
	int ans1,ans2;
	if(a[1]+a[2]!=a[3]){//两个小的加起来和最大的不相等,取较大值的已给第一名
		if(a[1]+a[2]>a[3]){
			ans1=a[1]+a[2];
			ans2=a[3];
		}else{
			ans1=a[3];
			ans2=a[1]+a[2];
		}
	}else{//！！！两者相等时，题目要求了Z 拿到的饼干块数不少于 yz
		ans1=a[3]+a[1];//有要求两者差距尽可能小，所以我们拿一个最大的和一个最小的
		ans2=a[2];
	}
	cout<<ans1<<' '<<ans2;
} 

signed main(){
//	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

B.分饼干 II

题目描述

老师有 $N$ 块饼干，要分给 $k$ 名小朋友。

每名小朋友至少拿到一块饼干，老师想让每名小朋友拿到的饼干数量都不一样多，请问老师能否实现这个目标。

输入格式

本题单个测试点内有多组测试数据。

输入共 $T+1$ 行。

输入第一行为一个整数 $T$，代表测试数据组数。
接下来 $T$ 行，每行两个整数，分别为 $N,k$。

输出格式

输出共 $T$ 行，依次对应 $T$ 组测试数据。如果该组测试数据

• 可以实现，输出 Yes。
• 无法实现，输出 No。

样例 #1

样例输入 #1

1
1 1

样例输出 #1

Yes

样例 #2

样例输入 #2

1
5 3

样例输出 #2

No

提示

数据规模与约定

• 对于 $50\%$ 的测试数据 $1\le k\le 1000$，$1\le N\le 10^6$。
• 对于 $100\%$ 的测试数据，$1\le k,N\le 10^9$。

思路

• 题意大概是N块饼干分给k个小朋友，每个小朋友至少拿一块饼干，并且，内每个小朋友拿到的饼干数量都不一样。
• 既然每个小朋友分到的数量都不一样，那我们不妨从1个饼干开始分，1，2，3，······，k. 这样就保证了每个小朋友分到的数量都不一样。不难发现这是一个等差数列，我们根据等差数列求和公式得到总和sum,如果sum>n,说明饼干太少啦＞﹏＜，根本不够分啊！如果sum<=n,我们就可以分成k份，保证了两两各不相同。

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 

void solve(){
    int n,k;
    cin>>n>>k;
    if(n==1) {//注意特判一下
	  cout<<"Yes"<<endl;
	  return ;
    }  
    int sum=(1+k)*k/2;
    if(sum>n) cout<<"No"<<endl;
    else cout<<"Yes"<<endl;
	
		
} 

signed main(){
//	IOS;
	int T=1;
	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

C.跳房子

题目背景

跳房子，也叫跳飞机，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一，趣味性、娱乐性极强，曾深受广大儿童的喜爱。

题目描述

现在我们给出一种简易跳房子游戏的玩法：

$n$ 个格子从左到右一字形排开，从左到右依次被标号为 $1,2,\cdots ,n$。每一个格子上都有一个正整数，$i$ 号格子上的正整数是 $a_i$。

这个游戏的规则如下：初始时玩家站在 $1$ 号格子上，需要做若干次跳跃。每一次跳跃时，玩家需要从当前格子向前跳「当前格子上写的整数」数量的格子。形式化地讲，如果玩家当前处于 $x$ 号格子，玩家需要跳到 $x+a_x$ 号格子上。

如果玩家跳到 $n$ 号格子右侧的位置，称玩家出界；如果玩家恰好跳到 $n$ 号格子上，称玩家胜利。这两种情况下玩家都需要停止跳跃。

现在给定格子数量和格子上的整数，你需要求解：

1. 在停止跳跃后，玩家是否胜利。即，玩家是否能够恰好跳到 $n$ 号格子上。
2. 在停止跳跃后，玩家跳跃的总次数。

输入格式

输入共两行。

第一行为一个整数 $n$，代表格子的数量。
第二行为 $n$ 个整数 $a_1,a_2,\cdots ,a_n$，代表每个格子上的数字。

输出格式

输出共两行。

第一行为一个字符串。如果玩家在停止跳跃后恰好跳到 $n$ 号格子上，输出 Yes，否则输出 No。
第二行一个整数，代表玩家的总跳跃次数。

样例 #1

样例输入 #1

6
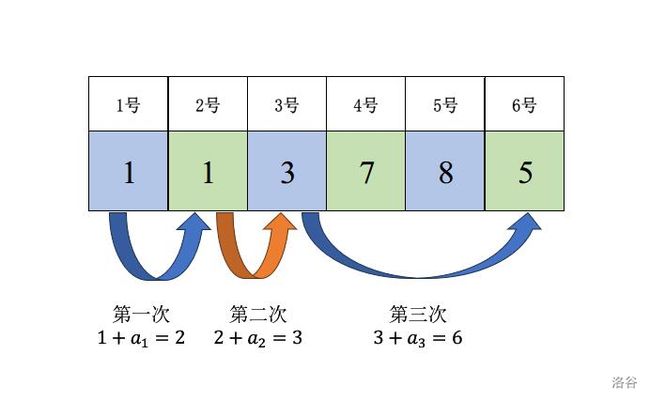
1 1 3 7 8 5

样例输出 #1

Yes
3

样例 #2

样例输入 #2

4
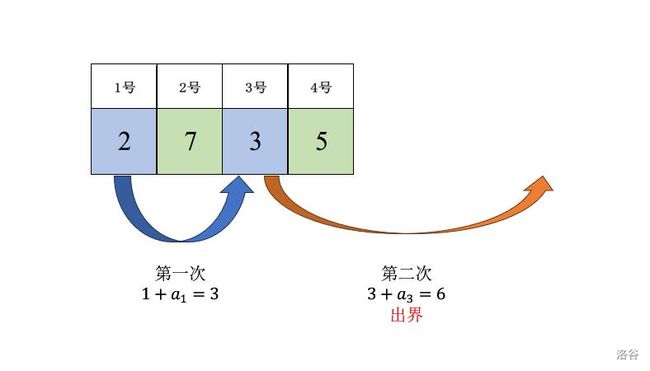
2 7 3 5

样例输出 #2

No
2

提示

样例 1 解释

样例 2 解释

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 10^6$，$1\le a_i\le 10^4$。

测试点编号	$n$	特殊性质
$1$	$=1$	无
$2\sim 4$	$\le 100$	无
$5$	$\le 10^6$	$a_i=1$
$6,7$	$\le 10^6$	$a_i=2$
$8\sim 10$	$\le 10^6$	无

思路

模拟题，按照题目要求模拟即可，具体步骤请看代码

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 2e6+10, INF=1e18+10;
int a[N];

void solve(){
    int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	int res=0,i=1,now=1;
	if(n==1){//特判！！！
		cout<<"Yes"<<endl;
		cout<<0<<endl;
		return ;
	}
	while(1){
		now+=a[i];//移动a[i]步
		i+=a[i];//注意下标也要加a[i]
		res++;//步数加1
		if(now==n){//到达终点，游戏结束！
			cout<<"Yes"<<endl;
			cout<<res;
		    return;
		}
		//cout<
		if(now>n) break;//越界，游戏结束！
	}
 	cout<<"No"<<endl;
 	cout<<res;
} 

signed main(){
//	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

D 区间函数最小值

题目描述

给定 $A,B,C,D,E,F,G,P,X_1,X_2,Y_1,Y_2$，求当 $X_1\le x\le X_2$，$Y_1\le y\le Y_2$ 且 $x,y$ 均为整数时

$$f(x,y)=(A{x}^3+B{y}^3+C{x}^{2}y+Dx{y}^2+Exy+Fx+Gy)\mathrm{mod}P$$

的最大值。

输入格式

输入共一行十二个整数 $A,B,C,D,E,F,G,P,X_1,X_2,Y_1,Y_2$。

输出格式

输出一个整数，代表 $f(x,y)$ 的最大值。

样例 #1

样例输入 #1

3 2 5 6 1 4 2 998244353 1 2 1 3

样例输出 #1

266

提示

样例解释 #1

当 $x$ 为 $1$ 到 $2$ 之间的整数，$y$ 为 $1$ 到 $3$ 之间的整数时，函数 $f(x,y)$ 的值如下：

$$\begin{gathered} f(1,1)=23,f(1,2)=63,f(1,3)=139 \\ f(2,1)=70,f(2,2)=144,f(2,3)=266 \end{gathered}$$

最大值为 $f(2,3)$，即 $266$。

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le A,B,C,D,E,F,G,P\le 10^9$，$1\le X_1\le X_2\le 10^3$，$1\le Y_1\le Y_2\le 10^3$。

思路

遍历一遍（x,y)即可，刚开始以为是个数论题哈哈，吓得直接跳过了，回头一看数据范围x,y只有1e3，也就是说暴力的话时间复杂度为O(n^2),1e6不会超时间限制！

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 2e5+10, INF=1e18+10;
int a,b,c,d,e,f,g,p,X1,X2,Y1,Y2;

int calc(int x,int y){
	return (a*x*x*x+b*y*y*y+c*x*x*y+d*x*y*y+e*x*y+f*x+g*y)%p; 
}

void solve(){
    cin>>a>>b>>c>>d>>e>>f>>g>>p>>X1>>X2>>Y1>>Y2;
    int res=0;
    for(int i=X1;i<=X2;i++)
      for(int j=Y1;j<=Y2;j++){
      	res=max(res,calc(i,j));
	  }
	cout<<res<<endl;
		
} 

signed main(){
//	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

E.小跳蛙

题目背景

idea 提供者： bj12z_jiasiyuan

验题：卷王

题目描述

有 $n-1$ 只小跳蛙在池塘中，依次被编号为 $1,2,\cdots ,n-1$。池塘里有 $n$ 个位置，每一个位置上有一个数字 $a_i$。如果 $a_i=0$，则表示这个位置是一个空位；否则表示这个位置上存在一个编号为 $a_i$ 的小跳蛙。

接下来的 $n-1$ 分钟，小跳蛙们将进行跳跃。第 $i$ 分钟，编号为 $i$ 的小跳蛙将跳到空位上。

请你输出 $n-1$ 分钟后池塘中每个位置的数字，即每个位置是否为空、小跳蛙编号是多少。

输入格式

输入共两行。

第一行一个整数 $n$。
第二行 $n$ 个整数 $a_1,a_2,\cdots ,a_n$。

输出格式

输出一行 $n$ 个整数 $a_1,a_2,\cdots ,a_n$。 表示 $n-1$ 分钟后池塘的状态。

样例 #1

样例输入 #1

5
1 2 0 3 4

样例输出 #1

2 3 1 4 0

提示

样例解释 #1

• 第一分钟后池塘状态：0 2 1 3 4
• 第二分钟后池塘状态：2 0 1 3 4
• 第三分钟后池塘状态：2 3 1 0 4
• 第四分钟后池塘状态：2 3 1 4 0

因此最终池塘的状态为 2 3 1 4 0。

数据规模与约定

对于 $50\%$ 的数据，$1\le n\le 10^3$。

对于 $100\%$ 的数据，$1\le n\le 10^6$，保证序列 $a$ 是一个 $0\sim n-1$ 这些数字的排列。

思路

可以用map记录编号对应的下标，第i分钟就让编号为i的蛤蟆与空位（即编号0）交换位置

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 1e6+10, INF=1e18+10;
int n,a[N];
unordered_map<int,int> mp;//编号->下标的映射

void solve(){
    cin>>n;
    for(int i=1;i<=n;i++){
    	cin>>a[i];
    	mp[a[i]]=i;
	}
	for(int i=1;i<=n;i++){
		int x=mp[i];//编号为i的下标
		int y=mp[0];//编号为0的下标
		swap(a[x],a[y]);//交换位置
		mp[0]=x;
		mp[i]=y;
//		for(int i=1;i<=n;i++)
//		cout<

//		cout<
	}
	for(int i=1;i<=n;i++)
		cout<<a[i]<<' ';
} 

signed main(){
	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

F.图像变换

题目描述

一张字符图片由 $n$ 行 $m$ 列，共 $n\times m$ 个字符组成，第 $i$ 行第 $j$ 列的字符为 $s_{i,j}$。如下图所示，为一个 $4\times 3$ 的字符图片。

%%%
$$$
@w@
!!!

现在，需要将图像放大 $k$ 倍，得到 $kn\times km$ 的图片。原图片的每个字符都需要重复 $k^2$ 次，作为新图像中 $k\times k$ 的一个区域，各字符的相对位置不变。

将上面给出的例子放大 $2$ 倍，将得到如下图像：

%%%%%%
%%%%%%
$$$$$$
$$$$$$
@@ww@@
@@ww@@
!!!!!!
!!!!!!

输入格式

输入 $n+1$ 行。

输入的第一行为三个整数 $n,m,k$。

接下来 $n$ 行，每行 $m$ 个字符，表示字符图片。

输出格式

输出 $nk$ 行，每行 $mk$ 个字符，表示变换后的字符图片。

样例 #1

样例输入 #1

4 3 2
%%%
$$$
@w@
!!!

样例输出 #1

%%%%%%
%%%%%%
$$$$$$
$$$$$$
@@ww@@
@@ww@@
!!!!!!
!!!!!!

提示

数据规模与约定

• 对于 $30\%$ 的测试数据，输入的字符画仅包含一种字符；
• 对于 $100\%$ 的测试数据，$1\le n,m\le 100$，$1\le k\le 10$，输入的字符仅包含 ASCII 码不超过 127 的可见字符。

思路

观察样例，我们可以看出每个字符需要输出k次，横纵长度都扩大了k倍

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 2e3+10, INF=1e18+10;
int n,m,k;
char g[N][N];

void solve(){
    cin>>n>>m>>k;
    repn(i,1,n)
     repn(j,1,m) 
       cin>>g[i][j];
    for(int i=1;i<=n;i++){
    	for(int u=1;u<=k;u++){//每个字母输出k次
    	  for(int j=1;j<=m;j++){
    		for(int p=1;p<=k;p++) 
    		  cout<<g[i][j];
		  }  
		  cout<<endl;//注意换行
		}
		
	}	
} 

signed main(){
//	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

G.二进制与一

题目描述

给定一个正整数 $n$，以及操作次数 $q$。对于每次操作，给出一个正整数 $k$，要求：让 $n$ 加上一个非负整数 $x$，使得 $n$ 在二进制下的第 $k$ 位（从右往左数）是 $1$，并在符合要求的情况下，令 $x$ 最小。

请注意，每次操作都会让 $n$ 变为 $n+x$，会影响后续操作。

小山需要求出，所有的 $x$ 之和是多少。

输入格式

输入共 $q+1$ 行。

第一行两个整数 $n$ 和 $q$。
接下来 $q$ 行，每行一个正整数 $k$，表示要让 $n$ 在二进制下从右往左数的第 $k$ 位是 $1$。

输出格式

一行一个整数，表示所有的 $x$ 之和。

样例 #1

样例输入 #1

5 3
2
3
4

样例输出 #1

3

提示

样例 1 说明

$5$ 在二进制下是 $101$。

• 对于第一次操作，需要让 $101$ 的第二位变为 $1$，则需让 $101$ 加上 $1$，变为 $110$；
• 对于第二次操作，需要让 $110$ 的第三位是 $1$，由于 $110$ 的第三位本身就是一，所以无需改变；
• 第三次操作同理，需要让 $110$ 加上 $2$。

最终输出结果是 $1+0+2=3$。

数据规模与约定

对于 $100\%$ 的数据，$1\le n<2^{32}，1\le q\le 10^5，1\le k\le 32$。

测试点编号	$n$	$q$	$k$
$1$	$\le 4$	$\le 10$	$\le 2$
$2,3$	$\le 4$	$\le 10$	$\le 32$
$4,5$	$\le 1024$	$\le 1000$	$\le 10$
$6,7$	$<2^{32}$	$\le 10$	$\le 32$
$8\sim 10$	$<2^{32}$	$\le 10^5$	$\le 32$

思路

考察的二进制位运算，手写一下我们发现我们需要取后k位，那么该怎么取呢？比如n=6,二进制是110去后两位，1<<2是100，此时再减一变为011，在与上n为010，即可取得后两位，取后k位亦是如此。
再用1<<(k-1)减去n的后k位即为让从右往左数的第 k 位变为 1差的值。

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 2e5+10, INF=1e18+10;

void solve(){
    int n,q,sum=0;
    cin>>n>>q;
    while(q--){
    	int k;
    	cin>>k;
    	//cout<
    	if(n&(1LL*1<<(k-1))) continue;//已经是1 
    	int x=(1LL*1<<(k-1))-n&((1LL*1<<k)-1);
    	n+=x;
    	sum+=x;
    	//cout<<"**"<
	}
	cout<<sum;
		
} 

signed main(){
//	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

H.Genshin 玩家

题目背景

你说得对，后面忘了。

题目描述

在洛谷入门赛/语言月赛出题 QQ 群里，著名洛谷管理员蓝边铅球老师的群名片是『原神玩家』。

现在，扶苏给了你一个字符串 $s$，她想请你求出：有多少种方案可以在 $s$ 中取出两个子串 $s[l_1,r_1],s[l_2,r_2]$，满足：

• $1\le l_1\le r_1\le l_2\le r_2\le |s|$，这里 $|s|$ 表示字符串 $s$ 的长度。
• $s[l_1,r_1]$ 表示由 $s$ 的第 $l_1$ 个字符到第 $r_1$ 个字符构成的字符串，$s[l_1,r_1]=\text{Genshin}$。
• $s[l_2,r_2]$ 表示由 $s$ 的第 $l_2$ 个字符到第 $r_2$ 个字符构成的字符串，$s[l_2,r_2]=\text{player}$。

两个方案不同，当且仅当两个方案中 $l_1,r_1,l_2,r_2$ 至少有一个对应不同。

输入格式

输入只有一行，表示字符串 $s$。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

Genshinplayerplayer

样例输出 #1

2

样例 #2

样例输入 #2

ExpectedIsAGenshinplayerWhoLikesToBeAGenshinplayer

样例输出 #2

3

提示

数据规模与约定

• 对 $30\%$ 的数据，保证 $|s|\le 50$。
• 对 $60\%$ 的数据，保证 $|s|\le 200$。
• 对 $100\%$ 的数据，保证 $1\le |s|\le 2000$，$s$ 中仅含大小写英文字母。

思路

主要就是找字串再在主串中出现的次数，先找s1=“Genshin”，然后再找s2="player"出现的次数，然后再找下一个s1,以及下一个s1后面s2出现了多少次，直到找不到s1。这里用find函数来查找子串。其实也可以用kmp算法求字串，不过有点麻烦，属实是杀鸡用牛刀了（￣︶￣）。

代码

#include
using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long 
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 2e5+10, INF=1e18+10;
string s1="Genshin",s2="player";

void solve(){
	string s;
	cin>>s;
	int res=0;
	int pos1=s.find(s1,0);
	while(s.find(s1,pos1)!=-1){
		if(pos1!=-1){
			int pos2=s.find(s2,pos1),num=0;
			while(s.find(s2,pos2)!=-1){
				num++;
				pos2=s.find(s2,pos2+1);
			}
			res+=num; 
//			cout<
		}
		pos1=s.find(s1,pos1+1);
	}	
	cout<<res;
} 

signed main(){
//	IOS;
	int T=1;
//	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}
/*


*/

总结：

本次比赛难度只有div4，但比赛中好几道没有全过，甚至有的只过了两三个点（H）。

• 第一题分饼干I就想了好几分钟，脑子不清醒，写了一堆还有两三个点没过，赛后又想了想发现没有考虑到Z 拿到的饼干块数不少于 yz这个点，属于没认真读题了。
• 第二题想了想可以用等差数列求和做，没卡多久。
• 跳房子模拟就行，wa了两发，下标没有加a[i[值。
• 小跳蛙比赛时没想出来，暴力做了
• 二进制与一推了好久,属于是位运算基础不太行了
• 最后一题思路是对的，但是实现起来出现了问题，对find函数的应用还是不太熟练啊！
• 最后最重要的就是一个字要 稳！！！不能为了赶做题速度，从而落下题目中的关键点，还有就是脑袋要清醒啊，不能迷迷糊糊做题是吧，有的题比赛做不出来，赛后一想就知道思路了，归根结底还是没有深思熟虑！