力扣hot 100 题解记录一
- 力扣hot 100 题解记录第一篇
-
-
- 1. 两数之和
- 2. 两数相加
- 3. 无重复字符的最长子串
- 4. 寻找两个正序数组的中位数⭐⭐
- 5. 最长回文子串⭐
- 10. 正则表达式匹配⭐⭐
- 11. 盛最多水的容器
- 15. 三数之和
- 17. 电话号码的字母组合
- 19. 删除链表的倒数第 N 个结点
- 20. 有效的括号
- 21. 合并两个有序链表
- 22. 括号生成
- 23. 合并K个升序链表⭐⭐
- 31. 下一个排列⭐⭐
- 32. 最长有效括号⭐⭐⭐
- 33. 搜索旋转排序数组
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 39. 组合总和
- 42. 接雨水⭐⭐
-
力扣hot 100 题解记录第一篇
1. 两数之和
链接
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
进阶: 你可以想出一个时间复杂度小于 O(n2) 的算法吗?
思路:
创建一个哈希表,对于每一个 x,我们首先查询哈希表中是否存在 target - x,存在则返回结果,否则将 x 插入到哈希表中。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> map;
int n = nums.size();
for (int i = 0; i < n; i++) {
auto it = map.find(target-nums[i]);
if (it != map.end()) {
return {it->second, i};
}
map[nums[i]] = i;
}
return {};
}
};
class Solution(object):
def twoSum(self, nums, target):
n = len(nums)
map = dict()
for i in range(n):
if target - nums[i] in map:
return [map[target - nums[i]], i]
map[nums[i]] = i
return []
2. 两数相加
链接
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
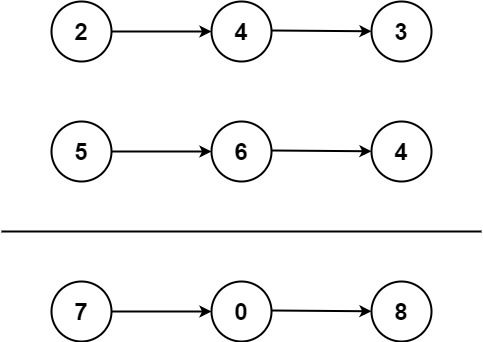
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
思路:
模拟法。由于输入的两个链表都是逆序存储数字的位数的,因此两个链表中同一位置的数字可以直接相加。同时遍历两个链表,逐位计算它们的和,并与当前位置的进位值相加。
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode *head = nullptr, *tail = nullptr;
int carry = 0;
while (l1 || l2) {
int n1 = l1 ? l1->val: 0;
int n2 = l2 ? l2->val: 0;
int sum = n1 + n2 + carry;
if (!head) {
head = tail = new ListNode(sum % 10);
} else {
tail->next = new ListNode(sum % 10);
tail = tail->next;
}
carry = sum / 10;
if (l1) {
l1 = l1->next;
}
if (l2) {
l2 = l2->next;
}
}
if (carry > 0) {
tail->next = new ListNode(carry);
}
return head;
}
};
class Solution(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
p = ans = None
carry = 0
while l1 or l2:
n1 = l1.val if l1 else 0
n2 = l2.val if l2 else 0
if l1:
l1 = l1.next
if l2:
l2 = l2.next
arrsum = n1 + n2 + carry
if not ans:
ans = p = ListNode(arrsum % 10)
else:
p.next = ListNode(arrsum % 10)
p = p.next
carry = arrsum / 10
if carry:
p.next = ListNode(carry)
return ans
3. 无重复字符的最长子串
链接
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
思路:
滑动窗口法。使用l,r作为滑动窗口的左右边界,使用哈希表window存储滑动窗口内存放的字符数量。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
// 使用双指针做滑动窗口
int l = 0, r = 0, n = s.size();
int ans = 0;
unordered_map<char, int> window;
while (r < n) {
char c = s[r++];
window[c]++;
while(window[c] > 1) {
// 收缩区间
char la = s[l++];
window[la]--;
}
ans = max(ans, r - l);
}
return ans;
}
};
class Solution(object):
def lengthOfLongestSubstring(self, s):
cnt = dict()
l, r = 0, 0
ans = 0
while r < len(s):
c = s[r]
r += 1
if cnt.has_key(c):
cnt[c] += 1
else:
cnt[c] = 1
while cnt[c] > 1:
la = s[l]
l += 1
cnt[la] -= 1
ans = max(ans, r - l)
return ans
4. 寻找两个正序数组的中位数⭐⭐
链接
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
思路:
方法一:划分数组。将{A,B} 中的所有元素划分为两个部分,前一部分比后一部分多一个元素,且前一部分中的元素总是小于或等于后一部分中的元素。因此,中位数就是前一部分的最大值,或者前一部分最大值与后一部分最小值的均值。
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
if (m > n) {
return findMedianSortedArrays(nums2, nums1);
}
int totalNums = (m + n + 1) / 2;
int l = 0, r = m;
while (l < r) {
int i = l + (r - l + 1) / 2;
int j = totalNums - i;
if (nums1[i - 1] > nums2[j]) {
r = i - 1;
} else {
l = i;
}
}
int i = l, j = totalNums - i;
int nums1_left = i ? nums1[i - 1] : INT_MIN;
int nums1_right = i == m ? INT_MAX : nums1[i];
int nums2_left = j ? nums2[j - 1] : INT_MIN;
int nums2_right = j == n ? INT_MAX : nums2[j];
if ((m + n) & 1) return max(nums1_left, nums2_left);
return (double) (max(nums1_left, nums2_left) + min(nums1_right, nums2_right)) / 2.0;
}
};
方法二:二分查找。这道题可以转化成寻找两个有序数组中的第 k 小的数,其中 k 为 (m+n)/2 或 (m+n)/2+1。
class Solution {
public:
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
* 这里的 "/" 表示整除
* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
* 这样 pivot 本身最大也只能是第 k-1 小的元素
* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组
* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组
* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数
*/
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// 边界情况
if (index1 == m) {
return nums2[index2 + k - 1];
}
if (index2 == n) {
return nums1[index1 + k - 1];
}
if (k == 1) {
return min(nums1[index1], nums2[index2]);
}
// 正常情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
}
else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1) {
return getKthElement(nums1, nums2, (totalLength + 1) / 2);
}
else {
return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
}
};
5. 最长回文子串⭐
链接
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
思路:
方法一:动态规划
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if (n < 2) return s;
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
vector<vector<int>> dp(n, vector<int>(n));
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= n; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < n; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= n) break;
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, maxLen);
}
};
方法二:中心扩展
class Solution {
public:
pair<int, int> expandAroundCenter(const string& s, int left, int right) {
while (left >= 0 && right < s.size() && s[left] == s[right]) {
--left;
++right;
}
return {left + 1, right - 1};
}
string longestPalindrome(string s) {
int start = 0, end = 0;
for (int i = 0; i < s.size(); ++i) {
auto [left1, right1] = expandAroundCenter(s, i, i);
auto [left2, right2] = expandAroundCenter(s, i, i + 1);
if (right1 - left1 > end - start) {
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {
start = left2;
end = right2;
}
}
return s.substr(start, end - start + 1);
}
};
方法三:马拉车算法
class Solution {
public:
string longestPalindrome(string s) {
int start = 0, end = -1;
string t = "#";
for (char c: s) {
t += c;
t += '#';
}
// 存储以该值为中心的最大半径长度
int pArr[t.size()];
// 保存每一次的中心和最右端索引
int C = -1, R = -1;
int ansC = 0;
for (int i = 0; i < t.size(); i++) {
// 判断是否在之前的内部。在:利用之前初始化现在的;不在:初始化为1,即自身;
pArr[i] = R > i ? min(pArr[2 * C - i], R - i) : 1;
while(i + pArr[i] < t.size() && i - pArr[i] > -1){
// 使用中心扩散
if(t[i + pArr[i]] == t[i - pArr[i]])
pArr[i]++;
else{
break;
}
}
if (i + pArr[i] > R){
// 更新R C
R = i + pArr[i];
C = i;
}
if (pArr[ansC] < pArr[i]) ansC = i;
}
return s.substr((ansC - pArr[ansC] + 2) / 2, pArr[ansC] - 1);
}
};
10. 正则表达式匹配⭐⭐
链接
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab", p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
提示:
1 <= s.length <= 201 <= p.length <= 30s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。- 保证每次出现字符
*时,前面都匹配到有效的字符
思路:
动态规划。用 f[i] [j]表示 s 的前 i 个字符与 p 中的前 j 个字符是否能够匹配。在进行状态转移时,我们考虑 p 的第 j 个字符的匹配情况:
- 如果 p 的第 j 个字符是一个小写字母,那么我们必须在 s 中匹配一个相同的小写字母
- 如果 p 的第 j 个字符是
*,那么就表示我们可以对 p 的第 j−1个字符匹配任意自然数次 - 任意情况下,只要 p[j] 是
.,那么 p[j] 一定成功匹配 s 中的任意一个小写字母。
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
// dp[i][j]: 表示s[0, i) 与 p[0, j) 是否匹配
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true;
// 初始化第一行
for (int i = 1; i <= n; i++) {
if (i > 1 && p[i - 1] == '*' && dp[0][i - 2])
dp[0][i] = true;
}
// 状态转移
for (int i = 1; i <= m; i++) {
char cur = s[i - 1];
for (int j = 1; j <= n; j++) {
char match = p[j - 1];
if (match == '*') {
if (p[j - 2] == cur || p[j - 2] == '.') {
dp[i][j] = dp[i - 1][j];
}
if (j > 2 && !dp[i][j]) {
dp[i][j] = dp[i][j - 2];
}
} else if (match == '.') {
dp[i][j] = dp[i - 1][j - 1];
} else {
if (match == cur) {
dp[i][j] = dp[i - 1][j - 1];
}
}
}
}
return dp[m][n];
}
};
11. 盛最多水的容器
链接
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
示例 1:
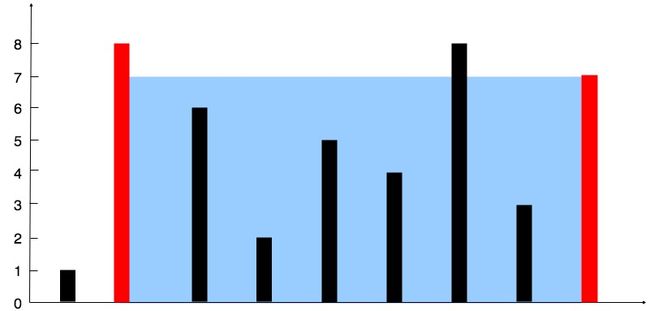
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
思路:
双指针。左右指针分别指向数组的左右两端,每次移动对应数字较小的那个指针(即此时的左指针)。容纳的水量是
两个指针指向的数字中较小值∗指针之间的距离
class Solution {
public:
int maxArea(vector<int>& height) {
int l = 0, r = height.size() - 1;
int ans = 0;
while (l < r) {
int area = min(height[l], height[r]) * (r - l);
ans = max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
};
15. 三数之和
链接
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 *a,b,c ,*使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = []
输出:[]
示例 3:
输入:nums = [0]
输出:[]
提示:
0 <= nums.length <= 3000-105 <= nums[i] <= 105
思路:
排序 + 双指针。依次枚举每个数
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
vector<vector<int>> ans;
// 枚举 a
for (int first = 0; first < n; ++first) {
// 需要和上一次枚举的数不相同
if (first > 0 && nums[first] == nums[first - 1]) {
continue;
}
// c 对应的指针初始指向数组的最右端
int third = n - 1;
int target = -nums[first];
// 枚举 b
for (int second = first + 1; second < n; ++second) {
// 需要和上一次枚举的数不相同
if (second > first + 1 && nums[second] == nums[second - 1]) {
continue;
}
// 需要保证 b 的指针在 c 的指针的左侧
while (second < third && nums[second] + nums[third] > target) {
--third;
}
// 如果指针重合,随着 b 后续的增加
// 就不会有满足 a+b+c=0 并且 b
if (second == third) {
break;
}
if (nums[second] + nums[third] == target) {
ans.push_back({nums[first], nums[second], nums[third]});
}
}
}
return ans;
}
};
17. 电话号码的字母组合
链接
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
思路:
深搜+回溯。
class Solution {
public:
vector<string> letterCombinations(string digits) {
vector<string> combinations;
if (digits.empty()) {
return combinations;
}
unordered_map<char, string> phoneMap{
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
string combination;
backtrack(combinations, phoneMap, digits, 0, combination);
return combinations;
}
void backtrack(vector<string>& combinations, const unordered_map<char, string>& phoneMap, const string& digits, int index, string& combination) {
if (index == digits.length()) {
combinations.push_back(combination);
} else {
char digit = digits[index];
const string& letters = phoneMap.at(digit);
for (const char& letter: letters) {
combination.push_back(letter);
backtrack(combinations, phoneMap, digits, index + 1, combination);
combination.pop_back();
}
}
}
};
19. 删除链表的倒数第 N 个结点
链接
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
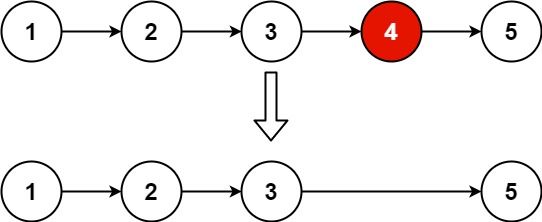
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
提示:
- 链表中结点的数目为
sz 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
进阶: 你能尝试使用一趟扫描实现吗?
思路:
- 方法一:双指针。使用两个指针 first 和 second 同时对链表进行遍历,并且 first 比 second 超前 n 个节点。当 first 遍历到链表的末尾时,second 就恰好处于倒数第 n 个节点。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummy = new ListNode(0, head);
ListNode* first = head;
ListNode* second = dummy;
for (int i = 0; i < n; ++i) {
first = first->next;
}
while (first) {
first = first->next;
second = second->next;
}
second->next = second->next->next;
ListNode* ans = dummy->next;
delete dummy;
return ans;
}
};
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
dumpy = ListNode(0, head)
fast = head
slow = dumpy
while n:
fast = fast.next
n -= 1
while fast:
slow = slow.next
fast = fast.next
slow.next = slow.next.next
return dumpy.next
-
方法二:计算链表长度。首先从头节点开始对链表进行一次遍历,得到链表的长度 L。随后我们再从头节点开始对链表进行一次遍历,当遍历到第 L−n+1 个节点时,它就是我们需要删除的节点。
class Solution { public: int getLength(ListNode* head) { int length = 0; while (head) { ++length; head = head->next; } return length; } ListNode* removeNthFromEnd(ListNode* head, int n) { ListNode* dummy = new ListNode(0, head); int length = getLength(head); ListNode* cur = dummy; for (int i = 1; i < length - n + 1; ++i) { cur = cur->next; } cur->next = cur->next->next; ListNode* ans = dummy->next; delete dummy; return ans; } }; -
方法三:栈。在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则,我们弹出栈的第 n 个节点就是需要删除的节点,并且目前栈顶的节点就是待删除节点的前驱节点。
class Solution { public: ListNode* removeNthFromEnd(ListNode* head, int n) { ListNode* dummy = new ListNode(0, head); stack<ListNode*> stk; ListNode* cur = dummy; while (cur) { stk.push(cur); cur = cur->next; } for (int i = 0; i < n; ++i) { stk.pop(); } ListNode* prev = stk.top(); prev->next = prev->next->next; ListNode* ans = dummy->next; delete dummy; return ans; } };
20. 有效的括号
链接
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
提示:
1 <= s.length <= 104s仅由括号'()[]{}'组成
思路:
栈,遇到右括号,则弹出匹配。
class Solution {
public:
bool isValid(string s) {
int n = s.size();
if (n % 2 == 1) return false;
unordered_map<char, char> map = {
{')', '('},
{']', '['},
{'}', '{'},
};
stack<char> st;
for (char c : s) {
if (map.count(c)) {
if (st.empty() || st.top() != map[c]) {
return false;
}
st.pop();
} else {
st.push(c);
}
}
return st.empty();
}
};
class Solution:
def isValid(self, s: str) -> bool:
if len(s) % 2 == 1:
return False
pairs = {
")": "(",
"]": "[",
"}": "{",
}
stack = list()
for ch in s:
if ch in pairs:
if not stack or stack[-1] != pairs[ch]:
return False
stack.pop()
else:
stack.append(ch)
return not stack
21. 合并两个有序链表
链接
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
- 两个链表的节点数目范围是
[0, 50] -100 <= Node.val <= 100l1和l2均按 非递减顺序 排列
思路:
- 方法一:递归。两个链表头部值较小的一个节点与剩下元素的
merge操作结果合并。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
if (!list2) return list1;
if (!list1) return list2;
if (list1->val < list2->val) {
list1->next = mergeTwoLists(list1->next, list2);
return list1;
} else {
list2->next = mergeTwoLists(list2->next, list1);
return list2;
}
}
};
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
if not list1:
return list2
elif not list2:
return list1
elif list1.val < list2.val:
list1.next = self.mergeTwoLists(list1.next, list2)
return list1
else:
list2.next = self.mergeTwoLists(list1, list2.next)
return list2
- 方法二:迭代。当 l1 和 l2 都不是空链表时,判断 l1 和 l2 哪一个链表的头节点的值更小,将较小值的节点添加到结果里,当一个节点被添加到结果里之后,将对应链表中的节点向后移一位。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode *ans = new ListNode(0);
ListNode *ans_ptr = ans;
while (list1 && list2) {
if (list2->val < list1->val) {
ans->next = list2;
list2 = list2->next;
} else {
ans->next = list1;
list1 = list1->next;
}
ans = ans->next;
}
ans->next = list1 ? list1 : list2;
return ans_ptr->next;
}
};
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
p = ans = ListNode(0)
while list1 and list2:
if list1.val < list2.val:
p.next = ListNode(list1.val)
list1 = list1.next
else:
p.next = ListNode(list2.val)
list2 = list2.next
p = p.next
p.next = list1 if list1 else list2
return ans.next
22. 括号生成
链接
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
提示:
1 <= n <= 8
思路:
递归+回溯。
class Solution {
public:
vector<string> generateParenthesis(int n) {
if (n == 0) return {};
// 记录所有合法的括号组合
vector<string> res;
// 回溯过程中的路径
string track;
// 可用的左括号和右括号数量初始化为 n
backtrack(n, n, track, res);
return res;
}
// 可用的左括号数量为 left 个,可用的右括号数量为 rgiht 个
void backtrack(int left, int right,
string& track, vector<string>& res) {
// 若左括号剩下的多,说明不合法
if (right < left) return;
// 数量小于 0 肯定是不合法的
if (left < 0 || right < 0) return;
// 当所有括号都恰好用完时,得到一个合法的括号组合
if (left == 0 && right == 0) {
res.push_back(track);
return;
}
// 尝试放一个左括号
track.push_back('('); // 选择
backtrack(left - 1, right, track, res);
track.pop_back(); // 撤消选择
// 尝试放一个右括号
track.push_back(')'); // 选择
backtrack(left, right - 1, track, res);
track.pop_back(); // 撤消选择
}
};
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
ans = []
def backtrack(S, left, right):
if len(S) == 2 * n:
ans.append(''.join(S))
return
if left < n:
S.append('(')
backtrack(S, left+1, right)
S.pop()
if right < left:
S.append(')')
backtrack(S, left, right+1)
S.pop()
backtrack([], 0, 0)
return ans
23. 合并K个升序链表⭐⭐
链接
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
思路:
方法一:分治合并。将 k 个链表配对并将同一对中的链表合并;第一轮合并以后, k 个链表被合并成了 k/2 个链表,平均长度为 2n/k,然后是 k/4 个链表, k/8 个链表等等;
重复这一过程,直到我们得到了最终的有序链表。
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* merge(vector <ListNode*> &lists, int l, int r) {
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
};
方法二:优先队列。按链表头节点值的大小排序,每次取最小的。
class Solution {
public:
struct Status {
int val;
ListNode *ptr;
bool operator < (const Status &rhs) const {
return val > rhs.val;
}
};
priority_queue <Status> q;
ListNode* mergeKLists(vector<ListNode*>& lists) {
for (auto node: lists) {
if (node) q.push({node->val, node});
}
ListNode head, *tail = &head;
while (!q.empty()) {
auto f = q.top(); q.pop();
tail->next = f.ptr;
tail = tail->next;
if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
}
return head.next;
}
};
31. 下一个排列⭐⭐
链接
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须** 原地 **修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
思路:
两遍扫描。注意到下一个排列总是比当前排列要大,除非该排列已经是最大的排列。
- 首先从后向前查找第一个顺序对 (i,i+1),满足a[i]
- 如果找到了顺序对,那么在区间 [i+1,n) 中从后向前查找第一个元素 j 满足 a[i]
- 交换 a[i] 与 a[j],此时可以证明区间 [i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序,而无需对该区间进行排序。
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i = nums.size() - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = nums.size() - 1;
while (j >= 0 && nums[i] >= nums[j]) {
j--;
}
swap(nums[i], nums[j]);
}
reverse(nums.begin() + i + 1, nums.end());
}
};
32. 最长有效括号⭐⭐⭐
链接
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
提示:
0 <= s.length <= 3 * 104s[i]为'('或')'
思路:
- 方法一:动态规划。我们定义 dp[i] 表示以下标 i 字符结尾的最长有效括号的长度。我们将 dp 数组全部初始化为 0 。显然有效的子串一定以 ‘)’ 结尾,因此我们可以知道以 ‘(’ 结尾的子串对应的 dp 值必定为 0 ,我们只需要求解 ‘)’ 在 dp 数组中对应位置的值。
class Solution {
public:
int longestValidParentheses(string s) {
int ans = 0, n = s.length();
vector<int> dp(n, 0);
for (int i = 1; i < n; i++) {
if (s[i] == ')') {
int last = i - dp[i - 1] - 1;
if (last >= 0 && s[last] == '(') {
dp[i] = dp[i - 1] + 2;
if (last > 0) dp[i] += dp[last - 1];
}
ans = max(ans, dp[i]);
}
}
return ans;
}
};
-
方法二:栈。
-
始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」,这样的做法主要是考虑了边界条件的处理,栈里其他元素维护左括号的下标:
- 对于遇到的每个 ‘(’ ,我们将它的下标放入栈中
- 对于遇到的每个 ‘)’ ,我们先弹出栈顶元素表示匹配了当前右括号:
- 如果栈为空,说明当前的右括号为没有被匹配的右括号,我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
- 如果栈不为空,当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
class Solution {
public:
int longestValidParentheses(string s) {
int maxans = 0;
stack<int> stk;
stk.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
stk.push(i);
} else {
stk.pop();
if (stk.empty()) {
stk.push(i);
} else {
maxans = max(maxans, i - stk.top());
}
}
}
return maxans;
}
};
- 方法三:贪心。利用两个计数器 left 和 right 。首先,我们从左到右遍历字符串,对于遇到的每个 ‘(’,我们增加 left 计数器,对于遇到的每个 ‘)’,我们增加 right计数器。每当 left 计数器与 right 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串。当 right 计数器比 left 计数器大时,我们将 left 和 right 计数器同时变回 0。
class Solution {
public:
int longestValidParentheses(string s) {
int left = 0, right = 0, maxlength = 0;
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = max(maxlength, 2 * right);
} else if (right > left) {
left = right = 0;
}
}
left = right = 0;
for (int i = (int)s.length() - 1; i >= 0; i--) {
if (s[i] == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = max(maxlength, 2 * left);
} else if (left > right) {
left = right = 0;
}
}
return maxlength;
}
};
33. 搜索旋转排序数组
链接
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000-104 <= nums[i] <= 104nums中的每个值都 独一无二- 题目数据保证
nums在预先未知的某个下标上进行了旋转 -104 <= target <= 104
思路:
二分查找。
- 如果 [l, mid - 1] 是有序数组,且 target 的大小满足 [nums[l],nums[mid]),则我们应该将搜索范围缩小至 [l, mid - 1],否则在 [mid + 1, r] 中寻找。
- 如果 [mid, r] 是有序数组,且 target 的大小满足 (nums[mid+1],nums[r]],则我们应该将搜索范围缩小至 [mid + 1, r],否则在 [l, mid - 1] 中寻找。
class Solution {
public:
int search(vector<int>& nums, int target) {
// 二分查找
int left=0;
int right=nums.size()-1;
// 这儿的条件不能是 left
while(left<=right){
int mid=(left+right)/2;
if(nums[mid]==target) return mid;
// 数组的左半部分有序;
// 注意 这儿不能是 nums[0]<=nums[mid] ,因为二分查找的子数组左右边界是会变的。
if(nums[left]<=nums[mid]){
if(target>=nums[left] && target<nums[mid]){
right=mid-1;
}else{
left=mid+1;
}
}else{ // 数组的右半部分有序;
if(target>nums[mid] && target<=nums[right]){
left=mid+1;
}else{
right=mid-1;
}
}
}
return -1;
}
};
34. 在排序数组中查找元素的第一个和最后一个位置
链接
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
思路:
二分查找。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int l = findL(nums, target);
int r = findR(nums, target);
vector<int> ans;
ans.push_back(l);
ans.push_back(r);
return ans;
}
int findR(vector<int> & s, int target) {
int ans = -1;
int l = 0, r = s.size() - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (s[mid] > target) {
r = mid - 1;
} else if (s[mid] <= target) {
if (s[mid] == target) ans = mid;
l = mid + 1;
}
}
return ans;
}
int findL(vector<int> & s, int target) {
int ans = -1;
int l = 0, r = s.size() - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (s[mid] >= target) {
if (s[mid] == target) ans = mid;
r = mid - 1;
} else if (s[mid] < target) {
l = mid + 1;
}
}
return ans;
}
};
39. 组合总和
链接
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 301 <= candidates[i] <= 200candidate中的每个元素都 互不相同1 <= target <= 500
思路:
深度优先遍历+回溯。
class Solution {
public:
void dfs(vector<int>& candidates, int target, vector<vector<int>>& ans, vector<int>& combine, int idx) {
// 越界
if (idx == candidates.size()) {
return;
}
// 找到了
if (target == 0) {
ans.emplace_back(combine);
return;
}
// 不选当前数,直接跳过
dfs(candidates, target, ans, combine, idx + 1);
// 选择当前数
if (target - candidates[idx] >= 0) {
combine.emplace_back(candidates[idx]);
dfs(candidates, target - candidates[idx], ans, combine, idx);
combine.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans; // 保存最终结果
vector<int> combine; // 保存当前结果
dfs(candidates, target, ans, combine, 0); // 深搜
return ans;
}
};
42. 接雨水⭐⭐
链接
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
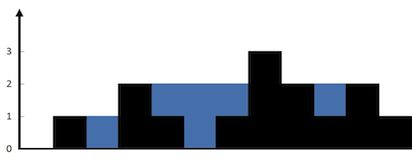
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
思路:
- 方法一:动态规划.
- 对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 ii 处的水能到达的最大高度减去height[i]。
class Solution {
public:
int trap(vector<int>& height) {
// 找到当前位置左边最大高度和右边最大高度
int n = height.size();
vector<int> left(n), right(n);
for (int i = 1; i < n; i++) {
left[i] = max(left[i-1], height[i-1]);
right[n-i-1] = max(right[n-i], height[n-i]);
}
int ans = 0;
for (int i = 0; i < n; i++) {
int mi = min(left[i], right[i]);
if (mi > height[i]) {
ans += mi - height[i];
}
}
return ans;
}
};
- 方法二:单调栈。可以用单调栈计算能接的雨水总量。维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组 height 中的元素递减。
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0;
stack<int> stk;
int n = height.size();
for (int i = 0; i < n; ++i) {
while (!stk.empty() && height[i] > height[stk.top()]) {
int top = stk.top();
stk.pop();
if (stk.empty()) {
break;
}
int left = stk.top();
int currWidth = i - left - 1;
int currHeight = min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stk.push(i);
}
return ans;
}
};
- 方法三:双指针
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0;
int left = 0, right = height.size() - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
};