二叉树的基本操作

一、二叉树的定义与基本术语
（一）基本概念
二叉树是n（n≥0）个结点的有限集合：
① 或者为空二叉树，即n = 0。
② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
特点：①每个结点至多只有两棵子树 ②左右子树不能颠倒（二叉树是有序树）【注意区别：度为2的有序树】

算法思想：二叉树使用链表来定义，指针域为两个，分别指向左子树和右子树的跟结点地址。二叉树的创建根据先序遍历的思想，空的左子树或右子树结点用“.”来表示。

树的销毁需要利用后序遍历，逐级销毁左子树、右子树、根节点，如果按照先序和后序的话，那么根节点销毁后会找不到其左或右子树。

求树的高度，利用递归算法，计算左右子树的高度，取上述两者的最大值加1，即为二叉树在根节点处的高度。

求左右孩子比较简单，求双亲则需要将这个树重新遍历，如果某个结点的左或右子树结点等于要查找的节点，则输出该节点。

树的先序遍历，中序遍历和后序遍历都是使用递归的思想来实现的，只不过访问左子树、根节点和右子树的顺序不同，而层次遍历则利用队列来完成，即每一个根节点出队，都会使得它的左孩子和右孩子入队。

#include
#include
using namespace std;
typedef char ElemType;
typedef int Status;
//二叉树的二叉链表存储表示
typedef struct BiTNode{
	ElemType data; //数据元素 
	struct BiTNode *lchild,*rchild;//左右孩子指针 
}BiTNode,*BiTree; 
Status InitBiTree(BiTree T);         //初始化树 1
BiTree DestroyBiTree(BiTree &T);      //销毁树  注意：销毁树只能用后序遍历的方法进行销毁2
void ClearBiTree(BiTree &T);         //清空树 3
void BiTreeEmpty(BiTree T);          //判空 4
int BiTreeDepth(BiTree T);           //求树的深度 5
void Root(BiTree T,ElemType &e);     //求根 6
BiTree FindNode(BiTree T,ElemType x);//查找 7
void Parent(BiTree T,BiTNode* cur_p,BiTNode* &parent);//cur_p结点的求双亲，并用parent来记录8
BiTree LeftChild(BiTree T,BiTNode* cur_p,BiTNode* &leftchild);//求cur_p结点的左孩子 9
BiTree RightChild(BiTree T,BiTNode* cur_p,BiTNode* &rightchild);//求cur_p结点的右孩子10
BiTNode* LeftBrother(BiTree T,BiTNode* cur_p,BiTNode* &leftbrother);//求cur_p结点的左兄弟11
BiTNode* RightBrother(BiTree T,BiTNode* cur_p,BiTNode* &rightbrother);//求cur_p结点的右兄弟12
void Assign(BiTree &T,BiTNode* cur_p,ElemType value);  //赋值13
void InsertChild(BiTree &T,BiTNode* cur_p,int LR,BiTree &C); //插入 14
void DeleteChild(BiTree &T,BiTNode* cur_p,int LR);  //删除 15
void findparent(BiTree T,BiTNode* cur_p,BiTNode* &parent);  //求双亲的辅助函数16
void CreateBiTree(BiTree &T);        //利用先序遍历创建树 17
Status PreOrderTraverse(BiTree T);   //先序遍历rLR 18
void InOrderTraverse(BiTree T);      //中序遍历LrR19
void PostOrderTraverse(BiTree T);    //后序遍历LRr 20
void LevelOrderTraverse(BiTree T);   //层次遍历 21
int main()
{
	BiTree T;
	InitBiTree(T);
	cout<<"输入创建树的先序序列：";
	CreateBiTree(T);
	cout<<"先序遍历：";
	PreOrderTraverse(T);
	cout<>x;
	BiTree T1=FindNode(T,x);
	cout<<"元素为："<data<data<data<data<lchild=NULL;
	T->rchild=NULL;
	return 1;
}
void CreateBiTree(BiTree &T)
{
	char c;
	cin>>c;
	if (c == '.')
		T = NULL;
	else {
		T = (BiTree)malloc(sizeof(BiTNode));     //例如ABD.G...CE..F..
		T->data = c;
		CreateBiTree(T->lchild);
		CreateBiTree(T->rchild);
	}
}
Status PreOrderTraverse(BiTree T)  //先序遍历rLR 
{
	if(!T)
	    return 0;
	printf("%c ",T->data);
	PreOrderTraverse(T->lchild);  
	PreOrderTraverse(T->rchild);
	return 1;
}
void InOrderTraverse(BiTree T)    //中序遍历LrR
{
	if(T!=NULL)
	{
		InOrderTraverse(T->lchild);  //中序遍历左子树 
		cout<data<<" ";               //访问根节点 
		InOrderTraverse(T->rchild);  //中序遍历右子树 
	}
}
void PostOrderTraverse(BiTree T) //后序遍历LRr 
{
	if(T!=NULL)
	{
		PostOrderTraverse(T->lchild);  //后序遍历左子树 
		PostOrderTraverse(T->rchild);  //后序遍历右子树
		cout<data<<" ";          //访问根节点 
		   
	}
}/*
BiTree DestroyBiTree(BiTree &T)  //销毁树
{
	if(T)
	{
		T->lchild=DestroyBiTree(T->lchild);  //销毁左子树          
		T->rchild=DestroyBiTree(T->rchild);  //销毁右子树 
		free(T);                             //销毁根节点
		return NULL;
	}
} */
BiTree DestroyBiTree(BiTree &T)  //销毁树
{
	if (T->lchild)
		DestroyBiTree(T->lchild);
	if (T->rchild)
		DestroyBiTree(T->rchild);
	T = NULL;
	free(T);
} 
void ClearBiTree(BiTree &T)  //清空树 
{
	T->lchild=NULL;
	T->rchild=NULL;
} 
void BiTreeEmpty(BiTree T)   //判空 
{
	if(T->lchild==NULL&&T->rchild==NULL)
	cout<<"此树为空"<lchild);
		rigthdepth=BiTreeDepth(T->rchild);
		return (leftdepth>rigthdepth) ? (leftdepth+1) : (rigthdepth+1);
	 } 
} 
void Root(BiTree T,ElemType &e)  //求根
{
	e=T->data;
}
BiTree FindNode(BiTree T,ElemType x) //查找
{ 
	BiTree p=NULL;
	if(T==NULL) return NULL;
	else if(T->data==x) return T;
	else
	{
		p=FindNode(T->lchild,x);
		if(p==NULL)
		return FindNode(T->rchild,x);
		else
		return p;
	}
}
void findparent(BiTree T,BiTNode* cur_p,BiTNode* &parent)  //辅助函数 
{
	if (!T->lchild && !T->rchild)
		return;
	else {
		if (T->lchild == cur_p || T->rchild == cur_p)
			parent = T;
		else if (T->lchild)
			findparent(T->lchild, cur_p, parent);
		if (T->rchild)
			findparent(T->rchild, cur_p, parent);
	}
}
void Parent(BiTree T, BiTNode* cur_p, BiTNode* &parent)  //求双亲
{
	parent = NULL;
	if (T == cur_p)
		return;
	else
		findparent(T, cur_p, parent);
}
BiTree LeftChild(BiTree T,BiTNode* cur_p,BiTNode* &leftchild) //求cur_p结点的左孩子 
{
	if(!cur_p->lchild)
	leftchild=NULL;
	else
	leftchild=cur_p->lchild;
} 
BiTree RightChild(BiTree T,BiTNode* cur_p,BiTNode* &rightchild)//求cur_p结点的右孩子
{
	if(!cur_p->rchild)
	rightchild=NULL;
	else
	rightchild=cur_p->rchild;
}
BiTNode* LeftBrother(BiTree T,BiTNode* cur_p,BiTNode* &leftbrother) //求cur_p结点的左兄弟
{
	BiTNode *parent;
	Parent(T, cur_p,parent);
	if(!parent)
	leftbrother=NULL;
	else if(cur_p==parent->lchild)
	leftbrother=NULL;
	else
	leftbrother=parent->lchild;
}//ABD.G...CE..F..
BiTNode* RightBrother(BiTree T,BiTNode* cur_p,BiTNode* &rightbrother)//求cur_p结点的右兄弟
{
	BiTNode *parent;
	Parent(T, cur_p,parent);
	if(!parent)
	rightbrother=NULL;
	else if(cur_p==parent->rchild)
	rightbrother=NULL;
	else
	rightbrother=parent->rchild;
}
void Assign(BiTree &T,BiTNode* cur_p,ElemType value)  //赋值 
{
	cur_p->data=value; 
} 
void InsertChild(BiTree &T,BiTNode* cur_p,int LR,BiTree &C) //插入
{
  if(LR==0)
  {
  	cur_p->lchild=C; 
  }
  if(LR==1)
  {
  	cur_p->rchild=C;
  }
}
void DeleteChild(BiTree &T,BiTNode* cur_p,int LR)  //删除
{
	if(LR==0)
  {
  	 DestroyBiTree(cur_p->lchild);
  	 cur_p->lchild=NULL;
  }
  if(LR==1)
  {
  	DestroyBiTree(cur_p->rchild);
  	cur_p->rchild=NULL;
  }
}   
void LevelOrderTraverse(BiTree T)     //层次遍历
{
	int i = 0, j = 0;
	BiTree n[100];
	n[j++] = T;
	while (i != j) {
		printf("%c ", n[i]->data);
		if (n[i]->lchild)
			n[j++] = n[i]->lchild;
		if (n[i]->rchild)
			n[j++] = n[i]->rchild;
		i++;
	}
}

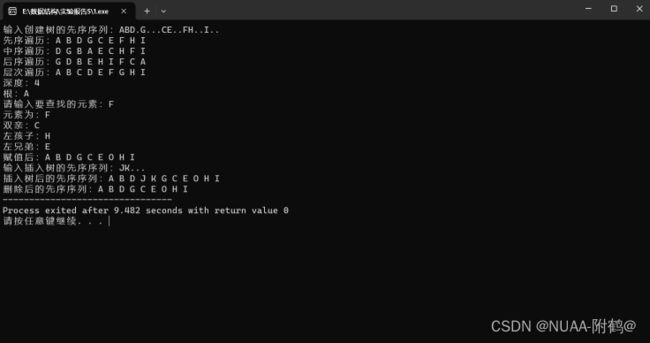
运行结果