leetcode 逃离大迷宫

题目链接
思路：数学+深搜
分析：在一个巨大的网格中，只有一部分障碍阻挡，是否能从一个点到另一个点，首先可以知道，这个巨大的网格中总的格子数相比于障碍是远大于的关系，而且，这个题目网格数是10⁶ *10⁶首先不可能单纯的深搜，因为格子数太多了。
这里障碍的个数，最多两百，那么可以从这里着手，首先，从一个点到另一个点，只有一个条件。
两个点是否有任何一个被障碍围住，如果有，则不可能到达，如果没有，则可到达。
那么现在的问题在于，如何判定一个点是否被障碍围住？

方案一：
现在的问题有点类似于给你一个200米的篱笆，在一个有四面墙的长为10⁶正方形中围出的最大面积。
但是不同的是，这里给的是200个格子，，四面墙的长度为10⁶的格子。求的是能围出来的图形，包含格子最多的是多少个。
其实最大的就是一个等腰直角三角形，斜边是200个格子。
举例：先来一个4*4的格子，给你4个格子，能围住的最多的格子数。

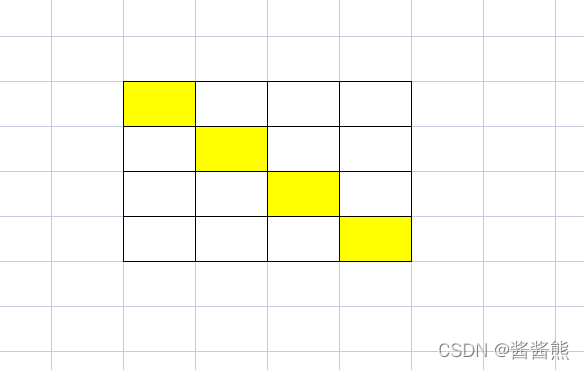
那么能围住的就是一半，如果想多围住一个格子，那么需要这样。

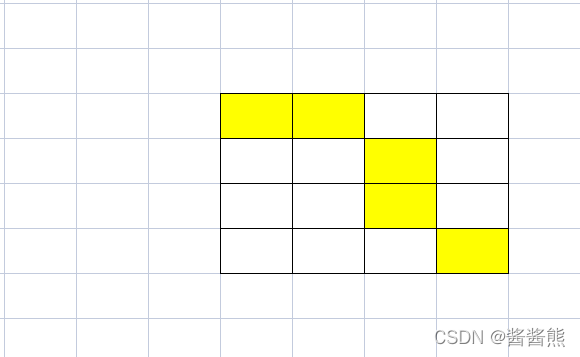
这样就需要多消耗两个格子，那么如果不是4*4，而是无限大呢，给你5个格子，能围住多少个

这就是围住的最多的，
然后这个题中是最多200个格子，
能围住的也就是199 + 198 + 197 +……+1也就是19900个格子。

那么 在一个几乎无限大的网格中，200个格子最大能围住19900个格子。

那么，也就是说，如果从任何一个点出发，如果能走过的格子数超过了19900个格子，那么肯定没被围住。
代码：

class Solution {

    int[][] forwarding = {
            {0,1},//右移
            {1,0},//下移
            {0,-1},//左移
            {-1,0}//上移
    };

    public boolean isEscapePossible(int[][] blocked, int[] source, int[] target) {
		//如果一共就1个阻碍的格子，那肯定围不住
        if(blocked.length<2){
            return true;
        }
		
		//用来记录阻碍的格子，为了加速查找下一个格子是不是阻碍
        HashSet<Long> blockedSet = new HashSet<>();

        for(int[] block : blocked){
        	//用一个long型来标识两个int型
            blockedSet.add(block[0] * 1000000L + block[1]);
        }
        //分别从source 和target开始走，看能不能走出超过19900个格子
        return dfs(blockedSet, source, new HashSet<>(), target) && dfs(blockedSet, target, new HashSet<>(), source);
    }

	//深搜走格子，看是否能超过19900个格子
    private boolean dfs(Set<Long> set, int[] cur, Set<Long> visited, int[] tar){
    	//如果此时已经到了目的地了，那么不管是不是超过19900个格子，不用走了，已经到了
        if(cur[0]== tar[0] && cur[1] == tar[1]){
            return true;
        }
        //如果超过了19900个格子，说明肯定没被围住，上面已经讲过了
        if( visited.size() >19900 ){
            return true;
        }

		//计算当前格子下标的值，也是为了用long型表示两个int型，这样也是为了加速查找是否已经找过
        Long hash = cur[0] * 1000000L + cur[1];
        //加入已经走过的格子
        visited.add(hash);
		
		//四个方向dfs
        for(int[] f : forwarding){
        	//下一个格子的下标
            int[] next = {cur[0] + f[0], cur[1] + f[1]};
            //计算下一个格子的hash
            hash = next[0] * 1000000L + next[1];
            //如果越界或下一个是阻碍的格子或下一个格子已经走过，那么不用走了
            if(next[0] < 0 || next[1] < 0 || next[0]>=1000000 || next[1]>=1000000 || set.contains(hash) || visited.contains(hash)){
                continue;
            }
            //否则进入下一个格子
            if(dfs(set,next,visited, tar)){
                return true;
            }
        }
        return false;
    }
}

缺点：要走到19900这么多格子才能判定他没被围住，复杂度较高。

方案二： 我们想想，最多两百个格子在能围住的最大的图形中，能放进去的最大的一条线段能有多长？
也就是说，200个格子，最多能围住多长的线段。

先小点，5个格子，能围住最长的线段多长。

答案是4个。
那么200个格子，最长能围住199个格子。

那么上面的代码可以改为这样。
代码：

class Solution {

    int[][] forwarding = {
            {0,1},//右移
            {1,0},//下移
            {0,-1},//左移
            {-1,0}//上移
    };

    public boolean isEscapePossible(int[][] blocked, int[] source, int[] target) {
		//如果一共就1个阻碍的格子，那肯定围不住
        if(blocked.length<2){
            return true;
        }
		
		//用来记录阻碍的格子，为了加速查找下一个格子是不是阻碍
        HashSet<Long> blockedSet = new HashSet<>();

        for(int[] block : blocked){
        	//用一个long型来标识两个int型
            blockedSet.add(block[0] * 1000000L + block[1]);
        }
        //分别从source 和target开始走，看能不能走出超过19900个格子
        return dfs(blockedSet, source, new HashSet<>(),source, target) && dfs(blockedSet, target, new HashSet<>(),target, source);
    }

	//深搜走格子，看最长的线段是否能超过199个格子
    private boolean dfs(Set<Long> set, int[] cur, Set<Long> visited,int[] source, int[] tar){
    	//如果此时已经到了目的地了，那么不管是不是超过199个格子，不用走了，已经到了
        if(cur[0]== tar[0] && cur[1] == tar[1]){
            return true;
        }
        //如果围住的超过199个格子，说明肯定没被围住，上面已经讲过了
        if( Math.abs(cur[0]-source[0])+Math.abs(cur[1]-source[1]) >= 199 ){//曼哈顿举例
            return true;
        }

		//计算当前格子下标的值，也是为了用long型表示两个int型，这样也是为了加速查找是否已经找过
        Long hash = cur[0] * 1000000L + cur[1];
        //加入已经走过的格子
        visited.add(hash);
		
		//四个方向dfs
        for(int[] f : forwarding){
        	//下一个格子的下标
            int[] next = {cur[0] + f[0], cur[1] + f[1]};
            //计算下一个格子的hash
            hash = next[0] * 1000000L + next[1];
            //如果越界或下一个是阻碍的格子或下一个格子已经走过，那么不用走了
            if(next[0] < 0 || next[1] < 0 || next[0]>=1000000 || next[1]>=1000000 || set.contains(hash) || visited.contains(hash)){
                continue;
            }
            //否则进入下一个格子
            if(dfs(set,next,visited,source,tar)){
                return true;
            }
        }
        return false;
    }
}

也就是说，超过了199个格子形成了线段，200个格子是无法将其围住的。

注意这里计算的举例是曼哈顿举例。
因为每次只能上下左右四个方向走，不能斜着走，所以每次计算的不是直线举例，而是曼哈顿距离。

好好生活。
不打扰是我的温柔。