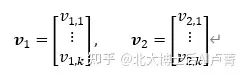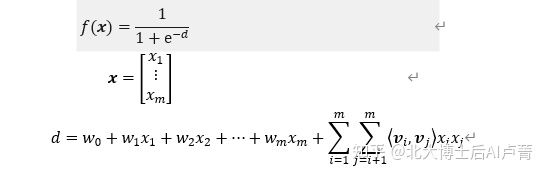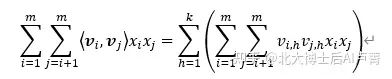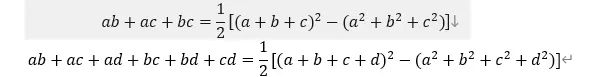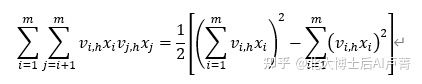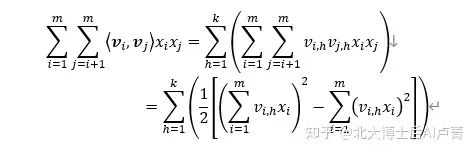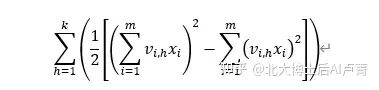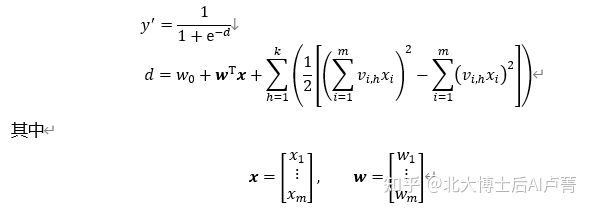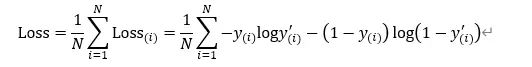《速通机器学习》-因子分解模型

（由于平台稿件格式问题，公式格式不能正确写上；如若读写困难可后台私信我要完整电子版）

4.1　基本原理和特征交叉

4.1.1　基本原理

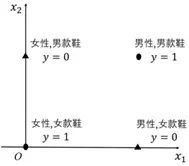
逻辑回归简单实用，没有复杂的数值运算，非常适合在对性能要求较高的场景中进行在线预测，目前已经成为企业应用的标配和基线。但是，随着互联网的发展，以及应用场景的日益复杂，人们对机器学习的期待日渐提高，在一些复杂的场景中，逻辑回归显得有些力不从心。例如，在电商推荐场景中预测用户是否会购买某商品，商品和用户都将作为模型特征，购买行为的发生与否将作为预测类别。输入为 x=〖[x_1,x_2]〗^T，x_1=0 表示女性，x_1=1 表示男性，x_2=0 表示女鞋，x_2=1 表示男鞋，输出 y 表示用户的购买概率，特征分布如图4-1所示。

图4-1

其中，椭圆形表示用户会购买（y=1），三角形表示用户不会购买（y=0）。可以看出，这是一个典型的异或问题（在需要判断二者是否匹配的分类场景中，这种问题广泛存在）。通过前面的学习我们知道，要想用逻辑回归解决异或问题，就要对特征进行升维。特征交叉是一个非常好用的特征升维方法。例如，将 x=〖[x_1,x_2]〗^T 升维至 x=〖[x_1,x_2,x_1 x_2]〗^T，就可以解决异或问题。

然而，在真实的场景中，直接使用特征交叉会面临以下困难。

一般来说，特征维度有成千上万维，如果人工进行特征交叉，是不太容易把所有需要的交叉特征都找出来的，并且很多交叉特征并不是我们能想象出来的。因此，只能以穷举的方式对所有的特征进行两两交叉。例如，6维特征的交叉特征有 C_6^2=15 维。再如，在实际场景中并不算高的1000维特征，有 C_1000^2=499500 维的交叉特征。如此规模的特征，会给存储和计算带来沉重的负担并造成维数灾难（将在5.4节介绍）。

对于交叉后的高维特征，很多交叉特征非常稀疏，甚至在训练集里从未出现过（例如交叉项 x_i x_j=0、x_j=1 和 x_j=1 在训练样本中从未同时出现）。这时，特征所对应的系数 w_(i,j) 在使用梯度下降法时不会更新，w_(i,j) 永远都是一开始的随机值。但是，一旦在真实的生产环境中上线使用，只要有交叉特征出现（x_i x_j=1），w_(i,j) x_i x_j=w_(i,j) 就是一个随机数，相当于给模型注入了噪声。

待学习的特征系数 w_(i,j) 有上百万个。在机器学习领域，需要学习的参数越多，往往就会要求越多的数据。训练百万参数所需的样本是很难获得的，且如此高的维度几乎注定导致维数灾难。目前，参数数量和训练样本数量的对应关系是一个研究热点，尚无定论，但二者成正相关是毋庸置疑的。

很多特征本身具有一定的相似性。假设用户对商品的颜色“大红色”和“桃红色”的喜好没有差别或差别较小。如果在训练样本中“女鞋”（x_i）和“大红色”（x_j）的组合经常出现，那么 w_(i,j) 将多次得到训练，结果也相对准确。如果“女鞋”（x_i）和“桃红色”（x_p）的组合没有出现过，那么 w_(i,p) 将不会得到更新，一直是刚开始的随机值。因此，只要样本中出现“女鞋”和“桃红色”的组合，就很难得到准确的预测结果。其实，完全可以借鉴“女鞋”和“大红色”这个特征所对应的 w_(i,j)，将其作为 w_(i,p) 的近似特征。但很遗憾，直接对特征进行交叉无法实现这一点。

因为上述缺点，在实际应用中很少直接进行特征交叉，通常会采用间接交叉的方式。以特征 x_1 和 x_2 为例，间接交叉会将 x_1 x_2 的系数 w_1,2 解耦，拆解成向量 v_1 和 v_2，向量维度为 k，即

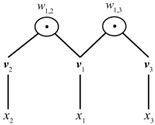
拆解向量后，v_1 只和特征 x_1 有关，v_2 只和特征 x_2 有关。此时，系数 w_1,2=〈〖v_i,v〗_j 〉。〈〖v_i,v〗_j 〉 表示 v_1 和 v_2 的向量内积，用于衡量两个向量之间的相似度（不熟悉内积的读者可以参考本书第1章）。同理，在计算 x_1,2 的系数 w_1,3 时，可以解耦成 v_1 和 v_3，v_3 和特征 x_3 有关。这样，组合特征系数 w_1,2 和 w_1,3 就不是完全独立的了，它们都会受 v_1 的影响。上述分析如图4-2所示。

图4-2

因此，逻辑回归将被改造成以下模型。

〖w_0+w〗_1 x_1+w_2 x_2+⋯+w_m x_m 和标准逻辑回归并无二致。∑_(i=1)^m▒∑_(j=i+1)^m▒〖〈〖v_i,v〗_j 〉 x_i x_j 〗 为交叉

特征项，通过拆解 w_(i,j)=〈〖v_i,v〗_j 〉 来表达特征交叉，覆盖了所有的特征两两配对。上述模型

称为因子分解机（Factorization Machine，FM）。“Factorization”的意思是分解，意味着对 w_(i,j) 的拆解。那么，因子分解模型有哪些优点呢?

假设一共有 m 维特征。如果直接两两交叉，那么一共有 C_m^2=(m(m-1))/2 个待学习参数。如果使用系数解耦的方法，每个特征对应于一个 k 维向量 v，那么待学习参数有 m×k 个。k 的值一般都不大——k=100 已经足够大了。显然 mk≪(m(m-1))/2，待学习参数的数量大幅减少了。参数的数量减少后，对训练样本数量的要求就降低了，同时，使用的存储空间减少了。

特征之间的相似度都可以用 v 来表示。如果 x_1 和 x_2 分别对应于特征“大红色”和“桃红色”，那么它们所对应的向量内积 〈〖v_i,v〗_j 〉 会比较大。这反映了特征的相似性。相似的特征表明，它们在特征组合中所起的作用类似。

在训练样本中，如果交叉项 x_i x_j 从未出现，但 x_i、x_j 分别和其他特征的组合在样本中经常出现，那么 v_i 和 v_j 也能得到充分的训练。在实际使用时，即使碰到训练集中未出现过的交叉特征 x_i x_j，也能计算出靠谱的 w_(i,j)=〈〖v_i,v〗_j 〉。

4.1.2　特征交叉简化

尽管交叉项 ∑_(i=1)^m▒∑_(j=i+1)^m▒〖〈〖v_i,v〗_j 〉 x_i x_j 〗 巧妙地解决了特征两两交叉时产生的系数过多的

问题，但没有解决运算量过大的问题。∑_(i=1)^m▒∑_(j=i+1)^m▒〖〈〖v_i,v〗_j 〉 x_j 〗 的运算量为 O(km^2)。如果运

算量过大，在进行在线预测时，就会给机器造成很大的性能压力。因此，需要对其进行化简。

首先，从 〈〖v_i,v〗_j 〉=∑_(h=1)^k▒〖v_(i,h) v_(j,h) 〗 中可以看出，在计算内积时，只有处于同一维度的特

征才会相乘，因此，可以进行第一次化简，公式如下。

下面讨论一下在维度 h 下 ∑_(i=1)^m▒∑_(j=i+1)^m▒〖v_(i,h) v_(j,h) x_i x_j 〗 如何化简。复习中学阶段学过的一

组数学公式，具体如下。

依此类推，有

可以在维度 h 下得到

那么，在所有的维度上，最终结果为

其中

所对应的运算量为 O(km)。通过对模型的化简，运算量从 O(km^2) 降至 O(km)。所以，最终的模型为

w_0+w^T x 对应于逻辑回归，∑_(h=1)^k▒(1/2 [(∑_(i=1)^m▒〖v_(i,h) x_i 〗)^2-∑_(i=1)^m▒(v_(i,h) x_i )^2 ]) 对应于新增的特征

交叉项。

4.1.3　参数学习

作为逻辑回归的改进版本，因子分解模型仅在特征处巧妙地使用向量 v 进行了特征的两两交叉，并把参数的增量控制在可以接受的范围内。在模型训练阶段，因子分解模型仍使用梯度下降法。

因子分解模型是一个二分类模型，其损失函数使用模型输出和样本标签之间的KL距离进行计算，即

模型的待求参数为 w 和 v_(j,h)，它们分别对应于逻辑回归的参数和交叉项的参数。

上述求导过程和逻辑回归并无二致。

4.2　因子分解模型和矩阵分解

熟悉推荐系统的读者都知道，用户的点击行为可以构成一个行为矩阵。该矩阵的行表示用户（User），列可以表示视频、新闻、商品等（通常称为Item）。假设一共有 N 个User和 M 个Item，矩阵的维度是 N×M，矩阵中的元素表示用户对商品的喜欢程度（1为喜欢，0为不喜欢）。这里的“喜欢”通常是根据具体的产品形态定义的，例如在短视频场景中涉及观看完成度、是否收藏等，在电商场景中涉及购买与否、评价星级等。

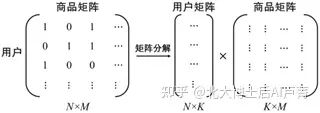
在推荐系统中有一个经典的方法，就是将行为矩阵分解成两个矩阵相乘的形式，例如用户矩阵和商品矩阵（具体的分解方法涉及很多数学知识，本书不再赘述）。其中，用户矩阵的维度为 N×K，商品矩阵的维度为 K×M，如图4-3所示。

图4-3

在用户矩阵中，每一行代表一个用户 u_i，它是一个 K 维向量（这个向量是用户的隐含表示）。在商品矩阵中，每一列对应于一个商品 v_j，每个商品也对应于一个 K 维向量。通过对用户向量和商品向量计算内积 〈〖u_i,v〗_j 〉，就可以表示用户对商品的喜欢程度，达到预测的目的。

矩阵分解在理论上是可行的，但实际的应用并不多，其原因在于计算量巨大。例如，有2000万个用户、200万个商品，那么矩阵中就有40万亿个元素——很难分解。在构建行为矩阵时：如果用户明确表示喜欢（例如愿意购买、观看等），就将相应的元素置1；如果用户明确表示不喜欢（例如给差评、打低分），就将相应的元素置0。然而，大部分商品是用户没有接触过的，何谈“爱恨”？矩阵分解的想法固然美好，但仍有缺陷。

我们回头看一下因子分解模型。在使用FM预测用户对商品的喜欢程度的场景中，采用one-hot方式对用户和商品进行编码（输入特征），N 个用户对应于 N 维向量，M 个商品对应于 M 维向量，因此，特征总维度为 M+N。每次训练 M+N 维特征时，有且仅有两个元素（用户 x_i，商品 x_j）为1，其他元素都为0。省略所有为0的特征，因子分解模型的核心部分为

d=w_i x_i+w_j x_j+〈〖u_i,v〗_j 〉 x_i x_j

u_i 为用户所对应的向量，v_j 为商品所对应的向量，内积 〈〖u_i,v〗_j 〉 就是用户和商品的相似度，这和通过矩阵分解进行预测的方式一模一样。可以看出，因子分解模型包括矩阵分解，或者说，矩阵分解是因子分解模型的特例（不考虑线性部分 w_i x_i）。

与矩阵分解相比，因子分解模型是一个更为宏大的框架，在特征层面可以引入更多维度（例如年龄、价格等）的特征来获得特征相似度，而矩阵分解只支持两类特征（用户、商品）。在训练样本的构建上，因子分解模型也没有矩阵分解不知道如何对未见过的部分进行赋值的问题。

---

对机器学习感兴趣的读者可以去主页关注我；本人著有《速通深度学习》以及《速通机器学习数学基础》二书，想要完整版电子档可以后台私信我；想一起学习机器学习的话也可以后台私信，本人所做机器学习0基础教程已有60余章还未公开；想了解的话也是后台私信或者评论区留言。