MATLAB环境下一种贝叶斯稀疏盲反卷积算法

稀疏盲反卷积贝叶斯估计方法通常使用伯努利-高斯分布(BG)先验的稀疏序列建模，并利用马尔可夫链蒙特卡罗(MCMC)方法进行未知估计。然而，BG模型的离散性会有计算瓶颈。为了解决这个问题，提出一个替代方案，采用MCMC方法对稀疏序列进行建模（使用正反伽马先验）。除了稀疏性，还考虑了时间以及卷积序列的频域约束，通过广泛的模拟和表征计算增益相对于利用BG建模的现有方法证明了提出方法的有效性。

clear all;
close all;
addpath(strcat(pwd,'\solvers'));
addpath(strcat(pwd,'\datasets'))
% change file_name to the '.mat' file containing the data
file_name = strcat(pwd,'\datasets\mendel_sequence_data');
% load data | this function must be updated/changed according to the 
% structure of the input data file
data = get_data(file_name);
% get parameters
params = get_params(data);
% run the sampler and get the samples from the posterior distribution
[samples,diagnostics] = run_MCMC(data,params);
% get estimates from the samples
MMSE_estimates = get_estimates(samples,params);
% correct time-shift and scaling ambiguities to match the true sequences
if isfield(data,'x_true') && isfield(data,'h_true')
    [MMSE_estimates_corrected,samples_corrected] = correct_shift_and_scale(MMSE_estimates,samples,data,params);
    
    figure;plot(data.x_true);hold on;grid on;plot(MMSE_estimates_corrected.x);
    xlabel('n');ylabel('Amplitude');legend('True Sequence','Recovered Sequence');
    title('Recovered Sparse Sequence');

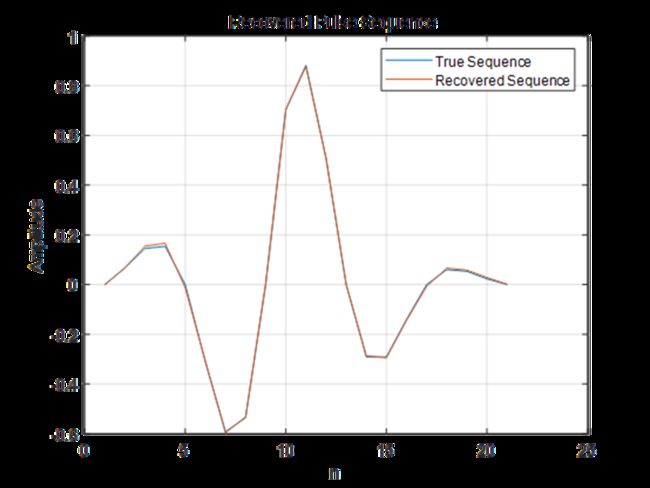
    figure;plot(data.h_true);hold on;grid on;plot(MMSE_estimates_corrected.h);
    xlabel('n');ylabel('Amplitude');legend('True Sequence','Recovered Sequence');
    title('Recovered Pulse Sequence');
else
    figure;plot(MMSE_estimates.x);grid on;
    xlabel('n');ylabel('Amplitude');title('Recovered Sparse Sequence');

    figure;plot(MMSE_estimates.h);grid on;
    xlabel('n');ylabel('Amplitude');title('Recovered Pulse Sequence');
end

function [MMSE_estimates] = get_estimates(samples,params)
    burn_in_ratio = params.burn_in_ratio;
    discarded_samples = burn_in_ratio*params.num_of_MCMC_iteration;
    
    if params.solver == "NIGS1" || params.solver == "NIGS2"
        MMSE_estimates.x = mean(samples.x(:,discarded_samples:end),2);
        MMSE_estimates.h = mean(samples.h(:,discarded_samples:end),2);
        MMSE_estimates.lambda_x = mean(samples.lambda_x(:,discarded_samples:end),2);
        MMSE_estimates.lambda_v = mean(samples.lambda_v(:,discarded_samples:end),2);
    else
        MMSE_estimates.x = mean(samples.x(:,discarded_samples:end),2);
        MMSE_estimates.h = mean(samples.h(:,discarded_samples:end),2);
        MMSE_estimates.s = mean(samples.s(:,discarded_samples:end),2);
        MMSE_estimates.lambda_v = mean(samples.lambda_v(:,discarded_samples:end),2);
    end
end

function [MMSE_estimates_corrected,samples_corrected] = correct_shift_and_scale(MMSE_estimates,samples,data,params)
    h_true = data.h_true;
    
    h_est = MMSE_estimates.h;
    x_est = MMSE_estimates.x;
    if params.solver == "NIGS1" || params.solver == "NIGS2"
        lambda_x_est = MMSE_estimates.lambda_x;
    else
        s_est = MMSE_estimates.s;
    end
    lambda_v_est = MMSE_estimates.lambda_v;
    T = length(h_est);
    
    delay_array = -round(T/2):round(T/2);
    error = zeros(length(delay_array),1);
    alpha = zeros(length(delay_array),1);
    for n = 1:length(delay_array)
        h_shifted = circshift(h_est,delay_array(n));
        alpha(n) = (h_shifted'*h_true)/(h_shifted'*h_shifted);
        h_shifted_scaled = alpha(n)*h_shifted;
        error(n) = sum(abs(h_shifted_scaled - h_true).^2);
    end
    [~,min_idx] = min(error);
    MMSE_estimates_corrected.h = circshift(h_est,delay_array(min_idx))*alpha(min_idx);
    MMSE_estimates_corrected.x = circshift(x_est,-delay_array(min_idx))/alpha(min_idx);
    if params.solver == "NIGS1" || params.solver == "NIGS2"
        MMSE_estimates_corrected.lambda_x = circshift(lambda_x_est,-delay_array(min_idx),1)*(alpha(min_idx)^2);
    else
        MMSE_estimates_corrected.s = circshift(s_est,-delay_array(min_idx),1)*(alpha(min_idx)^2);
    end
    MMSE_estimates_corrected.lambda_v = lambda_v_est;
    
    samples_corrected.h = circshift(samples.h,delay_array(min_idx))*alpha(min_idx);
    samples_corrected.x = circshift(samples.x,-delay_array(min_idx))/alpha(min_idx);
    if params.solver == "NIGS1" || params.solver == "NIGS2"
        samples_corrected.lambda_x = circshift(samples.lambda_x,-delay_array(min_idx),1)*(alpha(min_idx)^2);
    else
        samples_corrected.s = circshift(samples.s,-delay_array(min_idx),1);
    end
end

工学博士，担任《Mechanical System and Signal Processing》审稿专家，担任
《中国电机工程学报》优秀审稿专家，《控制与决策》，《系统工程与电子技术》，《电力系统保护与控制》，《宇航学报》等EI期刊审稿专家。
擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。