#《AI中文版》V3 第 2 章 盲目搜索(Blind Search,也称无信息搜索)
参考链接:
[1] 开源内容:https://github.com/siyuxin/AI-3rd-edition-notes
[2] Kimi Chat官网链接


笔记 P61
本书的目标是介绍用于解决 AI 问题的三个最为流行的方法:搜索、知识表示和学习。
“盲目搜索”或者“无信息搜索”,它们不依赖问题域的任何特定知识。
通常需要大量的空间和时间。
两种经典的搜索方法:贪心算法(greedy algorithm)和回溯法(backtracking)。
两种典型的盲目搜索算法是广度优先搜索(Breath First Search,BFS)和深度优先搜索(Depth First Search,DFS)算法
如果在每个时刻的可选项非常多,那么 BFS 可能会因为需要消耗太多的内存而变得不实用。
DFS 可能会因为偏离起始位置过远而错过相对靠近搜索起始位置的解。
盲目搜索: 寻求发现问题的任意一个解。
知情搜索(Informer Search)算法通常可以发现问题的最优解。
2.2 生成-测试范式 【回溯、贪心】
问题求解的一种直接方式就是先给出可能的解,再检查每个可能的解,看是否有候选解能够构成问题的解。这种方式被称为生成-测试范式(generate-and-test paradigm)。
LeetCode_204. 计数质数
题目链接
题解
下面的常规解法 在该题会超时。
class Solution:
def countPrimes(self, n: int) -> int:
if n == 0 or n == 1:
return 0
res = 0
for i in range(2, n): # 1 不是 素数
if self.check(i):
res += 1
return res
def check(self, num):
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return False #不是 素数
return True
建立一个数组来标记各个数是否为质数;每发现一个质数,就遍历将所有该质数的倍数标记为合数;这种方法叫做“厄拉多塞筛法”。
class Solution:
def countPrimes(self, n: int) -> int:
if n == 0 or n == 1:
return 0
num_list = [True] * n
for i in range(2, int(sqrt(n)) + 1):
if num_list[i]:
for j in range(i * i, n, i): # 倍数 每次增加 i
num_list[j] = False
res = 0
for i in range(2, n):
if num_list[i]:
res += 1
return res
2.2.1 回溯法
回溯法,这是一种将搜索分成多个步骤的搜索过程,每一步都会按照规定的方式做出选择。如果问题的约束条件得到满足,那么搜索将进行到下一步。如果任何选择都得不到可行的部分解,那么搜索将回溯到前一步,撤销前一步的选择,继续下一个可能的选择结果。
2.2.2 贪心算法
Dijkstra 最短路径算法(简称 Dijkstra 算法), 是贪心算法的典型代表。


分支定界(branch and bound)算法是广度优先搜索的一种变体。在这种搜索算法中,节点按照开销不减少的原则进行探索。分支定界算法又称为统一代价搜索(uniform cost search),这种搜索策略可以成功解决旅行商问题的实例。
2.3 盲目搜索算法 (DFS、BFS、DFS-ID)
3 种主要的盲目搜索算法如下:深度优先搜索(DFS)、广度优先搜索(BFS)和迭代加深的深度优先搜索(DFS-ID)。
————————————
讨论题 P84
1.搜索为什么是 AI 系统的重要组成部分?
生活中有很多场景, 如找东西, 姓名、电话记忆等。
1、搜索涉及到在可能的解决方案空间中寻找最佳或最优解。无论是在棋类游戏中寻找最佳走法,还是在复杂的决策问题中选择最佳策略,搜索算法都是实现这些目标的关键。
2、AI系统通常需要处理大量的数据,搜索技术帮助AI从这些数据中提取有用信息,进行分析和推理,从而做出更准确的预测和决策。
3、在自然语言处理中,搜索技术帮助AI理解和生成语言。例如,搜索引擎通过理解用户的查询意图,提供相关的搜索结果,这背后就是搜索算法在工作。
4、随着机器学习和深度学习的发展,搜索技术与这些技术相结合,形成了更强大的AI系统。例如,深度强化学习中的蒙特卡洛树搜索(MCTS)就是一种结合了深度学习和搜索策略的方法。
5、在许多应用场景中,AI系统需要实时响应用户请求。搜索技术通过优化算法和数据处理流程,提高了系统的响应速度和效率。
2.状态空间图是什么?
包含了问题可能出现的所有状态以及这些状态之间所有可能的转换。
3.描述生成-测试范式。
先给出可能的解,再检查每个可能的解,看是否有候选解能够构成问题的解。
4.生成器有什么属性?
生成器模块: 系统地提出了问题的可能解
好的生成器应该是完备、非冗余并且知情的。
5.回溯法如何对完全枚举法进行改进?
回溯法一旦发现一个部分解违反了问题的约束条件,就放弃这个部分解。通过这种方式,回溯法缩短了搜索时间。
6.用一两句话描述贪心算法。
贪心算法是一种搜索范式,它在求解诸如在城市之间寻找最短路径的问题中非常有用。然而,贪心算法并不适合所有问题。例如,它没有成功地解决旅行商问题。
7.陈述旅行商问题。
贪心在该问题上存在不足, 统一代价搜索算法 是更好的 解决方案。

8.简述 3 种盲目搜索算法。
3 种盲目搜索算法分别是广度优先搜索(BFS)、深度优先搜索(DFS)和迭代加深的深度优先搜索(DFS-ID)。
其中,BFS在搜索求解问题时,按层次遍历树。BFS 是完备和最优的(在各种约束下)。然而,BFS 过量的空间需求使其应用受到了阻碍。
虽然DFS有可能变得非常长或迷失在无限的路径中,但是 DFS 的空间需求相对合理。因此,DFS 既不是完备的也不是最优的。
DFS-ID可以作为 BFS 和 DFS 的折中;在搜索树上,尤其是在深度为 0、1、2 等受限深度的搜索树上,DFS-ID 执行的是一个完备的 DFS 搜索过程。换句话说,DFS-ID 同时具有 DFS 和 BFS 的优点,即 DFS 的中等存储空间需求以及 BFS 的完备性和最优性。
9.在何种意义上,盲目搜索算法是盲目的?
不知道状态空间的任何信息。
10.按照完备性、最优性和时空复杂性,比较本章描述的 3 种盲目搜索算法。
完备且最优: BFS、DFS_ID。 非完备非最优: DFS
时空复杂性: BFS(需要最多) > DFS_ID > DFS
11.在什么情况下,DFS 比 BFS 好?
在每个时刻的可选项非常多
12.在什么情况下,BFS 比 DFS 好?
搜索深度很大,而所求的解离根很近。
13.在什么意义上,可以说 DFS-ID 是 BFS 和 DFS 的折中?
在深度为 0、1、2 等受限深度的搜索树上.
结合 DFS 的中等存储空间需求,去除寻找长路径的倾向,可以得到迭代加深的 DFS,即 DFS-ID(DFS With Iterative Deepening)。
练习题 P84
1.在只允许称重 3 次的情况下,求解 12 枚硬币的假币问题。回忆一下,天平可以返回以下 3 种结果之一:相等、左侧轻或左侧重。
4 :4 : 4 称 1次
2.在只称重两次的情况下,求解微型假币问题或证明这是不可能的。
- 需要至少三次称重来确定假币。
3.非确定性搜索(nondeterministic search)是本章未讨论的一种盲目搜索方法。在这种搜索中,刚刚扩展的子节点以随机顺序放在开放表中。请判断非确定性搜索是否完备以及是否最优。
完备性是指搜索方法能够找到问题的解(如果存在的话)。非确定性搜索是完备的,因为它最终会访问所有可能的状态空间。由于它是盲目搜索的一种形式(不使用启发式信息),它不会跳过任何可能的节点。在最坏的情况下,非确定性搜索会遍历整个搜索树,直到找到目标节点或确定不存在解。
最优性是指搜索方法能够找到问题的最优解(如果存在的话)。非确定性搜索并不保证最优解。由于它是随机选择下一个要扩展的节点,它可能会错过更优的路径,而选择一个次优的路径。在某些情况下,它可能会偶然找到最优解,但这完全依赖于随机选择的结果,而不是任何策略性的决策。
- 在实际应用中,非确定性搜索通常用于那些最优解不是关键因素的问题,或者作为其他搜索算法(如A*搜索)的随机化变体来避免局部最优解。
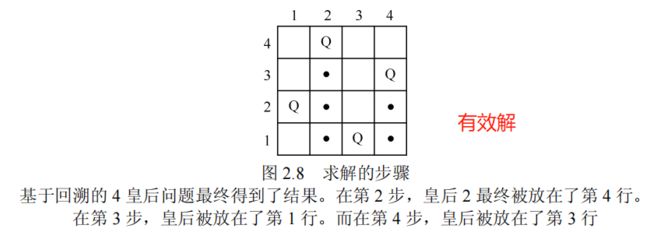
4.n 皇后问题的另一个生成器如下:第一个皇后放在第一行,第二个皇后不放在受第一个皇后攻击的任何方格中。在状态 i,将第 i 列的皇后放在未受前面(i−1)个皇后攻击的方格中,
如图 2.34 所示。
(a)使用这个生成器求解 4 皇后问题。
(b)证明这个生成器比文中使用的两个生成器拥有更多的信息。
- 这个生成器在每一步都利用了之前步骤的信息, 减少了无效的尝试,提高了搜索效率。
(c)画出搜索第一个解时在搜索树中展开的部分。
5.思考下列 4 皇后问题的生成器:从 i=1 到 i=4,随机地分配皇后 i 到某一行。这个生成器完备吗?非冗余吗?解释你的答案。
完备性:这个随机生成器理论上可以产生所有可能的配置,包括那些满足四皇后问题条件的配置。因此,从这个角度来看,它是完备的。
非冗余性: 这个生成器并不是非冗余的。因为它会随机地为每个皇后选择位置,所以它可能会产生相同的配置多次。例如,如果随机选择的结果是每个皇后都放在第一行,那么这个配置会重复出现,尽管它并不是一个有效的解决方案(因为皇后们会相互攻击)。
6.如果一个数等于其因数(不包括这个数本身)的和,则称这个数是完美数。例如,6 是完美数,因为 6 = 1 + 2 + 3,其中整数 1、2 和 3 都是 6 的因数。给出你所能想到的拥有最多信息的生成器,使用这个生成器,可以找到 1 和 100 之间(包括 1 和 100 在内)的所有完美数。
√ LeetCode_完美数
LeetCode链接
class Solution:
def checkPerfectNumber(self, num: int) -> bool:
if num == 1:
return False
total = 1
for i in range(2, int(sqrt(num)) + 1):
if num % i == 0:
total += i + num / i
return total == num
class Solution {
public:
bool checkPerfectNumber(int num) {
if (num == 1){
return false;
}
int total = 1;
for (int i = 2; i <= num / i; ++i){
if (num % i == 0){
total += i;
if (num / i != i){
total += num / i;
}
}
}
return total == num;
}
};
7.使用 Dijkstra 算法找到从源顶点 V0到所有其他顶点的最短路径,如图 2.35 所示。
√ LeetCode_ 847. 访问所有节点的最短路径 ⟮ O ( n 2 ⋅ 2 n ) 、 O ( n ⋅ 2 n ) ⟯ \lgroup O(n^2 · 2^n)、O(n · 2^n)\rgroup ⟮O(n2⋅2n)、O(n⋅2n)⟯
题目链接
class Solution:
def shortestPathLength(self, graph: List[List[int]]) -> int:
# 基于 状态压缩 的 多源 BFS
n = len(graph)
q = deque((i, 1 << i, 0) for i in range(n)) # 起始结点, 状态, 距离
visited = {(i, 1 << i) for i in range(n)} # 结点, 状态
while q:
node, mask, dist = q.popleft()
if mask == (1 << n) - 1:
return dist # 多源 BFS, 最先返回 即为 最短路径
for x in graph[node]:
nextmask = mask | (1 << x) # 更新 mask
if (x, nextmask) not in visited:
q.append((x, nextmask, dist + 1))
visited.add((x, nextmask))
return 0
class Solution {
public:
int shortestPathLength(vector<vector<int>>& graph) {
int n = graph.size();
queue<tuple<int, int, int>> q;
vector<vector<int>> visited(n, vector<int>(1 << n));
for (int i = 0; i < n; ++i){
q.emplace(i, 1 << i, 0);
visited[i][1 << i] = true;
}
while (!q.empty()){
auto [u, mask, dist] = q.front();
q.pop();
if (mask == (1 << n) - 1){
return dist;
}
// 搜索 下一个
for (int v : graph[u]){
int mask_v = mask | (1 << v);
if (!visited[v][mask_v]){
q.emplace(v, mask_v, dist + 1);
visited[v][mask_v] = true;
}
}
}
return 0;
}
};
图 2.34 4 皇后问题的生成器 图 2.35 使用 Dijkstra 算法的标记图
8.创建拼图(如 15 拼图)的表示以适合检查重复状态。
9.使用广度优先搜索求解传教士与野人问题。
10.在河的西岸,一个农夫带着一匹狼、一只山羊和一篮子卷心菜(参见图 2.0)。河上有一艘船,可以装下农夫以及狼、山羊、卷心菜三者中的一个。如果留下狼与羊单独在一起,那么狼会吃掉羊。如果留下羊与卷心菜单独在一起,那么羊会吃掉卷心菜。现在的目标是将它们都安全地转移到河的对岸。请分别使用以下搜索算法解决上述问题:
(a)深度优先搜索;
(b)广度优先搜索
11.首先使用 BFS,然后使用 DFS,从图 2.36(a)和图 2.36(b)的起始节点 S 开始,最终到达目标节点 G。其中每一步都按照字母表顺序浏览节点。
12.标记图 2.37 所示的迷宫。
13.对于图 2.37 所示的迷宫,先使用 BFS,再使用 DFS,从起点处开始走到目标处。
14.我们已经确定,12 枚硬币的假币问题需要对 3 组硬币进行称重才能确定假币。那么在15 枚硬币中,需要称重多少次才可以确定假币?20 枚硬币时又会怎么样?请开发出一种算法来证明自己的结论。
提示:可以先考虑 2~5 枚硬币所需的基本称量次数,从而开发出事实知识库,自底向上得到这个问题的解。

15.我们讨论了传教士与野人问题。假定“移动”或“转移”是强行(受迫)的,找出这个问题的一个解。确定问题解决状态的“子目标状态”,我们必须获得这个状态,才能解决这个问题。
编程题 P87
—LeetCode 相关
LeetCode_迷宫
链接
LeetCode_1036. 逃离大迷宫
题目链接
方法: BFS ⟮ O ( n 2 ) ⟯ \lgroup O(n^2) \rgroup ⟮O(n2)⟯
BOUND = int(1e6)
class Solution:
def isEscapePossible(self, blocked: List[List[int]], source: List[int], target: List[int]) -> bool:
blocked, MAX = {tuple(p) for p in blocked}, len(blocked) * (len(blocked) - 1) // 2
def bfs(start, end):
q = [start]
idx = 0
visited = {tuple(start)}
while idx < len(q):
for dx, dy in (0, 1), (1, 0),(-1, 0),(0, -1): # 一圈圈 往外 找
x, y = q[idx][0], q[idx][1]
nx, ny = x + dx, y + dy
if 0 <= nx < BOUND and 0 <= ny < BOUND and (nx, ny) not in blocked and (nx, ny) not in visited:
if [nx, ny] == end:
return True
visited.add((nx, ny))
q.append((nx, ny))
if len(q) > MAX:
return True
idx += 1
return False
return bfs(source, target) and bfs(target, source)
1210. 穿过迷宫的最少移动次数
题目链接
方法:BFS ⟮ O ( n 2 ) ⟯ \lgroup O(n^2) \rgroup ⟮O(n2)⟯
class Solution:
def minimumMoves(self, grid: List[List[int]]) -> int:
# 旋转 算一次 因此 需要记录状态
step = 1
n = len(grid)
visited = {(0, 0, 0)} # 记录
q = [(0, 0, 0)] # 存储 蛇尾 位置
while q:
cur_len = len(q)
for _ in range(cur_len):
X, Y, S = q.pop(0)
for t in (X + 1, Y, S), (X, Y + 1, S), (X, Y, S ^ 1): # 向右, 向下, 旋转
x, y, s = t
x2, y2 = x + s, y + (s ^ 1) # 蛇头位置
if x2 < n and y2 < n and t not in visited and \
grid[x][y] == 0 and grid[x2][y2] == 0 and (s == S or grid[x + 1][y + 1] == 0): # 旋转 时 斜下方的格也要 为 0
if x == n - 1 and y == n - 2: # 蛇尾 位置
return step
visited.add(t)
q.append(t)
step += 1
return -1
LeetCode_ LCR 129. 字母迷宫
题目链接
题解链接
方法: 回溯 ⟮ O ( M N ⋅ 3 L ) 、 O ( M N ) ⟯ \lgroup O(MN · 3^L)、O(MN)\rgroup ⟮O(MN⋅3L)、O(MN)⟯
class Solution:
def wordPuzzle(self, grid: List[List[str]], target: str) -> bool:
def dfs(row, col, i): # 遍历的 横纵 下标。 target 的 遍历下标
if not 0 <= row < len(grid) or not 0 <= col < len(grid[0]) or grid[row][col] != target[i]:
return False
if i == len(target) - 1:
return True # 找到 路径了
# 找到 与 字符 target[i] 匹配的 位置了
grid[row][col] = '' # 修改, 表明 访问过
res = dfs(row + 1, col, i + 1) or dfs(row - 1, col, i + 1) or dfs(row, col + 1, i + 1) or dfs(row, col - 1, i + 1)
grid[row][col] = target[i] ## 恢复。 有点 回溯的意思
return res
for row in range(len(grid)):
for col in range(len(grid[0])):
if dfs(row, col, 0):
return True
return False
class Solution {
public:
bool wordPuzzle(vector<vector<char>>& grid, string target) {
for (int i = 0; i < grid.size(); ++i){
for (int j = 0; j < grid[0].size(); ++j){
if (dfs(grid, target, i, j, 0)){
return true;
}
}
}
return false;
}
bool dfs(vector<vector<char>>& grid, string target, int i, int j, int k){
int rows = grid.size();
int cols = grid[0].size();
if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] != target[k]){
return false;
}
if (k == target.size() - 1){
return true;
}
grid[i][j] = '#';
bool res = dfs(grid, target, i + 1, j, k + 1) || dfs(grid, target, i - 1, j, k + 1) || dfs(grid, target, i, j + 1, k + 1) || dfs(grid, target, i, j - 1, k + 1);
grid[i][j] = target[k];
return res;
}
};
√ LeetCode_N皇后
链接
51. N 皇后
题目链接
判断该位置所在的列和两条斜线上是否已经有皇后。
同一条斜线上的每个位置满足行下标与列下标之差相等
方法一: 基于集合的回溯 ⟮ O ( N ! ) 、 O ( N ) ⟯ \lgroup O(N!)、O(N)\rgroup ⟮O(N!)、O(N)⟯
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
def backtrack(row):
if row == n:
res.append(['.' * c + 'Q' + '.' * (n - 1 - c) for c in queens]) # 添加到 结果中。 c 就是 queen 的 列下标, 刚好 提供长度信息
else:
for i in range(n): # 遍历 列的位置
if i in columns or row - i in diagonal1 or row + i in diagonal2:
continue # 不能放
queens[row] = i # 第 row 行 放了 Q
columns.add(i)
diagonal1.add(row - i) ## 记录 差
diagonal2.add(row + i) ## 记录和
backtrack(row + 1)
columns.remove(i)
diagonal1.remove(row - i)
diagonal2.remove(row + i)
res = []
queens = [-1] * n # 记录 该列 是否 有 皇后
columns = set()
diagonal1 = set() # 记录 主斜线 行列 下标差值
diagonal2 = set() # 副斜线 行列下标之和
row = ["."] * n
backtrack(0)
return res
方法二:基于位运算的回溯 复杂度一样, 但不太好理解。先放着。
52. N 皇后 II
题目链接
class Solution:
def totalNQueens(self, n: int) -> int:
def backtrack(row):
if row == n:
return 1
else:
cnt = 0
for i in range(n):
if i in columns or row - i in diagonal1 or row + i in diagonal2:
continue
queens[row] = i
columns.add(i)
diagonal1.add(row - i)
diagonal2.add(row + i)
cnt += backtrack(row + 1) ## 重要
columns.remove(i)
diagonal1.remove(row - i)
diagonal2.remove(row + i)
return cnt
queens = [-1] * n
columns = set()
diagonal1 = set()
diagonal2 = set()
return backtrack(0)
class Solution:
def totalNQueens(self, n: int) -> int:
def backtrack(row):
nonlocal res
if row == n:
res += 1
else:
for i in range(n):
if i in columns or row - i in diagonal1 or row + i in diagonal2:
continue
queens[row] = i
columns.add(i)
diagonal1.add(row - i)
diagonal2.add(row + i)
backtrack(row + 1) ## 重要
columns.remove(i)
diagonal1.remove(row - i)
diagonal2.remove(row + i)
res = 0
queens = [-1] * n
columns = set()
diagonal1 = set()
diagonal2 = set()
backtrack(0)
return res
返回之前的地方
1222. 可以攻击国王的皇后
方法: 从皇后出发, 计算距离,选最近的 ⟮ O ( n ) 、 O ( 1 ) ⟯ \lgroup O(n)、O(1)\rgroup ⟮O(n)、O(1)⟯
class Solution:
def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:
def direction(x):
return 1 if x > 0 else (0 if x == 0 else -1) # 构造 8个方向
candidates = defaultdict(lambda: (None, inf))
kx, ky = king
for qx, qy in queens:
x, y = qx - kx, qy - ky
if x == 0 or y == 0 or abs(x) == abs(y):
dx, dy = direction(x), direction(y)
if candidates[(dx, dy)][1] > abs(x) + abs(y):
candidates[(dx, dy)] = ([qx, qy], abs(x) + abs(y))
res = [value[0] for value in candidates.values()]
return res
3001. 捕获黑皇后需要的最少移动次数
class Solution:
def minMovesToCaptureTheQueen(self, a: int, b: int, c: int, d: int, e: int, f: int) -> int:
# 白色车 (a, b)
# 白色象 (c, d)
# 黑皇后 (e, f)
# 车同行 无遮挡 直接攻击 b d f
# 车同列 无遮挡 直接攻击 a c e
# 象 同 斜线 无遮挡 直接攻击 # 主斜线: 行列下标差 一致 遮挡则:c a e
if a == e and not (c == e and (d - b) * (d - f) < 0) or \
b == f and not (d == f and (c - a) * (c - e) < 0) or \
c + d == e + f and not (a + b == e + f and (a - c) * (a - e) < 0) or \
c - d == e - f and not (a - b == e - f and (a - c) * (a - e) < 0): # 副斜线 行列下标和 一致。 若遮挡 则 c a e
return 1
return 2
▢ LeetCode 算法笔记
内容挺多, 有空再补。。
- 04.03 回溯算法(第 07 ~ 09 天)
链接 - 04.04 贪心算法(第 10 ~ 12 天)
链接 - 02.03 深度优先搜索DFS(第 08 ~ 10 天)
链接:深度优先搜索(第 08 ~ 10 天) - 02.05 广度优先搜索(第 13 ~ 14 天)
链接