LeetCode-429. N 叉树的层序遍历【层序遍历代码模板】

题目描述：push可以都改为emplace效率更高！！！

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

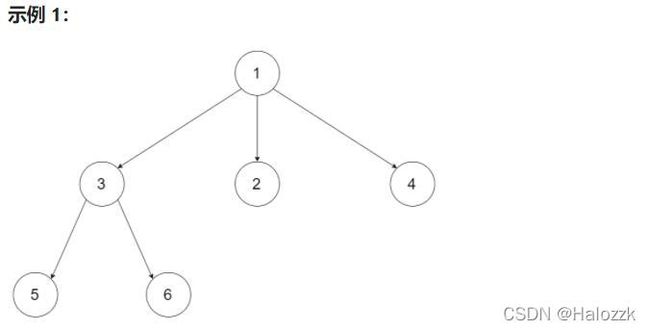
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

解题思路一：队列实现，每次记录一层节点的大小，方便循环出队。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector children;//孩子节点是一个指针，一个指针指向一堆子节点

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        vector<vector<int>> ans;//最终结果
        queue<Node*> que;//一个记录指针的队列
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            vector<int> vc;//vc局部变量，每次记录一层的节点。
            int size=que.size();//size每次记录一层的节点数
            for(int i=0;i<size;++i){//处理当前层节点
                Node* node=que.front();
                vc.emplace_back(node->val);//存当前层的节点
                que.pop();
                for(int j=0;j<node->children.size();++j){// 将节点孩子加入队列
                    if(node->children[j]) que.push(node->children[j]);
                }
            }
            ans.emplace_back(vc);
        }
        return ans;
    }
};

解题思路二：层序遍历代码模板。

1.有根，根入队
2.while，队列不空。
3.记录当前层的size进行for循环处理当前层节点（即pop队列size次）
4.当前层子节点入队
5.将当前层节点加入最终结果，回到2。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

复杂度分析

时间复杂度：O(n)，其中 n 是树中包含的节点个数。在广度优先搜索的过程中，我们需要遍历每一个节点恰好一次。

空间复杂度：O(n)，即为队列需要使用的空间。在最坏的情况下，树只有两层，且最后一层有 n−1 个节点，此时就需要 O(n) 的空间。