动态规划算法

一、动态规划算法思想

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

　　动态规划算法与分治法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）

这么一大坨概念，反正我刚学的时候是没看懂，后来自己写了两个例子就明白啥是动态规划了

二、示例

1.经典的上楼梯问题

(1).解题思路

问题: 楼梯有n阶一次只能上一阶或者两阶，求有多少种上法。

如果我们没有学过动态规划估计是这样想: a + 2b = n a 和 b 大于等于0，然后去搞排列组合，想想就麻烦，下面我们用动态规划的思想：

如果只有一阶楼梯，那毫无疑问 只有一种上法 f(1) = 1;

如果只有两阶楼梯，有两种上法 f(2) = 2；

如果有三阶楼梯，f(3) = f(3 - 1) + f(3 - 2) 重点是这里，在我们上三阶楼梯的时候可以迈一步或者迈两步 即 f(3 - 1) 从第二阶上来和 f(3 - 2)从第1阶上来，而f(2)和f(1)我们已经知道是几种，所以就能算出来 f(3) = 3 

推广成n就是 f(n) = f(n - 1) + f(n - 2) 这个f(n)就是上n阶楼梯有多少种上法，这就是动态规划的中心思想即把一个大问题f(n)变成了两个小问题f(n - 1)和f(n - 2)，然后继续把两个小问题变成更小的问题，直到问题小到易得答案f(1) = 1,f(2) = 2。

(2).代码实现

public class GoUpStairs {
    //有20级台阶，一个人每次上一级或者两级，问有多少种走完20级台阶的方法。
    static long[] upMethod;

    public static void main(String[] args) {
        int n = 20;
        upMethod = new long[n + 1];
        for (int i = 1; i <= n; i++) { // 这个循环就能求出所有阶楼梯的上法
            upMethod[i] = upStairs(i);
        }
        System.out.println(upStairs(n)); // 只算n阶楼梯的上法
    }

    //n 是f(n)中的n
    public static long upStairs(int n) {
        if (upMethod[n] != 0) { // 避免重复计算
            return upMethod[n];
        }

        if (n == 1 || n == 2) { //已知第一阶和第二阶的上法
            return n;
        }

        return upStairs(n - 1) + upStairs(n - 2); //n阶楼梯的上法等于 n - 1和 n - 2阶楼梯上法的和
    }
}

2.经典矩阵问题

(1).问题描述

给定一个矩阵m，从左上角开始每次只能向右走或者向下走，最后达到右下角的位置，路径中所有数字累加起来就是路径和，问(0,0)到每一个点分别有几种走法（几条路径），到每一个点的最小路径和是多少。

(2).从(0,0)到每一个点有几种走法。

我们继续用动态规划的思想分析:

到(m,n)这个点，只能通过(m - 1, n)或者 (m,n - 1)这两个点即:

f(m,n) = f(m - 1,n) + f(m,n - 1)  ，f(m,n)函数的意思就是(0,0)到(m,n)有几条路径

那分到什么程度，才是易得答案呢，分到(m,n)坐标的其中一个是0的时候，因为是从左上角开始每次只能向右走或者向下走，当有一个是0的时候说明这个坐标在矩形的左边界或者上边界，这是从(0,0)到这个点只有一条路径。

代码实现:

public class MatrixShortestPath {
    public static int[][] matrix = {{1, 3, 5, 9}, {8, 1, 3, 4}, {5, 0, 6, 1}, {8, 8, 4, 0}};

    public static void main(String[] args) {
        hasSeveralPaths();
    }

    public static void hasSeveralPaths() {
        int[][] result = new int[matrix.length][matrix[0].length];
        for (int m = 0; m < matrix.length; m++) {
            for (int n = 0; n < matrix[m].length; n++) {
                result[m][n] = severalPaths(m, n, result);
                System.out.print(result[m][n] + " ");
            }
            System.out.println();
        }
    }

    //从 (0,0) 开始 到 (m,n) 有多少种走法
    public static int severalPaths(int m, int n, int[][] result) {
        if (m == 0 || n == 0) { // 位于两边的只有一种走法
            return 1;
        }

        if (result[m][n] != 0) {
            return result[m][n];
        }

        return severalPaths(m - 1, n, result) + severalPaths(m, n - 1, result);
    }


}

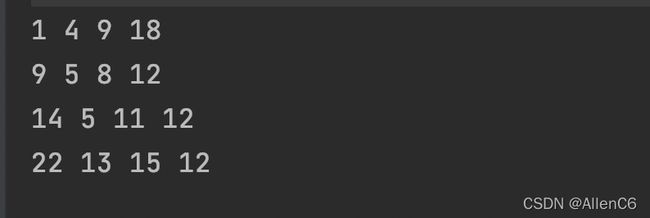
运行结果:

(3).求从(0,0)到每一个点的最小路径和

 思想，和上面类似，只不过f(m,n)的含义是(0,0)到(m,n)的最小路径和，因为是从左上角开始每次只能向右走或者向下走，只要我们知道一个点的左边的点和上边的点的最小路径和，比较这两个点的大小，用小的路径和加上当前点的值就是(0,0)到当前点的最小路径和即:

f(m,n) = Min( f(m - 1, n)  , f(m,n - 1) )  +  坐标(m,n)显示的值

易得最小问题也是，在矩阵的上边界和左边界，因为(0,0)到上边界和左边界的点路径只有一条，所以最小路径和是确定的。我们求出上边界和左边界的所有点的最小路径和之后，就能通过公式继续一步一步的求下面的点的最小路径和。

代码实现:

public class MatrixShortestPath {
    public static int[][] matrix = {{1, 3, 5, 9}, {8, 1, 3, 4}, {5, 0, 6, 1}, {8, 8, 4, 0}};

    public static void main(String[] args) {
        shortestPathSum();
    }



    //求从(0,0)到(m,n)的最小路径和,先计算(0,0)到两边的每个点的最小路径和,然后再
    public static void shortestPathSum() {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] result = new int[m][n];
        result[0][0] = matrix[0][0];

        for (int i = 1; i < m; i++) { // 位于x轴上的只有一条路，每个点的最小路径和就是从 (0,0) 横着加到当前坐标(m,0)
            result[i][0] = matrix[i][0] + result[i - 1][0];
        }

        for (int i = 1; i < n; i++) {// 位于y轴上的只有一条路，每个点的最小路径和就是从 (0,0) 竖着加到当前坐标(0,n)
            result[0][i] = matrix[0][i] + result[0][i - 1];
        }

        //上面计算出了从(0,0)到矩阵两个边每一点的最小路径和，接下来我们依托这两个边，给剩下的点依次求最小路径和
        //因为有一个规则是只能从左上角向右或者向下移动，这就代表着只要知道一个坐标的上边和左边的最小路径和，比较它们的大小，选取小的，加上当前坐标
        //就是(0,0)到当前坐标的最小路径和  注意理解:需要知道当前坐标左边和上边的坐标的最小路径和
        for (int x = 1; x < matrix.length; x++) {
            for (int y = 1; y < matrix[x].length; y++) {
                if (result[x][y] != 0) {
                    continue;
                }
                result[x][y] = Math.min(result[x - 1][y] + matrix[x][y], result[x][y - 1] + matrix[x][y]);
            }
        }

        //最后这个是打印用的
        for (int x = 0; x < matrix.length; x++) {
            for (int y = 0; y < matrix[x].length; y++) {
                System.out.print(result[x][y] + " ");
            }
            System.out.println();
        }
    }


}

执行结果：

3. 求两个字符串的最长公共子序列

注意区分最长公共子序列和最长公共子串，最长公共子序列可以不连续，最长公共子串是连续的。

(1).暴力解法

思想: 

假设两个字符串分别为A=a1a2..am,B=b1b2..bn,则m为A的长度，n为B的长度。那么他们的最长公共子序列分为两种情况:

1).am=bn,这时他们的公共子序列一定为的长度F(m,n)=F(m-1,n-1)+am；

2).am≠bn,这时他们的公共子序列一定为的长度F(m,n)=Max(F(m-1,n),F(m,n-1))；

代码实现:

    public static String s1 = "357486782";
    public static String s2 = "13456778";
    public static String[][] strArr = new String[s1.length()][s2.length()];

    public static void main(String[] args) {
        firstGet(s1,s2);
    }

    public static void firstGet(String s1, String s2) {
        int m = s1.length() - 1;
        int n = s2.length() - 1;
        System.out.println(commonSubsequence(m, n));
        System.out.println(count);
    }

    public static int count = 0;
    //初版
    public static String commonSubsequence(int m, int n) {
        count++;
        if (m < 0 || n < 0) {
            return "";
        }
        if (s1.charAt(m) == s2.charAt(n)) {
            return commonSubsequence(m - 1, n - 1) + s1.charAt(m);
        } else {
            String str1 = commonSubsequence(m - 1, n);
            String str2 = commonSubsequence(m, n - 1);
            return str1.length() > str2.length() ? str1 : str2;
        }
    }

运行结果:

count值是5723，执行了5723次

(2).插一个求两个字符串的最长公共子序列的长度

s1 = a0...am  , s2 = b0.....bn

设f(m,n)为a1...am 和 b1...bn的最长公共子序列的长度

f(m,n) =

1). f(m - 1, n - 1) + 1 ， am = bn

如果am = bn，那a0...am和b0...到bn的最长公共子序列的长度为，a0....am-1和b0...bn-1的最长公共子序列长度 + 1

2).Max( f(m - 1,n) , f(m,n-1)) ，am != bn 

如果am != bn，那a0...am和b0...bn的最长公共子序列就是，a0...am和b0...bn-1或a0...am-1和b0...bn，看哪个大就是哪个

3). f(0,n) = 0; //注意这个0指不是字符串的第0位(第一个字符)，而是空串，即空串和任何字符串比较都没有共同的部分，写代码的时候要注意

4). f(m,0) = 0; //注意这个0指不是字符串的第0位(第一个字符)，而是空串，即空串和任何字符串比较都没有共同的部分，写代码的时候要注意

看到上面的公式感觉和矩阵那个最小路径和有点像，都是坐标带0的都是0（动态规划的易得答案），矩阵的f(m,n)的意思是从(0,0)到(m,n)的最小路径和，因为只能向右或向下移动，所以只需要比较f(m-1,n)和f(m,n - 1)的大小，取较小的加上当前的坐标显示的值就是(0,0)到(m,n)最小路径和，所以公式是f(m,n) = Min( f(m - 1, n)  , f(m,n - 1) )  +  坐标(m,n)显示的值，而求最长公共子序列的长度和求矩阵最小路径和相比只是换了一下行进的条件。

代码实现:

    //优化版求最长公共子序列的长度
    public static void commonSubsequenceLength() {
        int m = s1.length();
        int n = s2.length();
        int[][] commonLengthArr = new int[m + 1][n + 1];

        for (int i = 0; i < m + 1; i++) { // 0现在不代表第一个字符，代表第0个字符即空串,空串和任何字符比较都不可能相等所以都是0
            commonLengthArr[i][0] = 0;
        }

        for (int i = 0; i < n + 1; i++) { // 0现在不代表第一个字符，代表第0个字符即空串,空串和任何字符比较都不可能相等所以都是0
            commonLengthArr[0][i] = 0;
        }

        for (int i = 1; i < m + 1; i++) { // 字符串比较从1开始，0不在代表第一个字符，就是代表空串
            for (int j = 1; j < n + 1; j++) {
                char a = s1.charAt(i - 1); //实际取字符串的时候还是要取第0个
                char b = s2.charAt(j - 1);
                if (a == b) {
                    commonLengthArr[i][j] = commonLengthArr[i - 1][j - 1] + 1;
                } else {
                    commonLengthArr[i][j] = Math.max(commonLengthArr[i - 1][j], commonLengthArr[i][j - 1]);
                }
            }
        }

        for (int i = 0; i < m + 1; i++) { //这个就是为了遍历一下
            for (int j = 0; j < n + 1; j++) {
                System.out.print(commonLengthArr[i][j]);
            }
            System.out.println();
        }
    }

(3).优化解法求两个字符串的最长公共子序列

1).

我们已经知道最大长度是多少了，如何知道这个公共子序列具体是啥，我们从f(m,n)反推，如果

am = bn, 那am这个字符应在最长公共子序列中，我们知道是从f(m - 1, n - 1) + am过来的，

如果am ！= bn，则 f(m,n)是从 f(m,n - 1)和f(m - 1,n)中较大的那个过来的，以这个逻辑可以从am，bn推算到a0，b0，整个路径就知道了，我们把这个路径中am = bn的放到公共子序列中，那最大公共子序列就找到了

代码:

    //优化版获取最长公共子序列
    public static void commonSubsequence() {
        count = 0;
        int m = s1.length();
        int n = s2.length();
        int[][] commonLengthArr = new int[m + 1][n + 1];
        String[][] commonStrArr = new String[m][n];

        for (int i = 0; i < m + 1; i++) { // 0现在不代表第一个字符，代表第0个字符即空串,空串和任何字符比较都不可能相等所以都是0
            commonLengthArr[i][0] = 0;
            count++;
        }

        for (int i = 0; i < n + 1; i++) { // 0现在不代表第一个字符，代表第0个字符即空串,空串和任何字符比较都不可能相等所以都是0
            commonLengthArr[0][i] = 0;
            count++;
        }

        for (int i = 1; i < m + 1; i++) { // 字符串比较从1开始，0不在代表第一个字符，就是代表空串
            for (int j = 1; j < n + 1; j++) {
                char a = s1.charAt(i - 1); //实际取字符串的时候还是要取第0个
                char b = s2.charAt(j - 1);
                if (a == b) {
                    commonLengthArr[i][j] = commonLengthArr[i - 1][j - 1] + 1;
                    commonStrArr[i - 1][j - 1] = "入"; //相同的需要加入我们的LCS的串中
                } else {
                    commonLengthArr[i][j] = Math.max(commonLengthArr[i - 1][j], commonLengthArr[i][j - 1]);
                    if (commonLengthArr[i - 1][j] >= commonLengthArr[i][j - 1]) {
                        commonStrArr[i - 1][j - 1] = "左";
                    } else {
                        commonStrArr[i - 1][j - 1] = "上";
                    }
                }
                count++;
            }
        }

        for (int i = 0; i < m; i++) { //这个就是为了遍历一下
            for (int j = 0; j < n; j++) {
                System.out.print(commonStrArr[i][j]);
                count++;
            }
            System.out.println();
        }

        StringBuilder stringBuilder = new StringBuilder();
        int i = m - 1, j = n - 1;
        while (i >= 0 && j >= 0) {
            count++;
            if (commonStrArr[i][j].equals("入")) {
                stringBuilder.append(s1.charAt(i));
                i--;
                j--;
            } else if (commonStrArr[i][j].equals("左")) {
                i--;
            } else if (commonStrArr[i][j].equals("上")) {
                j--;
            }
        }

        System.out.println(stringBuilder.reverse().toString());
        System.out.println("count:" + count);
    }

2). 模仿一下求最长公共子序列长度的代码

f(m,n)为从a0,b0到 am,bn的最大公共子序列

换成公式 f(m,n) =  

1). f(m - 1,n - 1) + am , am =  bn

2). Max( f(m - 1,n) , f(m,n-1)) ，am != bn 

    //优化版获取最长公共子序列1
    public static void commonSubsequence1() {
        count = 0;
        int m = s1.length();
        int n = s2.length();
        String[][] commonLengthArr = new String[m + 1][n + 1];

        for (int i = 0; i < m + 1; i++) { // 0现在不代表第一个字符，代表第0个字符即空串,空串和任何字符比较都不可能相等所以都是0
            commonLengthArr[i][0] = "";
            count++;
        }

        for (int i = 0; i < n + 1; i++) { // 0现在不代表第一个字符，代表第0个字符即空串,空串和任何字符比较都不可能相等所以都是0
            commonLengthArr[0][i] = "";
            count++;
        }

        for (int i = 1; i < m + 1; i++) { // 字符串比较从1开始，0不在代表第一个字符，就是代表空串
            for (int j = 1; j < n + 1; j++) {
                char a = s1.charAt(i - 1); //实际取字符串的时候还是要取第0个
                char b = s2.charAt(j - 1);
                if (a == b) {
                    commonLengthArr[i][j] = commonLengthArr[i - 1][j - 1] + a;
                } else {
                    if (commonLengthArr[i - 1][j].length() >= commonLengthArr[i][j - 1].length()) {
                        commonLengthArr[i][j] = commonLengthArr[i - 1][j];
                    } else {
                        commonLengthArr[i][j] = commonLengthArr[i][j - 1];
                    }
                }
                count++;
            }
        }

        for (int i = 0; i < m + 1; i++) { //这个就是为了遍历一下
            for (int j = 0; j < n + 1; j++) {
                System.out.print(commonLengthArr[i][j] + "  ");
                count++;
            }
            System.out.println();
        }

    }