【LeetCode】106. 从中序与后序遍历序列构造二叉树（中等）——代码随想录算法训练营Day18

题目链接：106. 从中序与后序遍历序列构造二叉树

题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

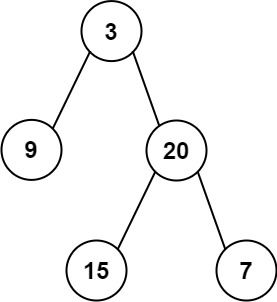
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

文章讲解：代码随想录

视频讲解：坑很多！来看看你掉过几次坑 | LeetCode：106.从中序与后序遍历序列构造二叉树_哔哩哔哩_bilibili

题解1：递归法

思路：递归的构造二叉树，分为以下几步：

• 如果后序数组为空，直接返回空节点；
• 不为空，则取后序数组最后一个元素为根节点；
• 找到后序数组最后一个元素在中序数组中的位置，记为 index，作为切割点；
• 切割中序数组，[0, index) 为左中序数组，[index + 1, inorder.length) 为右中序数组；
• 切割后序数组，[0, index) 为左后序数组，[index, postorder.length - 1) 为右后序数组；
• 以左中序数组和左后序数组递归的构建左子树，以右中序数组和右后序数组递归的构建右子树。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function(inorder, postorder) {
    if (postorder.length === 0) {
        return null;
    }
    const rootVal = postorder[postorder.length - 1]; // 后序数组最后一个元素为根节点
    const root = new TreeNode(rootVal); // 创建根节点
    if (postorder.length === 1) {
        return root; // 当后序数组长度为1时，说明是叶子节点，直接返回这个节点
    }
    const index = inorder.indexOf(rootVal);
    root.left = buildTree(inorder.slice(0, index), postorder.slice(0, index)); // 根据左中序数组和左后序数组构建左子树
    root.right = buildTree(inorder.slice(index + 1), postorder.slice(index, postorder.length - 1)); // 根据右中序数组和右后序数组构建右子树
    return root;
};

分析：时间复杂度为 O(nlogn)，空间复杂度为 O(nlogn)。

同类题 105. 从前序与中序遍历序列构造二叉树

题目链接：105. 从前序与中序遍历序列构造二叉树

思路：与从中序与后序遍历序列构造二叉树方法类似，切割序列的区间不同。

递归法

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    if (preorder.length === 0) {
        return null;
    }
    const rootVal = preorder[0]; // 前序数组第1个元素为根节点
    const root = new TreeNode(rootVal); // 创建根节点
    if (preorder.length === 1) {
        return root; // 当后序数组长度为1时，说明是叶子节点，直接返回这个节点
    }
    const index = inorder.indexOf(rootVal);
    root.left = buildTree(preorder.slice(1, index + 1), inorder.slice(0, index)); // 根据左前序数组和左中序数组构建左子树
    root.right = buildTree(preorder.slice(index + 1), inorder.slice(index + 1)); // 根据右前序数组和右中序数组构建右子树
    return root;
};

分析：时间复杂度为 O(nlogn)，空间复杂度为 O(nlogn)。

收获

学会了使用中序遍历序列和后序遍历序列构造二叉树的方法，也能用同样的方法写出用前序遍历序列和中序遍历序列构造二叉树的代码。

至于前序遍历序列和后序遍历序列能不能构建出二叉树，答案是否定的，不能。因为没有中序遍历序列，就无法找到切割左右部分的位置，无法构建出唯一的二叉树。